還記得上一期討論的黑市買馬問題嗎?之前我們給出了一種解決方案,並將這道題目定性為錯題,但經過後續進一步地思考,筆者發現對於這道題的探索還遠沒有結束,如果在題幹中補齊一個前置條件,這將會是一道正確的題。
一、題目回顧
回顧一下原題:
在官方市場,有一匹馬的價格是500銅幣。玩家也可以前往黑市,黑市每次的入門費是20銅幣。每次進入黑市,都可能發生以下事件: (1)有1%的概率,以50銅幣購買一匹馬。 (2)有3%的概率,以100銅幣購買一匹馬。 (3)有X%的概率,以250銅幣購買一匹馬。 (4)有Y%的概率,獲得一枚碎片, 攢齊50枚碎片可以換一匹馬。 (5)有50%的概率,啥也沒有獲得。 假設市場信息暢通無阻,玩家知道這些信息。 問:如果希望黑市馬的期望價格與官方馬的價格相同,那麼事件(3)的發生概率X%應該是多少?
已經知道本問題的關鍵是事件(4),因為它的存在使得這個問題不再構成Markov Chain,在上篇文章我們按照大數定理求解,得到了一個結果為負的答案,但在驗證結果的過程中,o1模型提供了一個遞歸求解算法,並得出了一個正數答案。而上次由於短期無法驗證該答案的正確性,筆者並沒有再朝這個方向做進一步研究,文章發佈後,有讀者在評論區對該種方法給出了一些分析,那麼對這道題的研究就此結束了嗎?
後來經過筆者的進一步思考,發現o1給出的遞歸思想並不是筆者一開始想當然的那樣同解不同法,若按照此方法求解,我們將得到一個新的結果,並且明顯這個結果才是出題人所希望的。
二、遞歸算法

o1模型給出的遞歸思想
再來看一下 o1 給出的算法思想,既然無法把買馬過程看成一條鏈,那便把其按題目條件(4)拆分成 50 條構成 Markov process 且相互獨立的鏈,即玩家分別擁有 0 個碎片,1 個碎片,...,49 個碎片時再去買馬的情況。這 50 條獨立的鏈是可以按照全概率公式分別計算價格期望的,考慮有 k 個碎片時的買馬價格期望,只需將條件(4)轉換為 E(k+1),且當玩家擁有 49 玫碎片時,再去買馬對應的價格期望:
E(49)=47+5X
通過如下求解過程算出E(0)關於 Y 的函數:
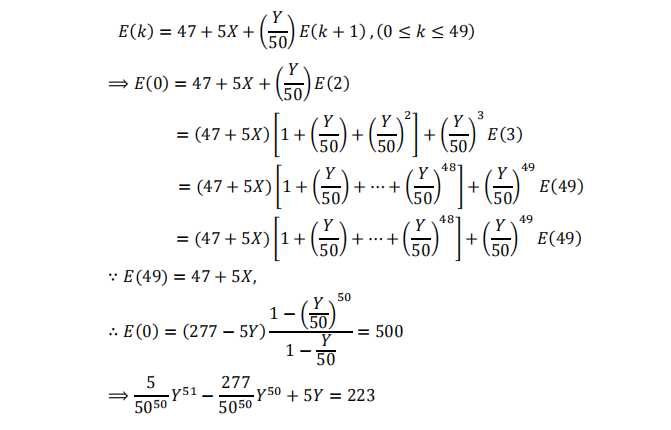
接著用二分法編程求解該代數方程,MATLAB代碼如下:
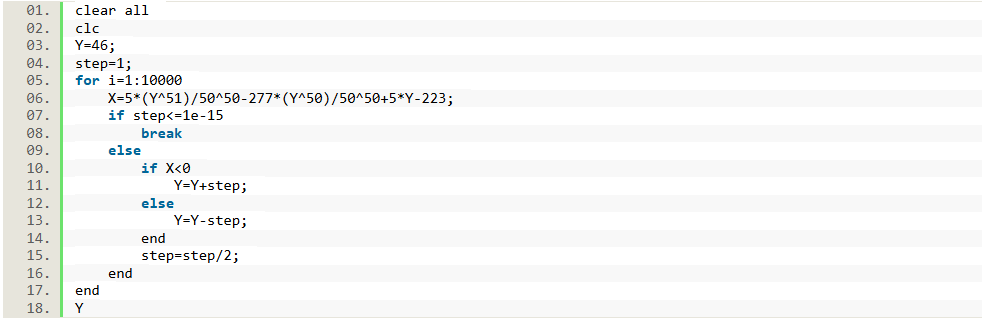
由上一篇文章結果可知,如方程有根則一定在 Y=46 附近,取初值 Y=46,代入後求解得 Y≈44.636998 ,在 46 附近變換初值,結果穩定,證明此時的 Y 確實是原方程的根,即在 X=1.36%,Y=44.64% 時,玩家在黑市購買第一匹馬的期望價格與正常價格相等。
三、結果分析
在此筆者想要強調的是,如果題目不對玩家買馬次數加以限制,那麼按照上一期的求解方法我們得到的期望價格是玩家買無窮匹馬時的極限情況,但本題微妙之處就在於此,如果只考慮玩家在黑市購買第一匹馬時的價格期望,那麼按照本文的遞歸算法同樣可以解出一個正確的答案,且符合實際。
試想現實中,如果有遊戲真的設計了這樣一個市場機制,那麼在活動剛上線被玩家一陣聲討後,一些玩家看到了筆者的分析文章,發現這竟然是一個穩賺不賠的購買系統,並分享到了遊戲論壇,使得不少玩家又紛紛參與其中,而後不少運氣好的玩家(混雜官方苟託)便會曬出自己省錢買馬的截圖,引得更多玩家下場參與。而設計這一切的遊戲策劃看著後臺飆升的銷量數據與風評逆轉盡收漁翁之利,既達到了本次活動的流水指標,又讓玩家心甘情願的充錢的同時直呼“良心”,真是大贏特贏。
最後,有了買第一匹馬的求解過程,感興趣的讀者可以再思考一下玩家買第二匹,第三匹,... ... ,第 n 匹馬時的期望價格,還可以畫一條曲線來觀察期望價格變化規律,這將使得本題更具現實意義與可移植性,如果有好的想法也歡迎在評論區分享出來。
