某玩家聲稱：
雖然已經大學畢業數年，但直覺告訴我不太對勁。眾所周知直覺往往不一定靠譜，所以還是科學論證一下。
由於該玩家統計時把野良一腳踢出了池子那我們也就當池子裡沒有野良。池子一共8個人形，除去野良是7個。那我們抽四個金，每個都是這七個人形之一的概率是100%。這句其實是廢話，但也是前提。
假設七種人形對應ABCDEFG。那我們每次抽取一共有7種可能性，4次抽取就是7的四次方2401種可能性。四次都是同一人形有7種排列組合即AAAA BBBB CCCC DDDD EEEE FFFF GGGG。概率為7/2401=1/343≈0.29%
那如果我們是歐皇，抽出4個不同人形的概率是多少呢。我們第一次抽的結果有七種不同情況，第二次抽要與第一次不同那有除去第一次抽取結果的6種情況，以此類推總排列組合為7*6*5*4=840種排列組合。概率為840/2401≈35%
為方便大家理解附上一張3選3的圖，7選3有840可能性，不太好示範
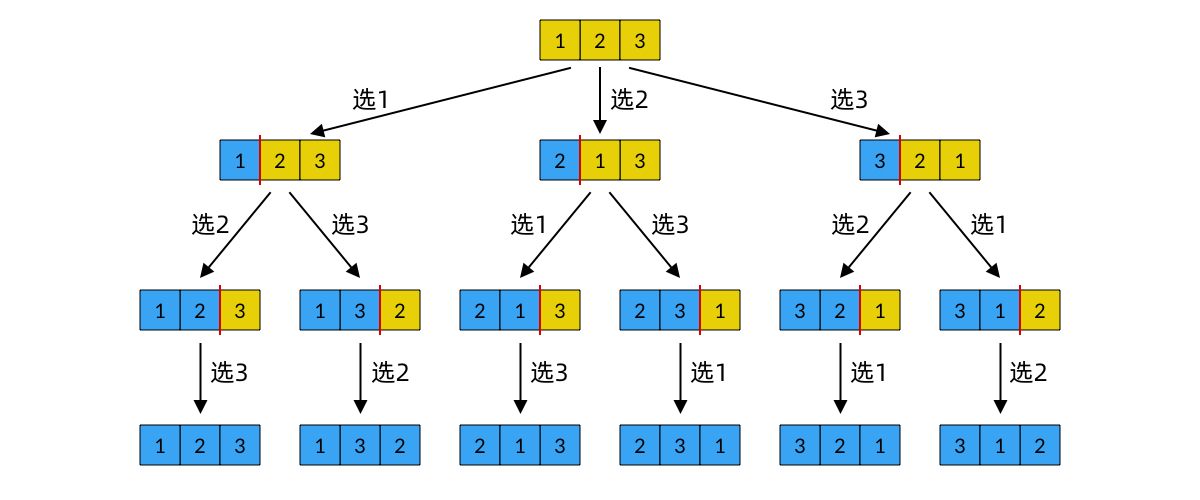
三選三的組合數為3*2*1=6
甚至我們可以將它寫成程序
public List<List<Integer>> permute(List<Integer> nums) {
List<Integer> current = new ArrayList<>(nums);
List<List<Integer>> res = new ArrayList<>();
backtrack(current, 0, res);
return res;
}
// current[0..m) 是已選集合， current[m..N) 是候選集合
void backtrack(List<Integer> current, int m, List<List<Integer>> res) {
if (m == current.size()) {
res.add(new ArrayList<>(current));
}
// 從候選集合中選擇
for (int i = m; i < current.size(); i++) {
// 選擇數字 current
Collections.swap(current, m, i);
// 注意：這裡傳入參數是 m+1，而不是 i+1
backtrack(current, m+1, res);
// 撤銷選擇
Collections.swap(current, m, i);
}
}
上面是給定一個不重複的數字集合，返回其所有可能的全排列程序範例。
單純學術交流，防止大家接受錯誤信息