我們先從一個簡單的問題入手。
在二維平面中有一個向量,它代表了我們生活在二維空間中的主角當下運動的狀態。向量的方向即運動方向,向量的大小即速度大小。如果我們不在於主角的移動速度,只是想得到他的運動方向,也就是我們常說的方向向量,我們該如何計算?
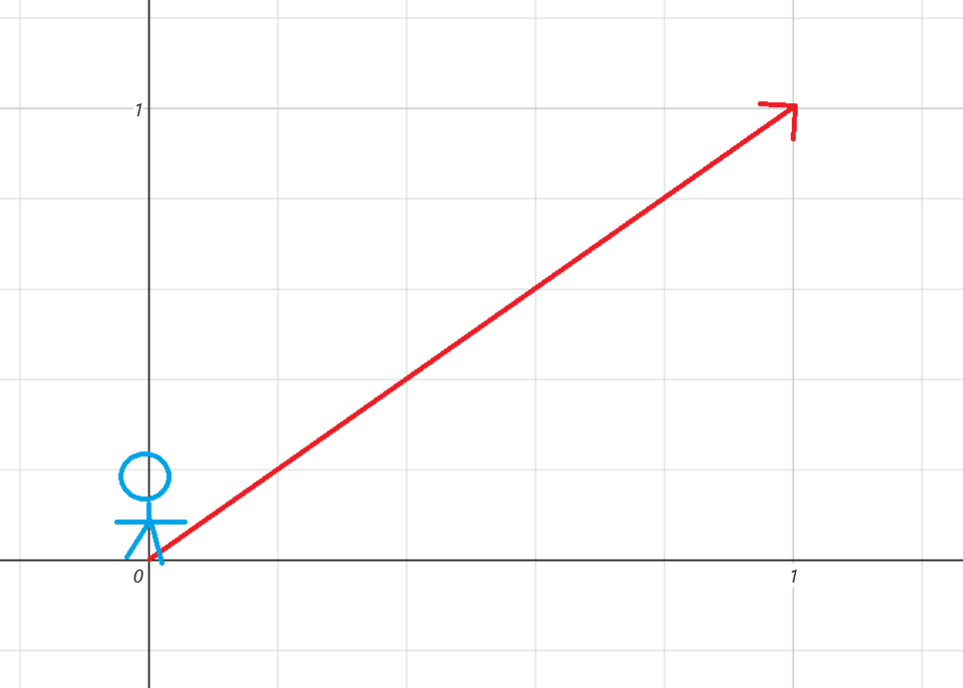
很簡單,我們利用勾股定理 a^2 + b^2 = c^2 即可求得向量長度的二次方,隨後我們再對結果做平方根運算,得到的值為向量的大小,最後我們再用原向量除以向量大小,得到的結果即為方向向量,這個計算方法通常被叫做歸一化(normalize),得到的向量我們也可以叫做單位向量。
方向向量不僅是在遊戲中的物理模擬非常重要,對於渲染來說也是一樣的。它能用來指明光線與三角面的方向,而方向則決定了光照程度、材質質感等關鍵效果的計算結果。
我們用簡單的式子來描述一下這個計算過程:V / ||V||,其中 V 為任意向量,||V|| 為向量大小。也就是說,我們只要得到一個向量大小的倒數,即 1 / ||V||,就可以快速計算出方向向量。而 ||V|| 又涉及到平方根操作,所以最終我們要計算的其實是平方根的倒數。
當然我們可以把倒數與平方根運算分開操作,但是在遊戲開發的蠻荒時代,平方根運算並不容易,倒數的操作也不是非常快速的簡單運算。被機能困在舊時代的開發者們渴望得到一個快速算法,能夠解決遊戲開發中涉及到的大量的平方根倒數運算。
那麼這個問題該怎麼解決呢?
牛頓的咒語
平方根該怎麼計算?當然你不能使用計算器。
舉個例子來說,我們就求 √2 吧。
我們可以做如下推導:
x = √2
=> x^2 = 2
=> 0 = x^2 - 2
所以我們可知,函數 f(x) = x^2 - 2 與 x 軸的交點即為 √2 的值,函數圖像如下:
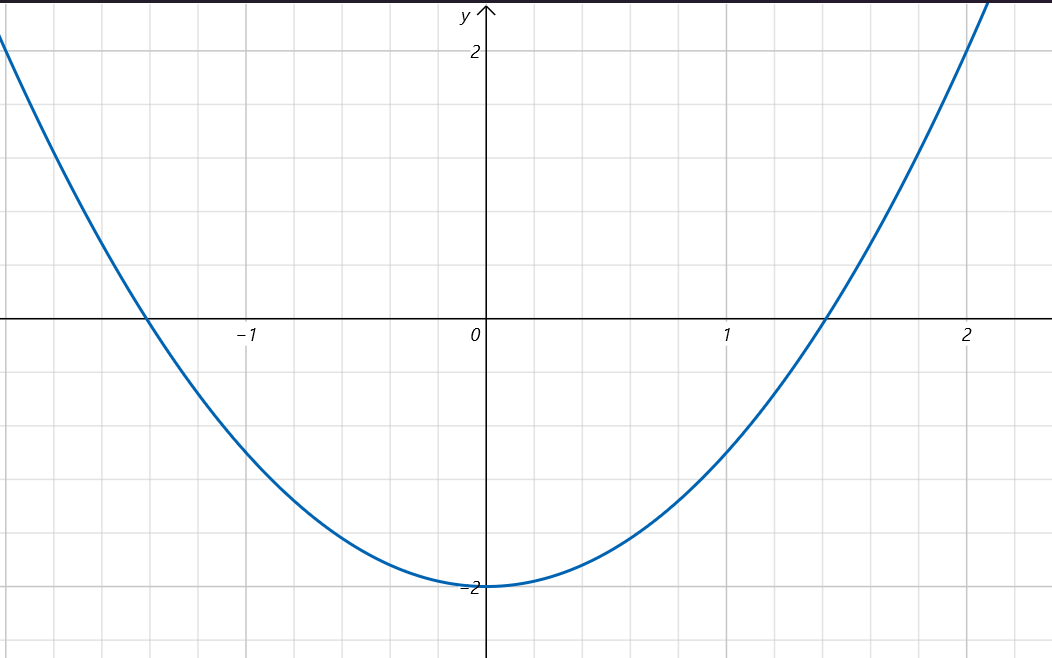
觀察圖像,我們可以推測這個值介於 1 與 1.5 之間。
上面的函數與方程只能讓我們得到 √2 這種形式的數值表達形式,那麼我們怎麼求得 √2 具體值呢?
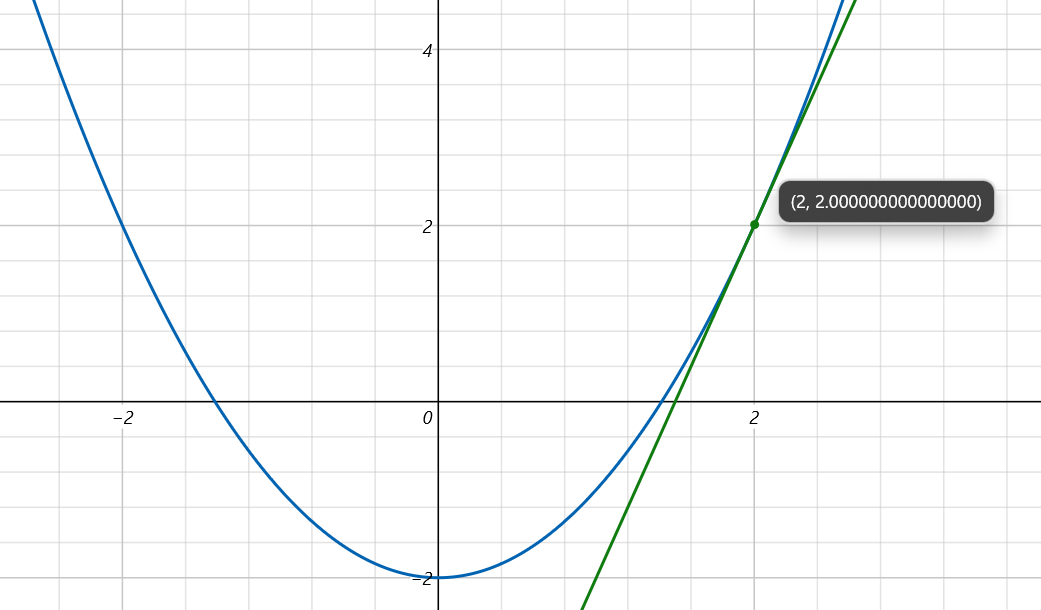
如上圖所示,我們畫一條線,這條線與函數 f(x) 的曲線相切於點(2,2),並且這條線與 x 軸的交點十分的接近我們要求得的那個點,這是一個好現象。也就是說,我們只要找出這條線的函數形式,並求得這條線與 x 軸的交點,我們就能的到一個 √2 的近似值。
那麼我們怎麼求得這條線的函數呢?
首先我們知道這條線經過點(2,2),那麼如果我們還能得到線的斜率,通過點斜式即可求得函數。
因為這條線本質上是函數 f(x) 在點(2,2)切線,所以它的斜率就是 f(x) 在這一點的導數。
所謂的函數的導數,它表示這個函數在某一點上變化的趨勢與程度。這一概念其實與經過切點的切線是保持一致的。切線的傾斜程度(即斜率)不就是代表了這條線上的值的變化程度嗎?
我們用 f '(x) 來表示函數 f(x) 的導函數,對於 f(x) = x^2 - 2 來說,f '(x) = 2x。
其實對於類似 f(x) = ax^n + b 這種形式的函數來說,導函數的形式非常簡單,就是 x 的指數減一,得到的值與 x 的係數相乘,偏移量 b 因為是常數,所以會被省略。按照這個規則,f(x) = ax^n + b 的導數就是 f ‘(x) = an * x^(n-1),所以 f(x) = x^2 - 2 導數即為 f '(x) = 2x。
我們將點(2,2)帶入函數 f '(x) = 2x 求得此處的導數為 4,即經過此處的切線的斜率為 4。
現在切線的斜率與切線經過的點都有了,帶入點斜式我們可得:
y - b = k(x - a);a,b 為函數圖像經過的點
y - 2 = 4(x - 2);
y = 4x - 6;
即切線函數為 g(x) = 4x - 6,並計算 0 = 4x - 6,所以切線與 x 軸的交點為(1.5, 0)。那麼我們要求的 √2 近似值即為1.5。
1.5 這個值明顯並不精確,它有點過於“近似”了。從圖上我們也能觀察到它與真正的 √2 的值還是有一定差距的。但是我們已經掌握了求近似值的方法,那麼我們是否可以重複上述過程,來進一步接近正確值呢?
答案當然是肯定的。我們已經得到了一個接近 √2 的值 1.5,那我們可以嘗試以這個值為基礎,再做一次上面的運算。
首先我們將 1.5 帶入 f(x),求得一個新的切點:
f(x) = x^2 - 2 = 1.5^2 - 2 = 0.25
新切點即為(1.5, 0.25)。
再導入導函數求切線斜率:
f '(x) = 2x = 2 * 1.5 = 3
最後帶入點斜式,得到切線函數:
y - b = k(x - a);
y - 0.25 = 3(x - 1.5);
y = 3x - 4.25;
3x = 4.25;
x ≈ 1.41666
我們也可以從圖像中觀察到這個結果:
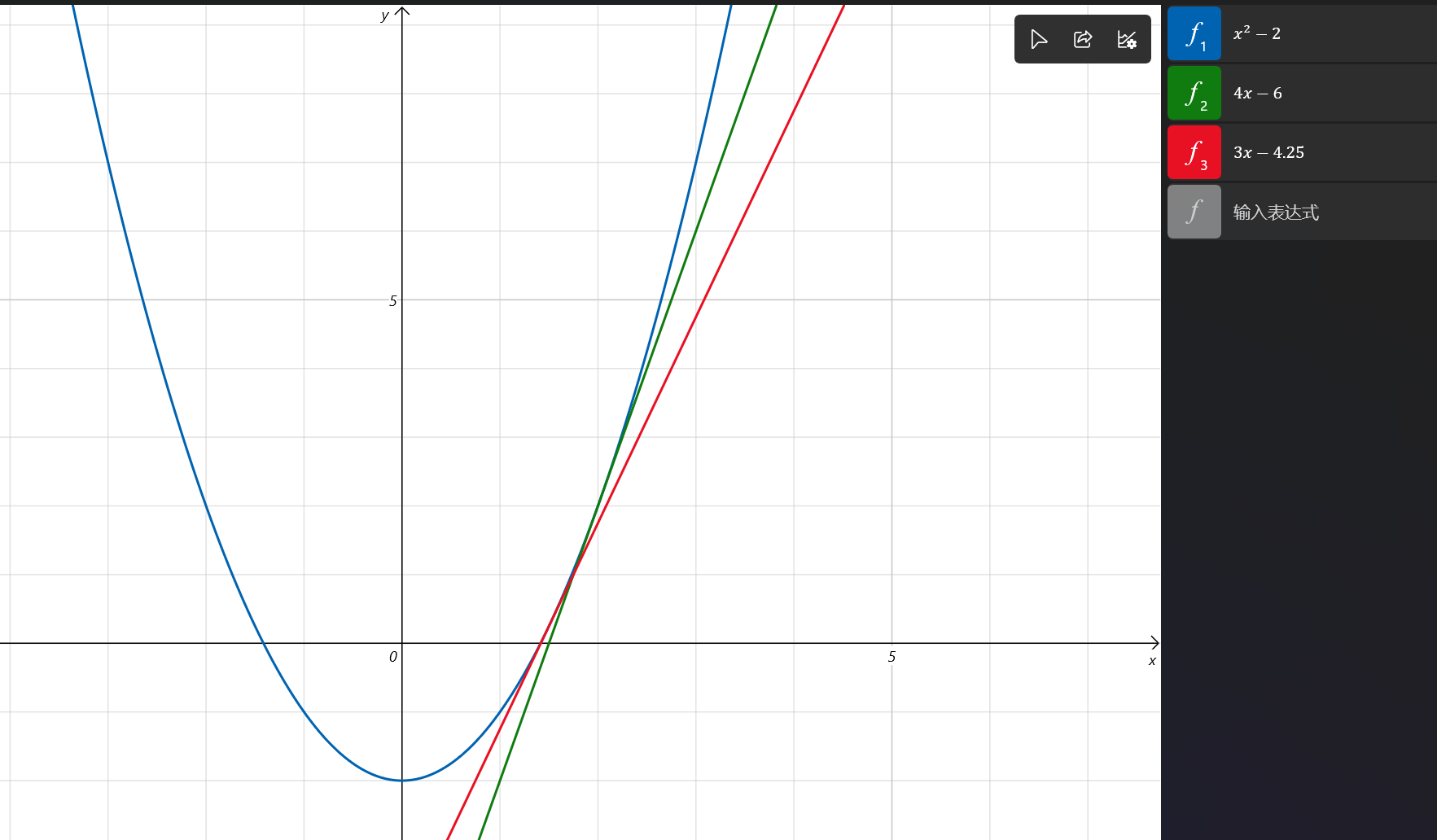
我們將這幾條線與 x 軸相交的部分放大觀察:
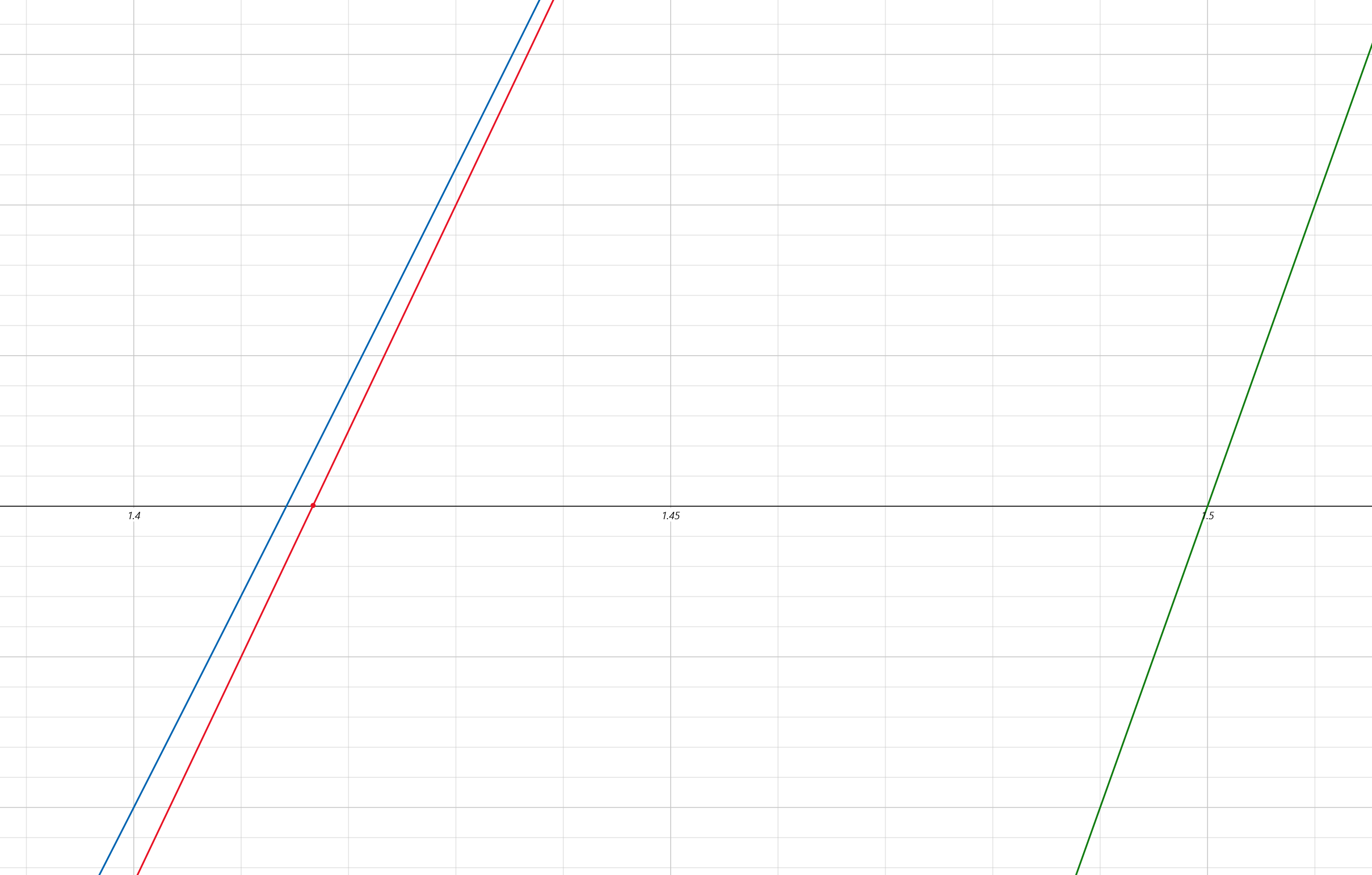
正如我們設想的那樣,運算的得到的結果作為下一次運算的初始值,遞歸運算下去,我們就能不斷的接近那個我們想要的值。
我們再從全局的角度觀察一下我們的計算的流程。我們有兩個關鍵函數,f(x) 和它的導函數 f '(x),用它們我們可以求得切點與斜率,再帶入點斜式求得切線函數,最後得到切線與 x 軸的交點,即為我們想要的值。從這個過程來看,我們好像可以總結出一個更簡單的公式,來表示這個計算過程,我們來嘗試一下。
點斜式 y - b = k(x - a),因為我們最後要求得的值為函數與 x 軸交點中的橫座標值,即點斜式中的 a 值;又因為 x 軸交點的縱座標必為 0,所以我們將點斜式變化為:
a = x - y/k
其中 x 與 y 組成我們當前已知的切點(例如上述第一次計算過程中的點 2,2),y 由 f(x) 計算得到,所以 y = f(x);k 為斜率,由導函數 f ’(x) 計算的到,所以 k = f ’(x)。
我們還知道 a 為我們要求得的最新的近似值,我們設它為Xn+1;x 為我們當前已經求得的近似值,我們設它為Xn。
將上述各個值的轉換導入式子,我們可得:
Xn+1 = Xn - f(Xn) / f '(Xn);
帶入具體的實例測試一下?
第一個切點我們選(2,2),並且我們有 f(x) = x^2 - 2,f '(x) = 2x,帶入公式即為:
Xn+1 = 2 - (2^2 - 2)/(2*2) = 2 - 1/2 = 1.5。
恭喜!我們又一次發明了牛頓的咒語:牛頓迭代法。
在這個過程中,我們不難發現牛頓靈活的運用了近似值這個概念,以近似值的方式,不斷逼近精確值。與其說是算法, 不如說是一種策略。
對於這條所謂的咒語來說,它不僅簡單,而且還特別適合用代碼實現,我們可以用 for 或 while 為循環計算提供動力,直到計算出我們想要的精度,一次平方根計算就完成了。
但是,我們開頭也提到過,這是一個蠻荒的時代,計算機的算力有限,而我們要完成的卻有很多,我們很難使用一個依賴循環次數得到確切值的算法。循環就像一個吞噬算力的猛獸,它很快就會讓機器的計算能力變得捉襟見肘。
如果只需要念一次咒語就好了。
沒錯,只進行一次牛頓迭代法。不是不可能,只不過需要我們首次提供的 Xn 就足夠精確罷了,足夠精確的 Xn 得到更精確的 Xn+1。
這好像是個死循環。
如果卡馬克的魔法沒有誕生的話。
卡馬克的魔法
假設我們有一個數字,30000,用科學計數法表示它即為,3 * 10^4。不難發現 10 的指數其實就是數值中 0 的個數。
十進制的規則深入我們的骨髓,其中的道理也無需多言。
那麼二進制呢?
假設我們有一個二進制數 10000(十進制值為 16),我們類比上面的十進制規則,那麼二進制 10000 的科學計數法表示形式即為 1 * 2^4。此處與十進制不同的是,二進制是以 2 為底的指數形式。你可以仔細品味一下乘法的本質,再從十進制類比到二進制。
這一切都說得通,而且非常自然。
我們再進一步。
十進制數 31000,用科學計數法表示即為 3.1 * 10^4,觀察這個表達形式,我們不難發現,10 的指數本質其實是在表明小數點的移動位數。
那麼類比到二進制中,二進制數 11000 (十進制值為 24)的科學計數法表達形式即為 1.1 * 2^4,符合我們上面觀察到的規律。
這就是二進制的位移規則。
接著我們再來複習一下浮點數編碼規則。

如上圖所示,浮點數在計算機中的二進制存儲模式被分為三個部分,首位是符號位,用來標識數字的正負號;後八位是偏執指數位,用來表示在科學計數法下小數點偏移的位數;最後的二十三為則表示在科學計數法下,小數點後面的數字排列,這部分融合了原數字的整數與小數兩個部分。
我們以一個具體的數字來舉例,二進制 111 的科學計數法表達形式為:
1.11 * 2^2
以浮點數編碼規則編碼後,在計算機中的二進制形式為:

其中指數位的計算規則是,小數點偏移量 + 127。以 111 為例,科學計數法表達後小數點向左偏移兩位,所以指數位為 2 + 127 = 129,二進制表達即為 10000001。
至於尾數位,因為二進制科學計數法的規則就是小數點會停留在首個不為 0 的位數後面,所以我們只需要去掉科學計數法中的“1.”,剩下的部分就是尾數位的本體。
以上就是我們對浮點數編碼規則的理解。
關於浮點數,我們前面所討論的一直都是科學計數法到浮點數二進制形式的轉換,那我們就忍不住好奇,將這個過程反過來呢?浮點數二進制形式如何轉化為科學計數法呢?
很簡單,對於偏置指數位來說,我們只需要用偏執指數位 - 127,結果就是科學計數法中的小數點偏移量,就上述中的例子來說:
100000001 - 01111111
= 129 - 127
= 2
對於尾數位來說,反向推到科學計數法的表達形式時,需要在尾數位前面加上“1.”,就上述中的例子來說,也就是在 “11000……” 前面加上 “1.”,即 1.11,0 被省略。
這還不夠,根據上面的文字描述,我們可以試著總結出一條公式。
我們設尾數位為 M,因為尾數位共 23 位,尾數位反推至科學計數法時,小數點要出現在尾數位形式之前,那麼根據我們前面提到的二進制位移規則,尾數位小數點向左移動 23 位,即 M / 2^23,最後別忘了,我們還要加上一個“1.”,所以最終公式應該為:1 + M / 2^23;

接著我們設偏置指數位為E,則科學計數法中小數點偏移量的計算為:E - 127。
結合尾數位部分的公式,我們可以得到(這裡我們省略的符號位,因為加入符號位很簡單,而且後續我們的討論也不需要符號位):
科學計數法表達形式 = (1 + M / 2^23) * 2^(E - 127)
對比一下例子中的科學計數法表達:1.11 * 2^2
那麼這個公式有什麼用呢?我們先來隨意擺弄一下它看看會發生什麼。
因為公式很明顯被乘法分為兩個部分,並且其中一部分還是 2^(E - 127) 這種 2 的指數形式,那麼我們不防試試對數?
對數的運算法則很有意思:
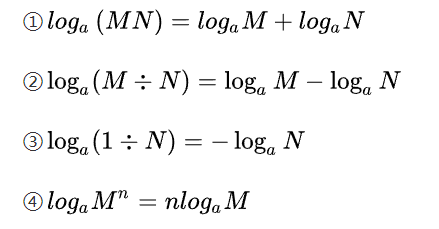
它能將乘法的兩部分,變為加法(第一條);還能將指數轉變為乘法(第四條)。這兩條都存在於我們的公式之中,那我們就來試試。
設 a = (1 + M / 2^23) * 2^(E - 127),我們對兩邊都進行以 2 為底的對數運算,可得:
㏒₂a = ㏒₂((1 + M / 2^23) * 2^(E - 127))
㏒₂a = ㏒₂(1 + M / 2^23) + ㏒₂2^(E - 127)
㏒₂a = ㏒₂(1 + M / 2^23) + ㏒₂2 * E - 127
㏒₂a = ㏒₂(1 + M / 2^23) + E - 127
唉?有趣,2 的指數形式消失了,只剩下 E - 127,從某種角度來說,整體運算變得簡單了。那 ㏒₂(1 + M / 2^23) 部分呢?
我們知道 M 作為尾數位的二進制形式,具體二進制取決於我們浮點數的具體數值,所以這裡可以把它看做是一個變量,M / 2^23 自然也是隨著 M 的變化而變化的,我們不防暫時先將他們看做一個整體 x。於是 ㏒₂(1 + M / 2^23) 就變成了 ㏒₂(1 + x)。這就又簡化了我們的式子,因為 ㏒₂x 本身就是一個很常見的對數函數,圖像如下:
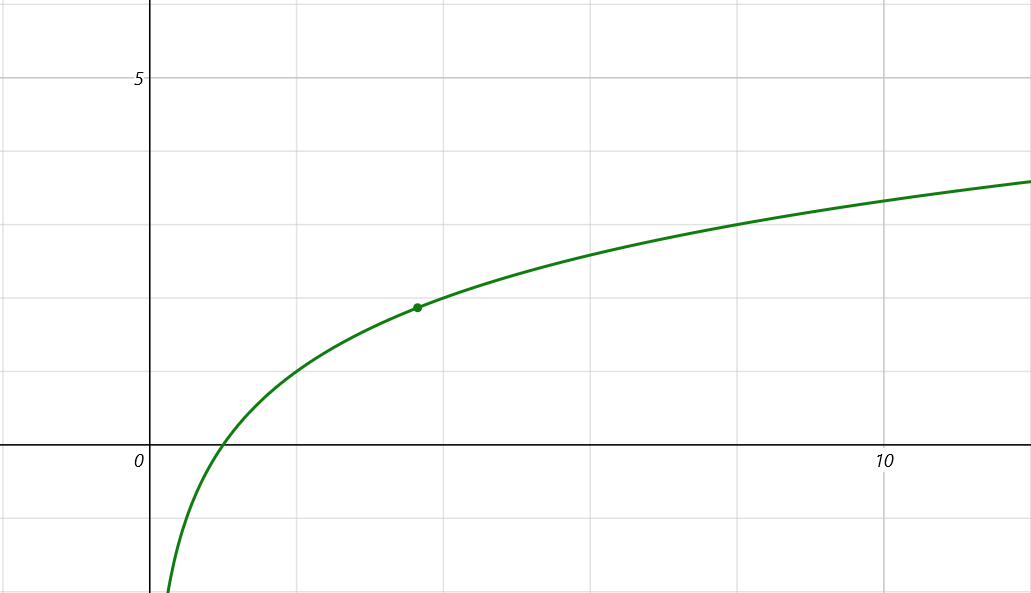
而 ㏒₂(1 + x) 只需對圖中圖像稍作位移:
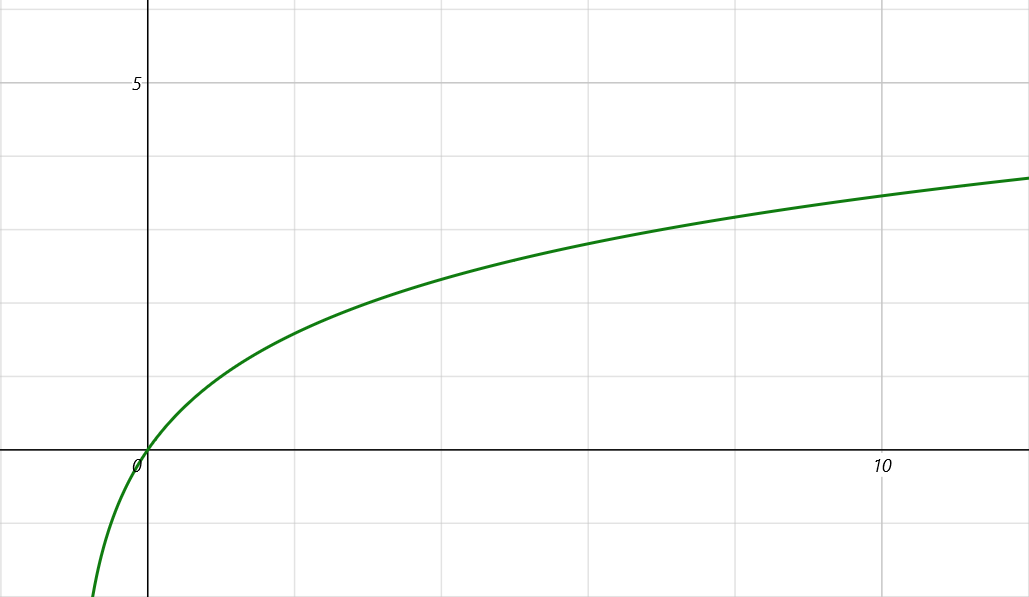
這還沒完,因為我們知道 M / 2^23 必然大於 0 小於 1,所以 ㏒₂(1 + x) 中,x 的取值範圍也在 0 至 1 之間,那麼我們放大這個圖像的細節到 x 的 0 至 1 區間:
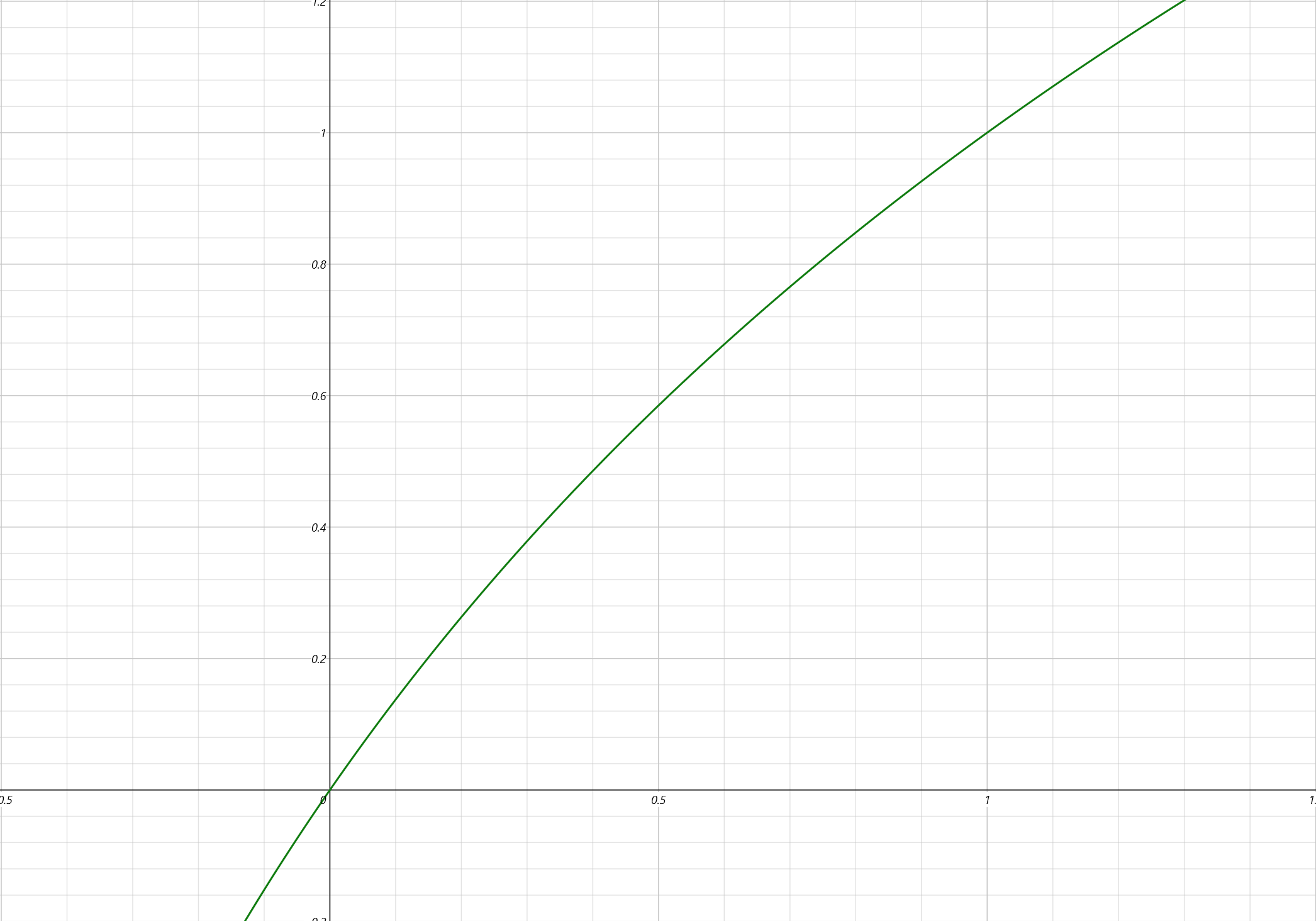
從圖像中可以看到,這條曲線在 0 到 1 之間的部分,其實近乎於直線,再回想一下我們從牛頓的咒語中學到了什麼?
沒錯,近似值。在我們實際的工程應用中,很多數值都不是十分精確的,或者說對數值的精確度要求是變化的。所以既然它接近於一條支線,那我們為什麼不就把它當做一條支線呢?
因為曲線經過點原點與點(1,1),所以我們可以把它看做 y = x:
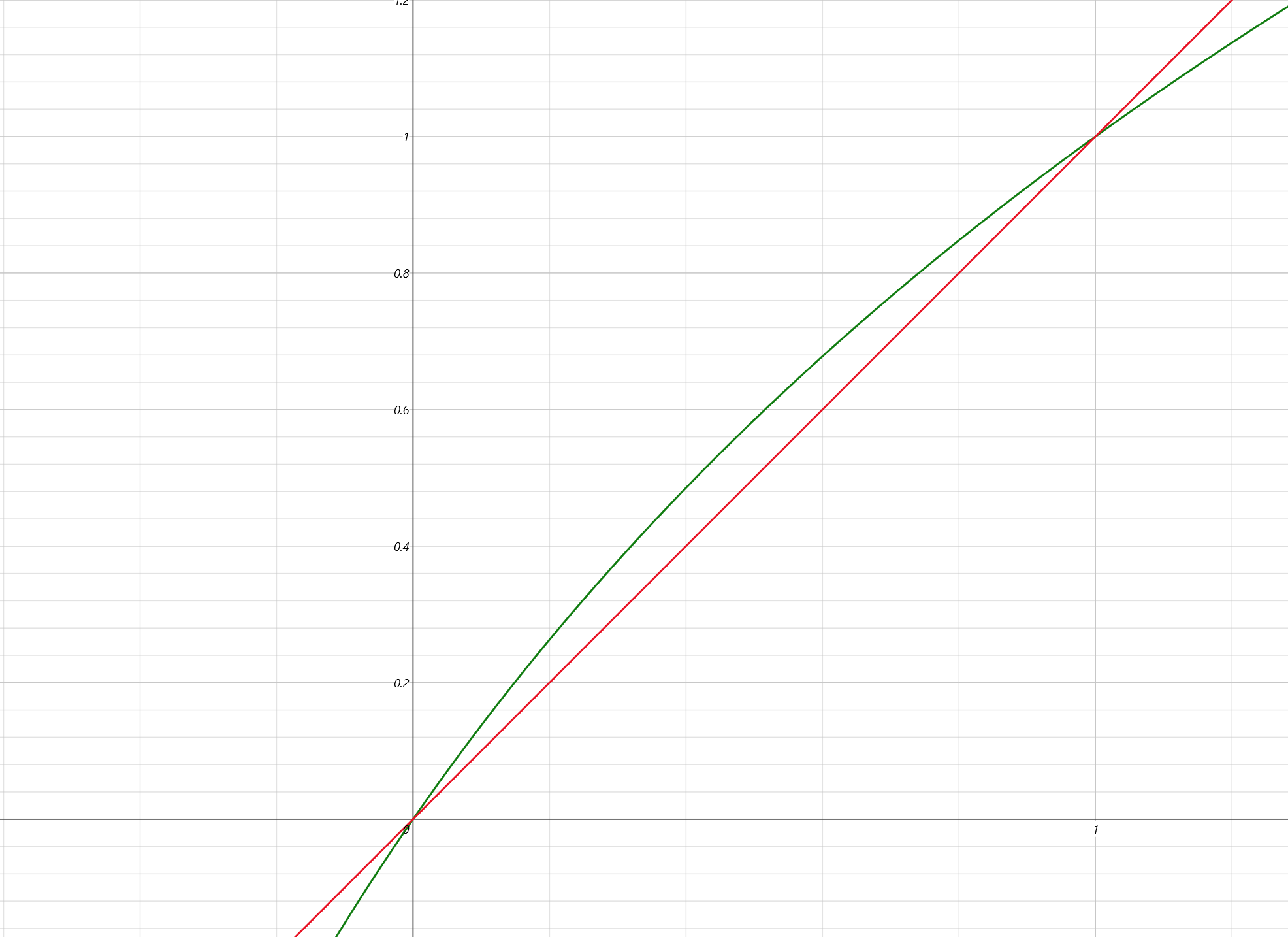
從圖上可以觀察到,y = x 與 ㏒₂(1 + x) 在 0 至 1 區間的值,真的非常相近。
那麼,因為:
㏒₂(1 + M / 2^23) ≈ M / 2^23
所以:
㏒₂a = ㏒₂(1 + M / 2^23) + E - 127
≈ M / 2^23 + E - 127
到這裡還不夠,我們再稍作變形,將 M / 2^23 + E - 127 中 M / 2^23 + E 提取 1 / 2^23 可得:
1 / 2^23 * (M + E * 2^23) - 127
最後我們終於來到了這裡。
觀察式子中的 M + E * 2^23,你看它像什麼?
還是 1.11 * 2^2 的二進制形式為例,它的二進制形式為:

其中,M = 11000000000000000000000;
E = 10000001;
那麼,E * 2^23 根據二進制位移規則,就是將小數點向右移動 23 位,就是說要在 E 後面添加 23 個 0:
E * 2^23 = 10000001 00000000000000000000000;
於是可得:
M + E * 2^23
=
11000000000000000000000
+
10000001 00000000000000000000000
=
10000001 11000000000000000000000
原來,M + E * 2^23 就是這個 M 和 E 所代表的那個數字的二進制形式。
那麼根據我們的推導過程:
㏒₂a = ㏒₂(1 + M / 2^23) + E - 127
≈ M / 2^23 + E - 127
= 1 / 2^23 * (M + E * 2^23) - 127
我們可以得到一個結論:
對於數字 a,設 A 為浮點數 a 二進制形式,那麼:
㏒₂a ≈ 1 / 2^23 * A - 127
也就是說我們得到了一個快速計算對數的算法,只要利用浮點數二進制就可以快速計算。
還記得我們最開始的目的嗎?我們是為了計算平方根倒數,那這個快速計算對數的方法和平方根倒數計算又有什麼關係呢?彆著急,我們接著來。
我們設 a 的平方根倒數,即 1/√a ,為 y,那麼我們有:
㏒₂y = ㏒₂a^(-1/2)
= -1/2 * ㏒₂a = -1/2 * ((1 / 2^23) * A - 127)
也就是說:
㏒₂y = -1/2 * ((1 / 2^23) * A - 127)
y 雖然是 1/√a 的符號表現,但是,y 最終一定有一個值對不對?它既然是一個值,那就必然可以表達為浮點數的二進制形式,我們就設浮點數 y 的二進制形式為 Y。這個時候我們就可以 ㏒₂y 也轉化為二進制快速計算對數的形式:
㏒₂y = (1 / 2^23) * Y - 127
而 Y 是浮點數 y 的二進制形式,也就代表了 y 的值,即 1/√a,也就是我們想要求得的 a 的平方根倒數。
終於,一切都說的通了:
(1 / 2^23) * Y - 127 = -1/2 * ((1 / 2^23) * A - 127)
Y = 381 * 2^22 - 1/2 * A
Y = 1598029824 - 1/2 * A
如果我們用符號 “>>” 表示二進制向右的移動,那麼考慮到我們前面所提到的二進制位移規則, 1/2 * A 就等同於 A >> 1,它表示將二進制 A 向右移動一位;如果我們將 1598029824 轉化為十六進制,那麼最終的式子就變為:
Y = 5F400000 - A >> 1
根據最終我們得到得的這個式子,我們得出一個結論:
將浮點數 a 的二進制形式所代表的值乘以0.5,再與數值 1598029824 作差,結果的絕對值即為 A 的平方根倒數。
這就是卡馬克在雷神之錘 3 中所寫下的快速平方根倒數算法。它巧妙的將浮點數的編碼規則與平方根倒數的計算相結合,一切都顯得如此自然又彷彿是巧合。
我們看一下具體的代碼實現:
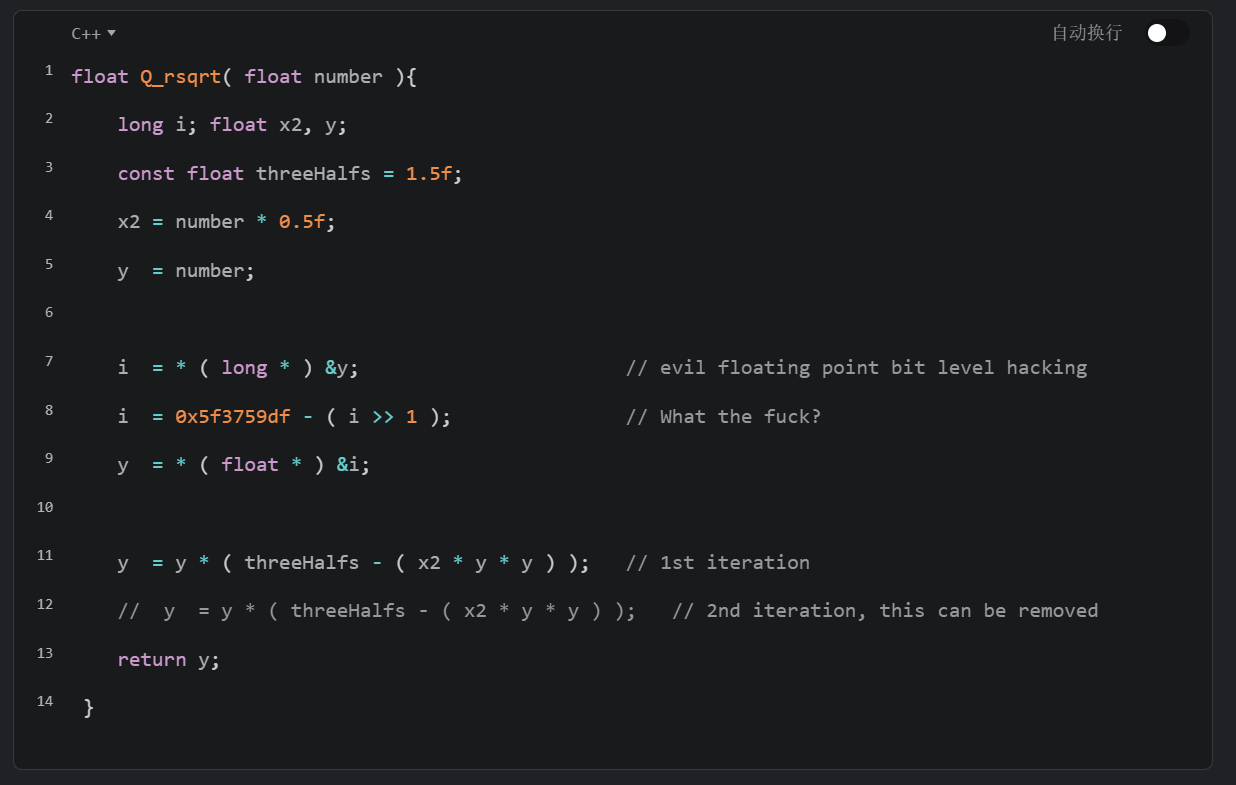
其中第七行代碼,先將 y 值轉化為 long 型,因為整型的編碼就是簡單的二進制與十進制的轉換,不涉及類似於浮點數編碼規則對二進制數的特別解讀,所以轉化為 long 型,就相當於是原封不動的保存了浮點數 y 的二進制。
第八行代碼與我們上面推導出的 Y = 5F400000 - A >> 1 相似,不同的點在於減數,代碼中的減數 0x5f3759df 看起來比我們的 5F400000 要更加精確。這也是事實,還記得我們上面提到過的 y = x 與 ㏒₂(1 + x) 在 0 至 1 區間的圖像對比嗎?

我們能看到,雖然兩個函數的圖像在 0 至 1 區間內相似,但是歸根結底還是不同的,然而我們的所有推導,都是建立在他們非常相似的基礎上,它們越相似,我們的誤差就越小,算法的精度就越高。如果我們將 y = x 變為 y = x + 0.05,則圖像如下:
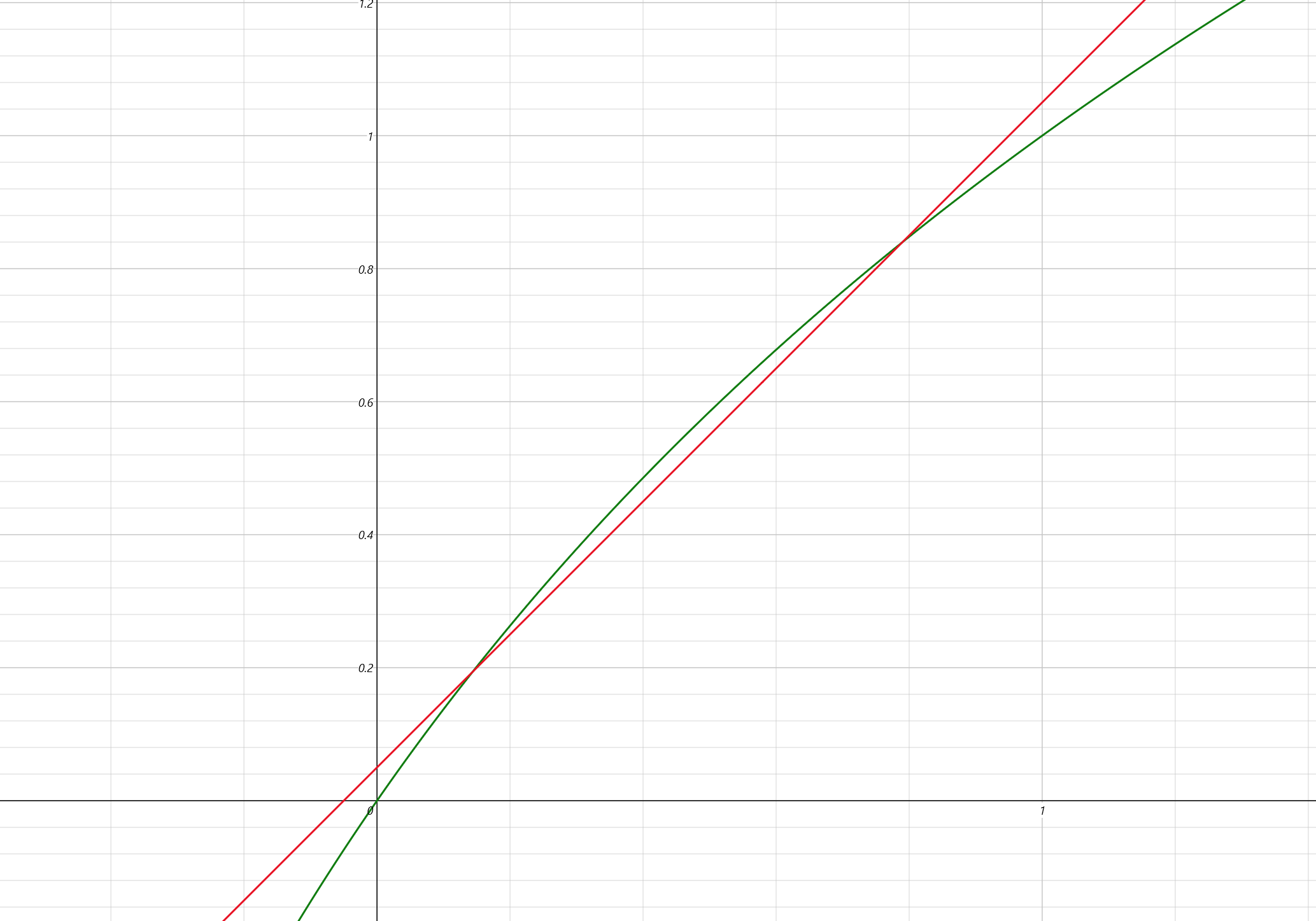
這個 0.05 我們可以叫做修正值。這個修正值在我們的計算過程中,最終會以常數的形式與 5F400000 相加,實際代碼中的 0x5f3759df 就是這麼來的。這個修正值可以按照一定的策略來做嘗試,比如我們可以使用二分法,快速縮減嘗試範圍,最紅確定一個相對精確的修正值。
最後第十一行代碼,使用了牛頓迭代法進一精確我們得到的數值。具體代碼的邏輯為:
Y = 1/√x
=> Y^2 = 1/x
=> 1/Y^2 - x = 0
即,我們有函數 f(Y) = 1/Y^2 - x,此函數當 x 為 0 時的圖像如下:
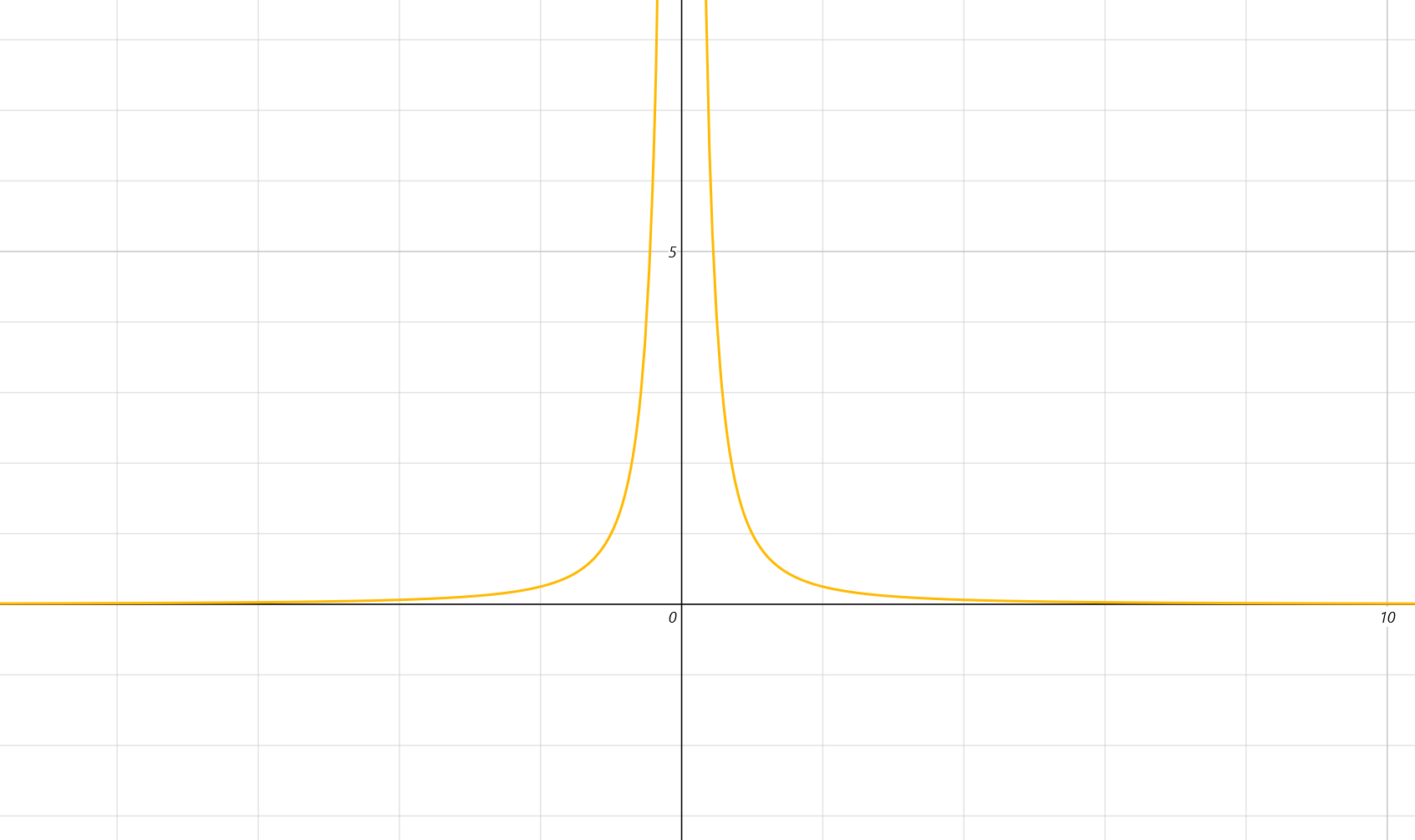
由圖可知,當 x = 0 時,函數圖像無限接近 x 軸,但並不與 x 軸相交;如果 x >= 0,我們可以想象,函數圖像會向下位移,之後與 x 軸相交處,即是我們要求得的 x 的平方根倒數。
因為 x 是我們想要求得平方根倒數的目標數值,所以對於每次計算來說,這都是一個常數,那麼根據牛頓迭代法可得:
已知,f '(Y) = -2/Y^3
所以,
Yn+1 = Yn - f(Yn) / f '(Yn)
=> Yn - (1/Yn^2 - x) / (-2/Y^3)
=> Yn * (3/2 - x/2 * Yn^2)
此式子就對應代碼中:
y = y * ( threeHalfs - ( x2 * y * y ) );
這與我們在牛頓的魔法一節最後提到的,以一個相對精確值得到更精確值的目標相對應。
最後值得一說的是,其實這個快速計算平方根倒數的算法並非出自卡馬克之手,不然卡馬克的註釋也不會是 WTF?了。
對於這個算法最初的發明者,我們可以參考 wiki 上的說法:
威廉·卡漢 (William Kahan) 和 K.C. 伯克利分校的 Ng 於 1986 年 5 月寫了一篇未發表的論文,描述瞭如何通過使用比特微調技術(bit-fiddling techniques)和牛頓迭代法來計算平方根。 20 世紀 80 年代末,Ardent Computer 的 Cleve Moler 瞭解了這項技術,並將其傳授給了他的同事 Greg Walsh。 Greg Walsh 設計了現在著名的常數和快速反平方根算法。 Gary Tarolli 正在為 Kubota(該公司當時為 Ardent 提供資金)提供諮詢,並可能在 1994 年左右將該算法引入 3dfx Interactive Jim Blinn 在 1997 年 IEEE 計算機圖形和應用專欄中演示了平方根倒數的簡單近似值計算。對其他當代 3D 視頻遊戲的逆向工程中,發現了動視 1997 年 Interstate '76 中算法的變體。 Quake III Arena 是一款第一人稱射擊遊戲,由 id Software 於 1999 年發佈,並使用了該算法。 Brian Hook 可能將 3dfx 的算法引入了 id Software。2000 年,中國開發者論壇 CSDN 上出現了對該代碼的討論,Usenet 和 gamedev.net 論壇於 2002 年和 2003 年廣泛傳播了該代碼。人們開始猜測誰編寫了該算法以及該常數是如何導出的。 有些人猜測是約翰·卡馬克。Quake III 的完整源代碼在 QuakeCon 2005 上發佈,但沒有提供答案。 2006 年,當 Greg Walsh 聯繫 Beyond3D 時,作者身份問題得到了解答,因為他們的猜測在 Slashdot 上廣受歡迎。 2007 年,該算法在一些使用現場可編程門陣列 (FPGA) 的專用硬件頂點著色器中實現。