——基于游戏《幸福工厂》机械产能的思考
前言:这不是一篇结论性文章,更不可能是一篇论文,这仅是一篇来自普通玩家在游戏过程中产生的思考及其记录。
《幸福工厂》是由Coffeestain Studio于2019年发行的一款工厂管理模拟游戏
(太空i电梯——游戏内截图)
游戏最大的特点就是可以通过建设全自动生产线来解放双手实现“材料自由”,因此这是一款十分休闲不需要思考太多的游戏(?)在体验了几天后,引起了我的一些思考。
对于一条生产线来说,不同材料的原料和产率是一个需要提前考虑的问题。对于最基础的材料——铁锭——只要找到一口铁矿就能生产,在不进行超频生产(即使用特殊材料提高该机械的生产量,耗电量、原料耗费也会同步提高)的情况下,一台冶炼机的产率是30铁锭/min,同时消耗30铁矿(1:1)。以纯净铁矿(纯净度会影响矿机的产量)为例,一台一级矿机就可以同时为4台冶炼机提供铁矿,而且都是100%效率(不会有产能过剩和原料不足的情况)。铁锭的下一级产物是铁棒和铁板,产率是15铁棒/min耗费15铁锭/min和20铁板/min耗费30铁锭/min,值得注意的地方是,铁板的原料和产物比例并不是1:1而是3:2,在游戏中这样原料和产物比不是1:1的材料有很多。这就导致了在生产线中,如果要保证每台机械的效率都是100%,那各生产机械之间就并不只是一对一的关系,可能还会有一对多和多对多的关系。下面用我的一条转子生产线来举例说明这个问题:
首先来看转子的配方和产率:
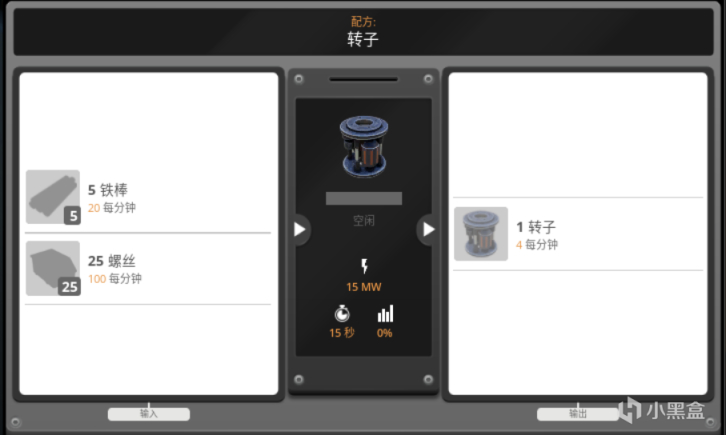
转子
在不超频的情况下,每分钟生产4个转子,耗费20铁棒和100螺丝,而螺丝产率为60/min耗费10铁棒/min。也就是说如果搭建一条转子产线,使用120铁矿/min的矿机,可以得出该公式:
120铁矿=8转子+20铁棒+40螺丝
也就是说如果按照这个公式搭建的生产线在100%效率的情况下每分钟不仅可以生产4转子,还可以积累40螺丝和20铁棒,一举多得
理论计算完之后就需要画出实现的线路图了:

由于这个游戏不能随意控制传送带的传输速率,所以使用分离器(把一条传送带平分二等分或三等分)和合并器(把最多三条传送带合为一条)达到控制各生产机械输入量的目的,但是这种方法会出现一种问题,这在后面会提到。
这套生产线里的每一台机器的效率都是100%,并且沿中间的仓库轴对称(强迫症狂喜),左右两边独立工作互不影响,上下两层可以共用同一个仓库(垂直对齐)
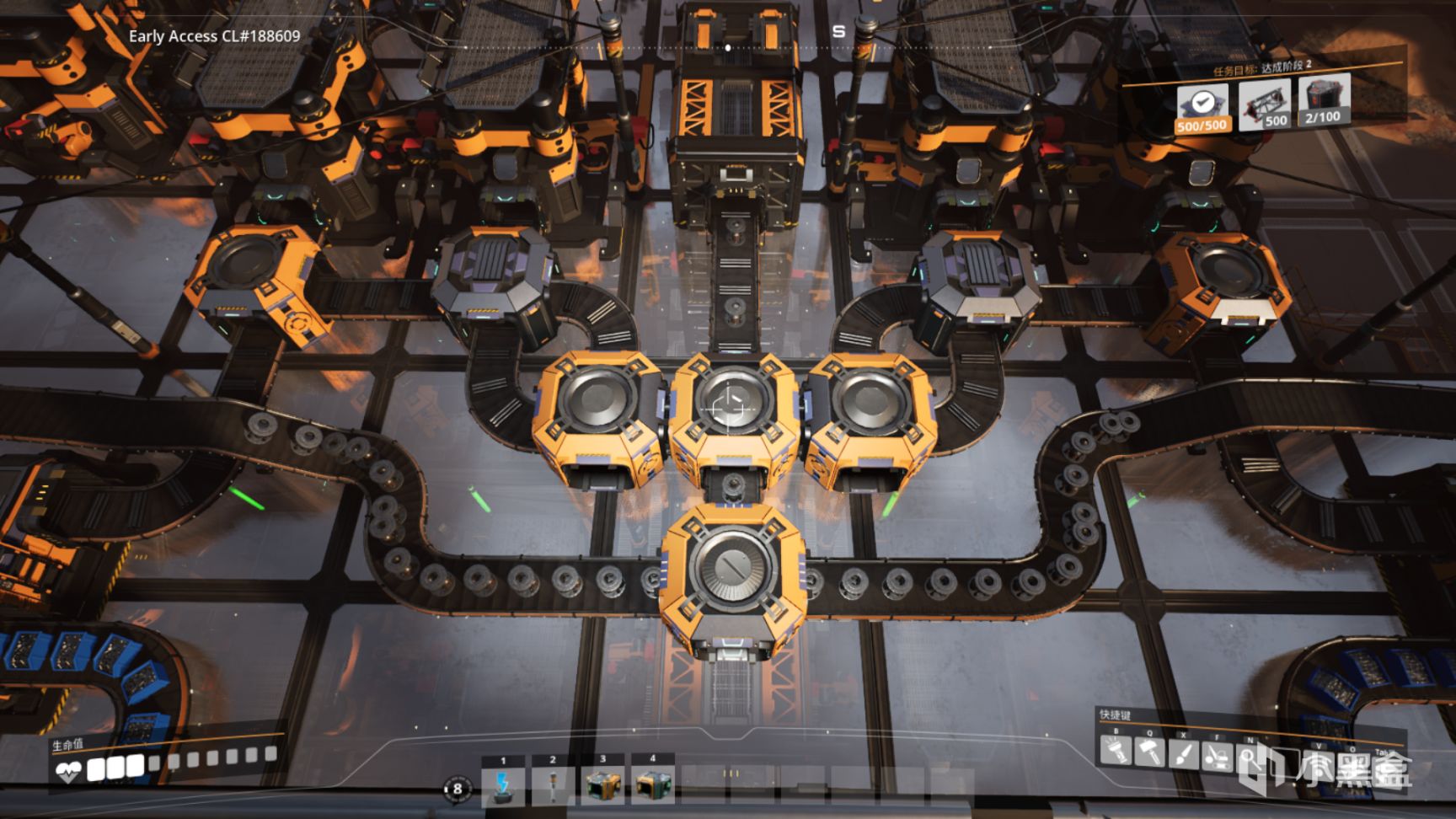
完全对称
产线部分截图
这套生产线在设计和实现时都没有遇到什么问题,唯一一点引起我注意的,就是感觉这种设计思路有种莫名的熟悉,但也说不上具体是什么思路。
在完成了转子生产线的建设后,我发现还缺少一条模块化框架的生产线,于是我打算如法炮制出一条仍旧以全机器满效率为设计思路的模块化框架产线,但这次就没有这么容易了。
首先是这个十分恶心人的初始配方:

铁棒的产量在不超频下是15/min,而加强板是5/min耗费30铁板、60螺丝/min,怎么看都对不上。只能是取他们的倍数,输入x3、输出x5也就是:
15加强板+60铁棒=10模块化框架
换算成铁矿就是:
240铁矿=10模块化框架
二级矿机纯净矿刚好是240铁矿/min,需要8台冶炼机,好嘛,工程量还挺大
还是一样,先计算一下分配情况:
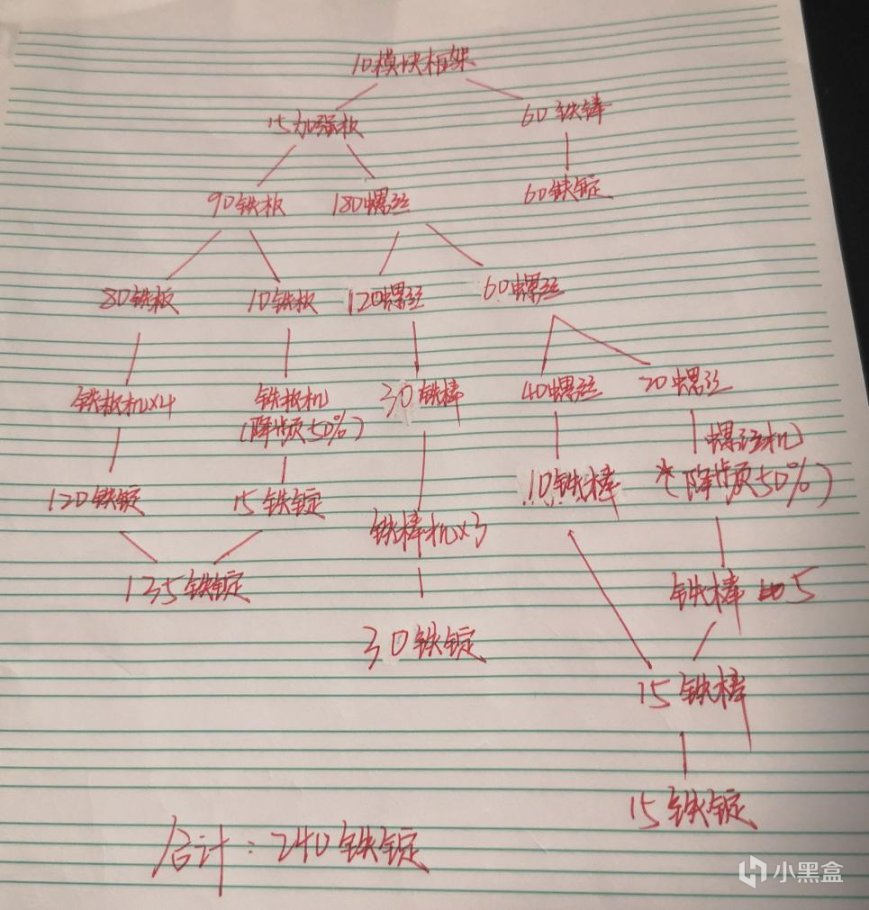
这计算起来就没有转子线那么简单了,还需要把两台机器降频(和超频相对),不过最起码第一步理论证明部分通过了。
接下来是流程图环节:
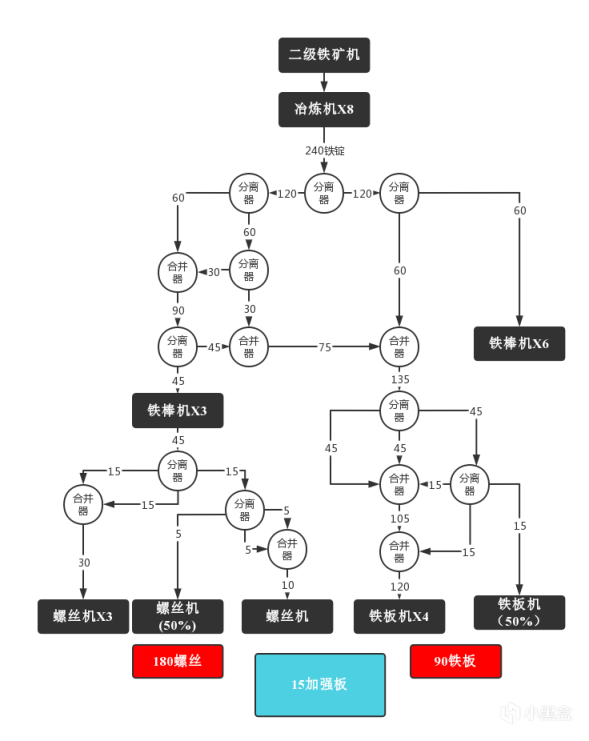
分离的过程还是比较曲折的,正当我准备把加强板和铁棒对接以完成最后的搭建时,一个致命的问题出现了,就是我在上面提到的,由于这个游戏不能随意控制传送带传输速率,因此采用合并器和分离器这种“曲线救国”的方式。现在,我只需要把60个铁棒分成5等分即每份12,再送到5台构造机里就可以完成这条产线的搭建,这听起来很简单不是吗?但是,我要怎么在只能除2或3且不能进行减法的情况下,把60分成5等分?很明显,通过分离器的拆分以及合并器的组合并不能实现这个需求,并且对于15个加强板,也无法将其分成5等分。这种通过调整输入速率以保证满效率的方法,最终在实现的时候会暴露出局限性——无法应对所有的数值。
那接下来怎么办?将模块框架的产量削减为8?还是增加铁棒和加强板的产量?无论前者后者都会违背效率至上的初心,但是从这个公式上来看,对于整体来说,240铁锭确实是可以不差毫厘的生产10个模块化组件的,所以就着整体性的方向,我想到了下面这种办法:

较远机器的效率会逐步提高
通过逐个输入,可以使靠前的机器的在刚运作时就具有较高的效率,而在第一台机器快要输入过剩时,多余的材料会被送到下一台机器以提高其效率。也就是说,当这套生产线启动时,有一部分的机器在刚开始时没有达到满效率,但在启动一段时间后,也就是积累了一定的原料后,所有的机器都能达到满效率,并且会一直维持满效率。而效率最低的机器达到满效率所需要的时间,取决于机器可以存放的最大原料数,最大原料数越低,达到满效率所需的时间越短。
在搭建完模块框架产线后,我打开了我的教材,看见了这两个熟悉且折磨的老朋友:

我说怎么在设计的时候有种说不出来的的熟悉感,原来是你,Dijkstra
总所周知,贪心算法是以贪心著称:

“总是做出在当前来看最好的选择”这不就与对于每台机器,都以满效率作为设计目标是师出同门吗?甚至就连该算法的局限性都继承了下来
对于另一条产线,又有:

从一开始的通过公式计算的理论可行,再基于产物往上推进,到最后的产线搭建,这就是一个自底向上的设计过程。每一道中间产物的产线,都是多阶段决策问题中的一环,最后经由时间推进,以达到最佳决策——满效率。
总结:这并不是一篇结论性文章,因此也不会有结论性的总结,更多的是基于游戏特性引起的启发和思考,如若真是想证明些什么,那我或许想说:玩游戏其实也能激起并不亚于书籍和电影的思考。
以上