同一行和列裡不能有重複數字大家都知道,但是有些人對宮的概念不清楚,這就沒法玩了。請看下圖:

數字"2"上面的線是由兩條黑細線和灰色條組成的,數字"2"左面的線也是由兩條黑細線和灰色條組成的。
像這樣的線就是用來劃分宮的,被這樣的線劃分的每個區域就是一個宮,每一個宮裡面有四個、六個或是九個基本方格,對應四宮、六宮或是九宮。
上圖是四宮,所以每個區域(宮)有四個基本方格。
基本規則:
以九宮格為例,九宮格每一行有九個基本方格,每一列有九個基本方格,每一宮裡也有九個基本方格(我說的是完整的九宮格,普通難度的前幾關是不完整的)。當某一行的一個基本方格里出現了某個數字,例如數字"1",那麼這一行的其他八個基本方格里就不能再是"1",列與宮同理。
明白了上面那些就可以說基本方法了,以九宮格為例進行說明。為方便說明將九宮格的九個宮命名,如下:
左上宮 中上宮 右上宮
左中宮 中中宮 右中宮
左下宮 中下宮 右下宮

方法一:
接下來的方法暫命為方法一,便於區分其他方法。
這是專家難度第一關,在這一關裡已經給出了幾個數字"1",我們點擊其中一個數字"1",如下:

所有已經確定的數字"1"被系統標記為橘色(是橘色吧,對顏色更懂的如果認為不對可以糾正,前兩天玩"還有這種操作2"有一關分辨口紅顏色,讓我對分辨顏色不太自信了...),可以看到,圖中一共有五個數字"1"。
那麼,九宮格一共應該有幾個數字"1"呢?九宮格一共有九個"宮",每個"宮"裡都要有而且只能有一個數字"1"。所以,九宮格一共應該有九個"1"。
可以看到,上圖中還缺少四個"1"沒有被確定下來,我們先看看能不能把這還沒確定的"1"找出來。
先看中中宮,這個宮裡沒有數字"1"。並且,這個宮裡還剩四個空白的基本方格。那麼,哪個基本方格里是"1"呢?
請觀察中中宮周圍的宮裡的"1",根據中上宮裡的數字"1",我們知道這個"1"所在的這一列裡都不能再有"1"了。所以,在中中宮裡,數字"5"下面那兩個基本方格都不能是數字"1"。
所以,中中宮的數字"1"只能出現在這個宮裡數字"7"的下面。
再根據左中宮的數字"1",知道,那一行不能再有"1"。所以,中中宮裡數字"7"下面緊挨著數字"7"的方格里不是"1"。
那麼,中中宮的數字"1"就應該是在數字"7"下面隔著一個格的方格里,如下圖:

還剩三個"1"沒確定,但是,用這個方法找不到了。我們去找數字"2",如圖:

有五個數字"2",還剩四個沒確定。先確定左上宮裡的數字"2",根據中上宮、右上宮、左中宮這三個宮裡的數字"2",可以確定左上宮的數字"2",如下圖:

具體思路類比找數字"1"時的思路。接著,左下宮:

中下宮:

右下宮:

好了,所有的數字"2"都已經確定了。接下來,數字"3":

左下宮:

右下宮:
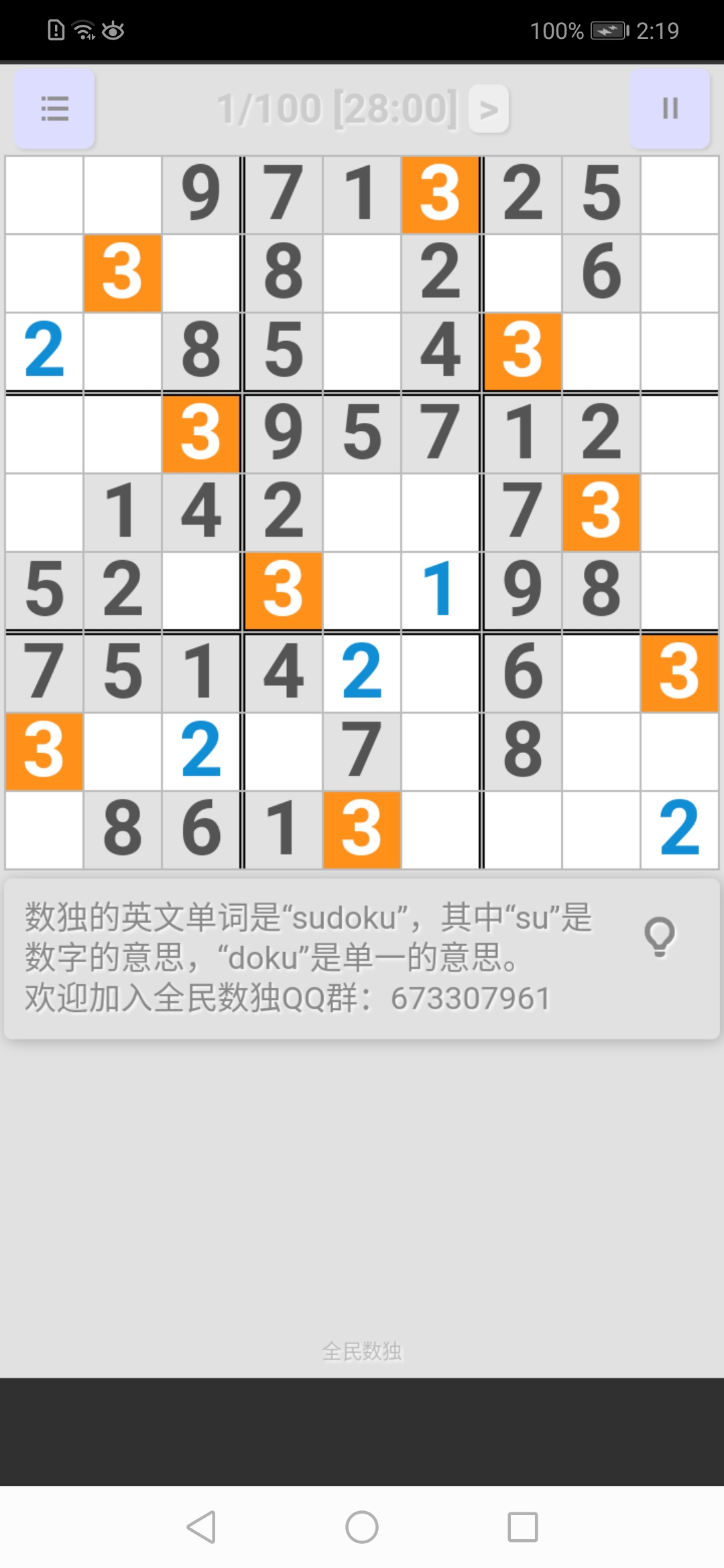
數字"4":
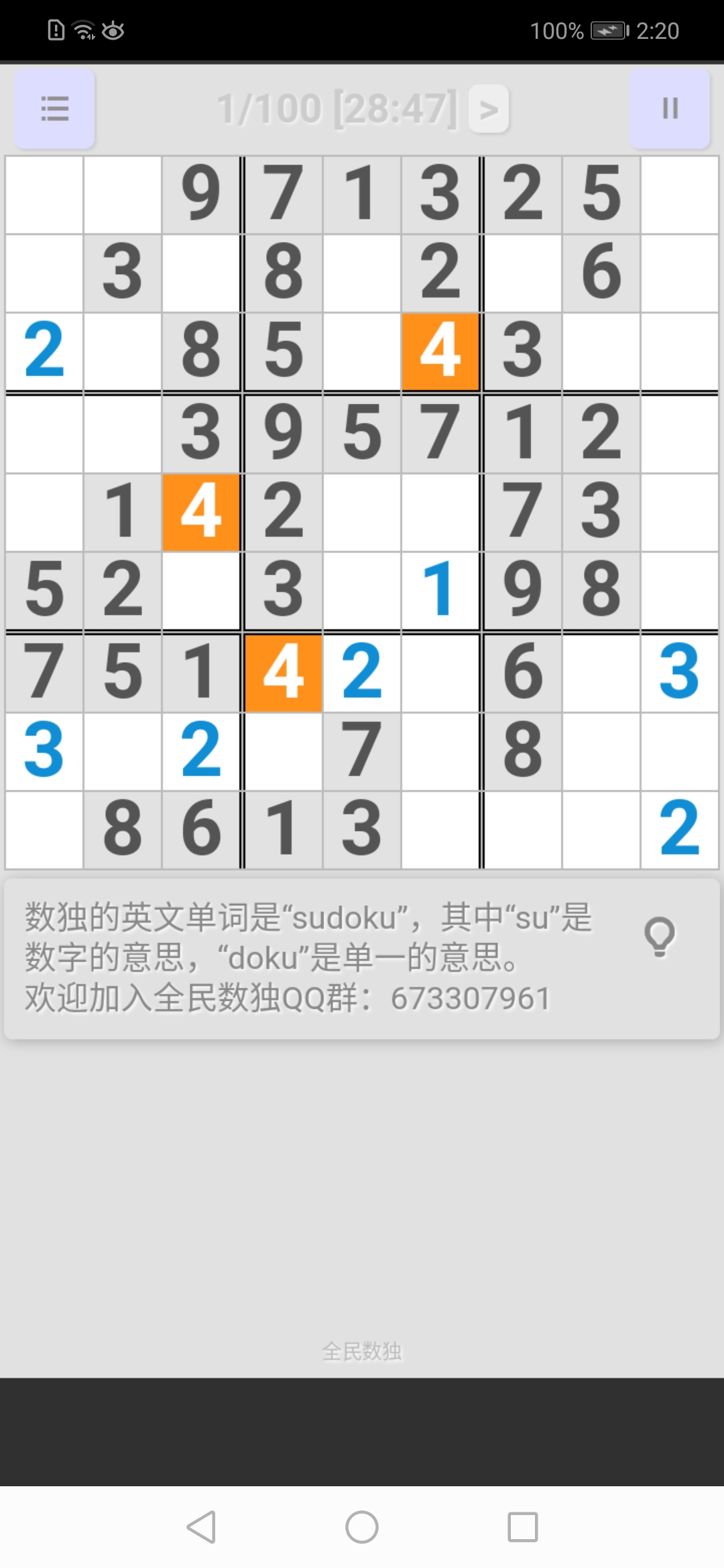
中中宮:
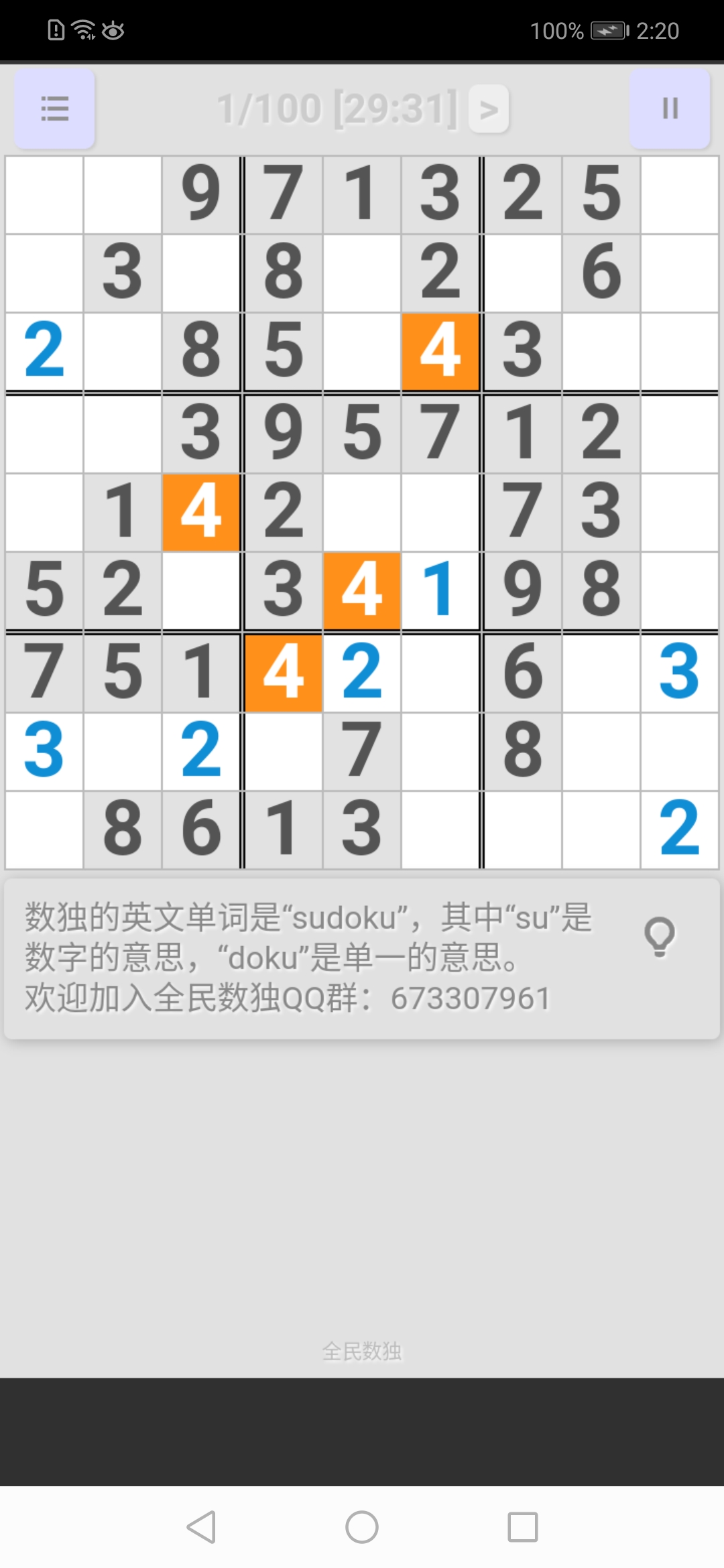
右中宮:
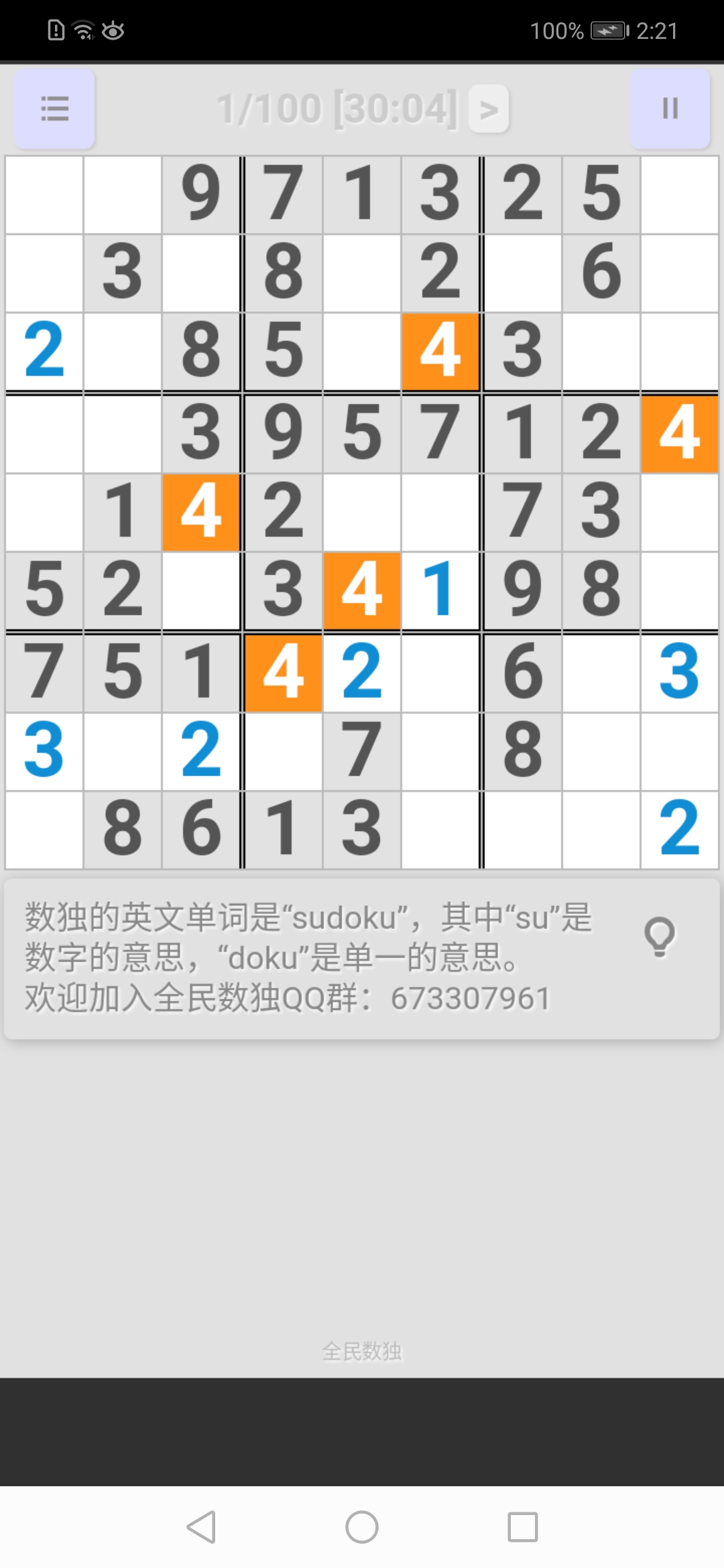
右上宮:
數字"5":
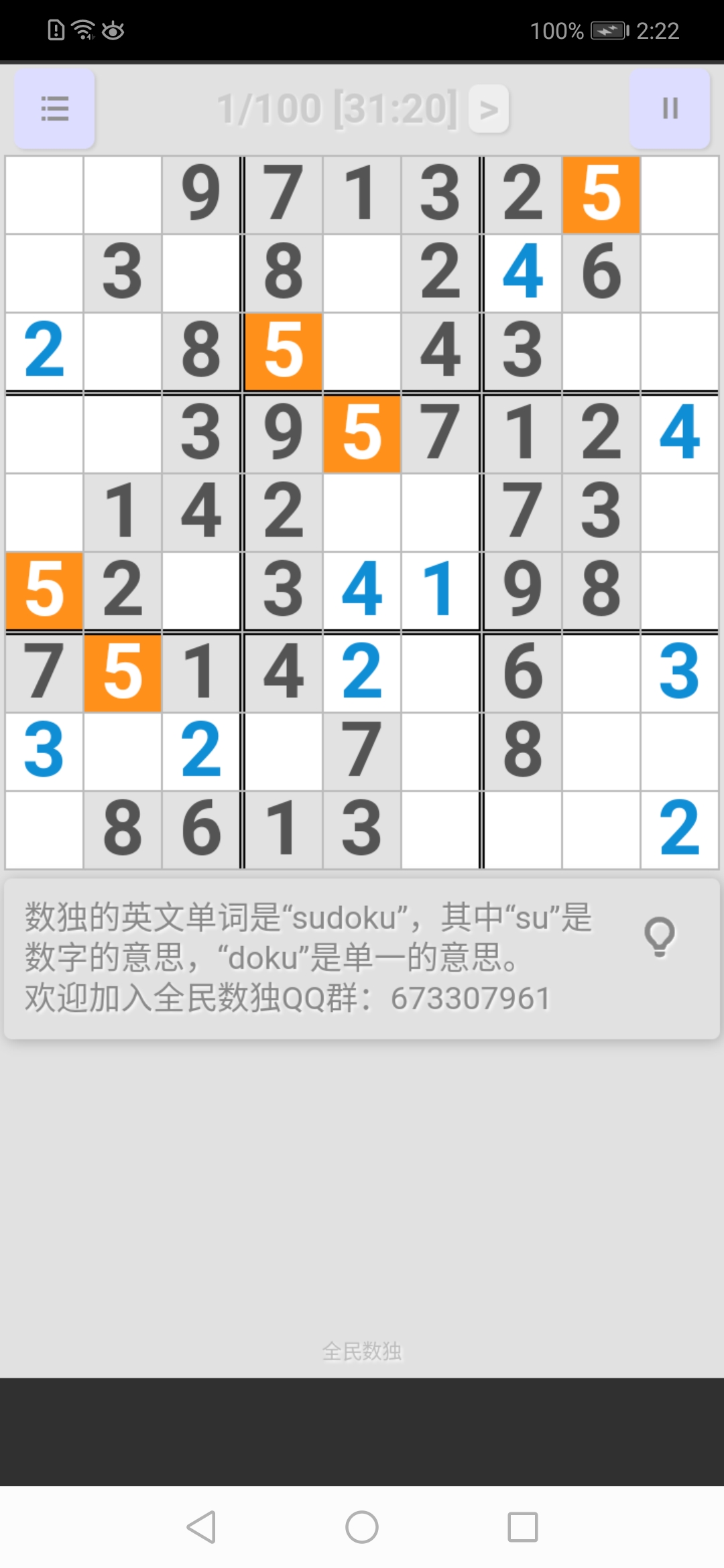
左上宮:
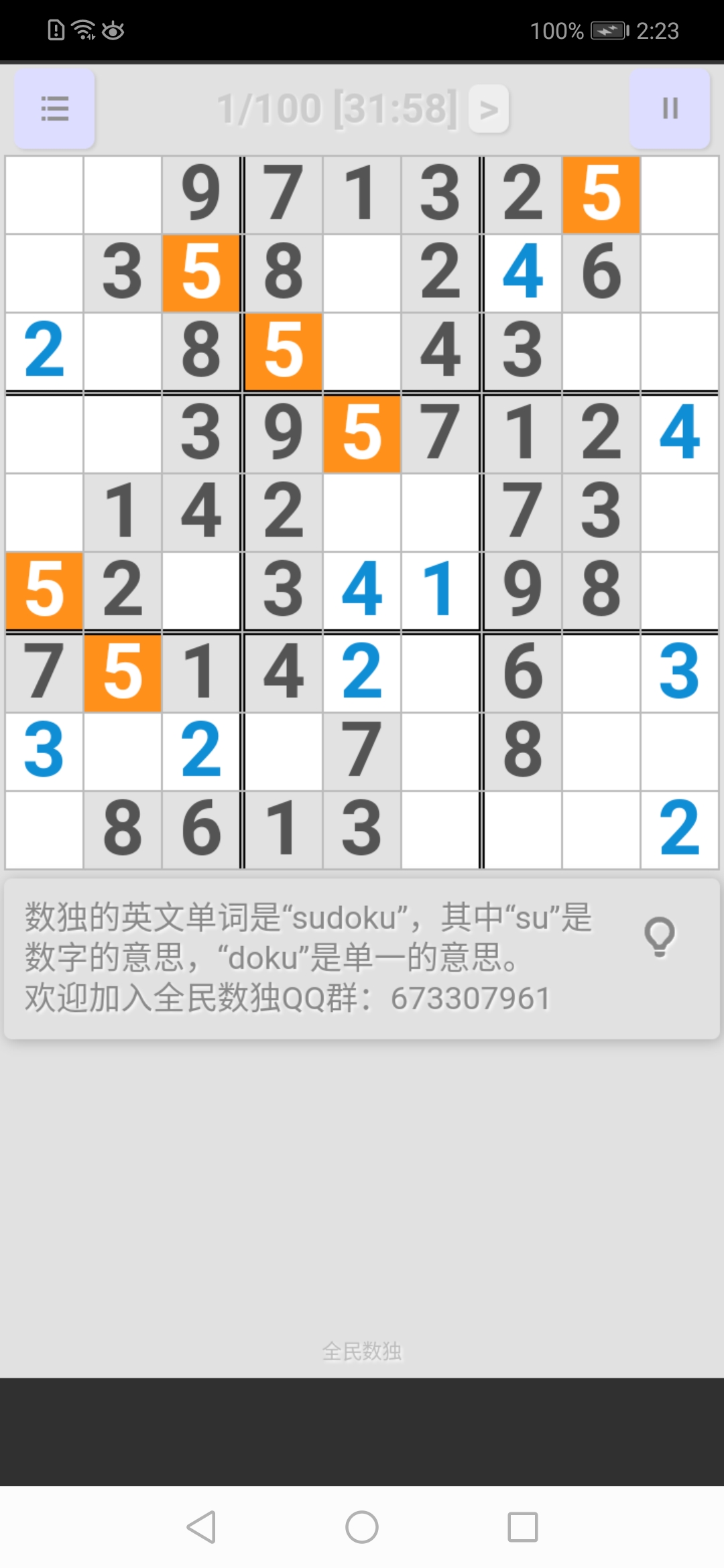
右中宮:
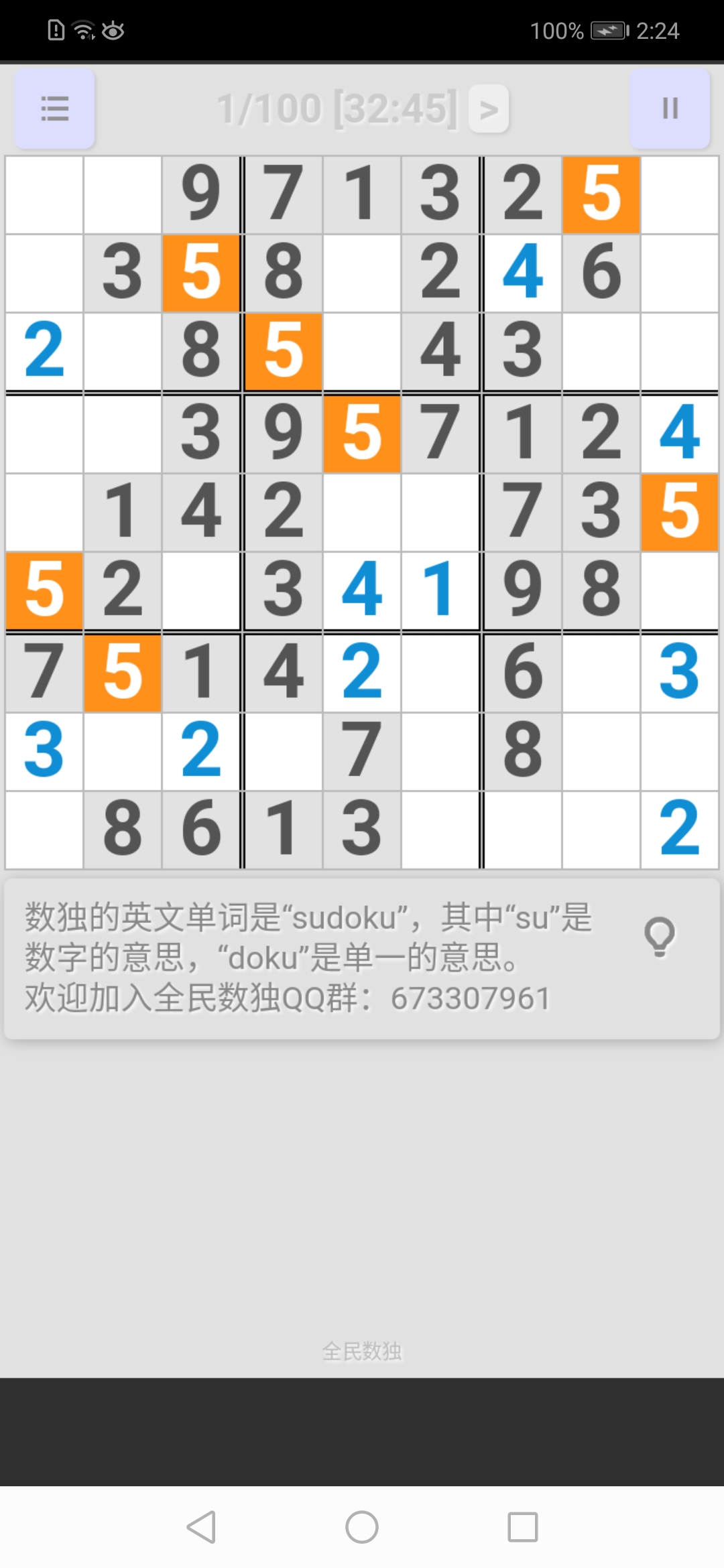
右下宮:
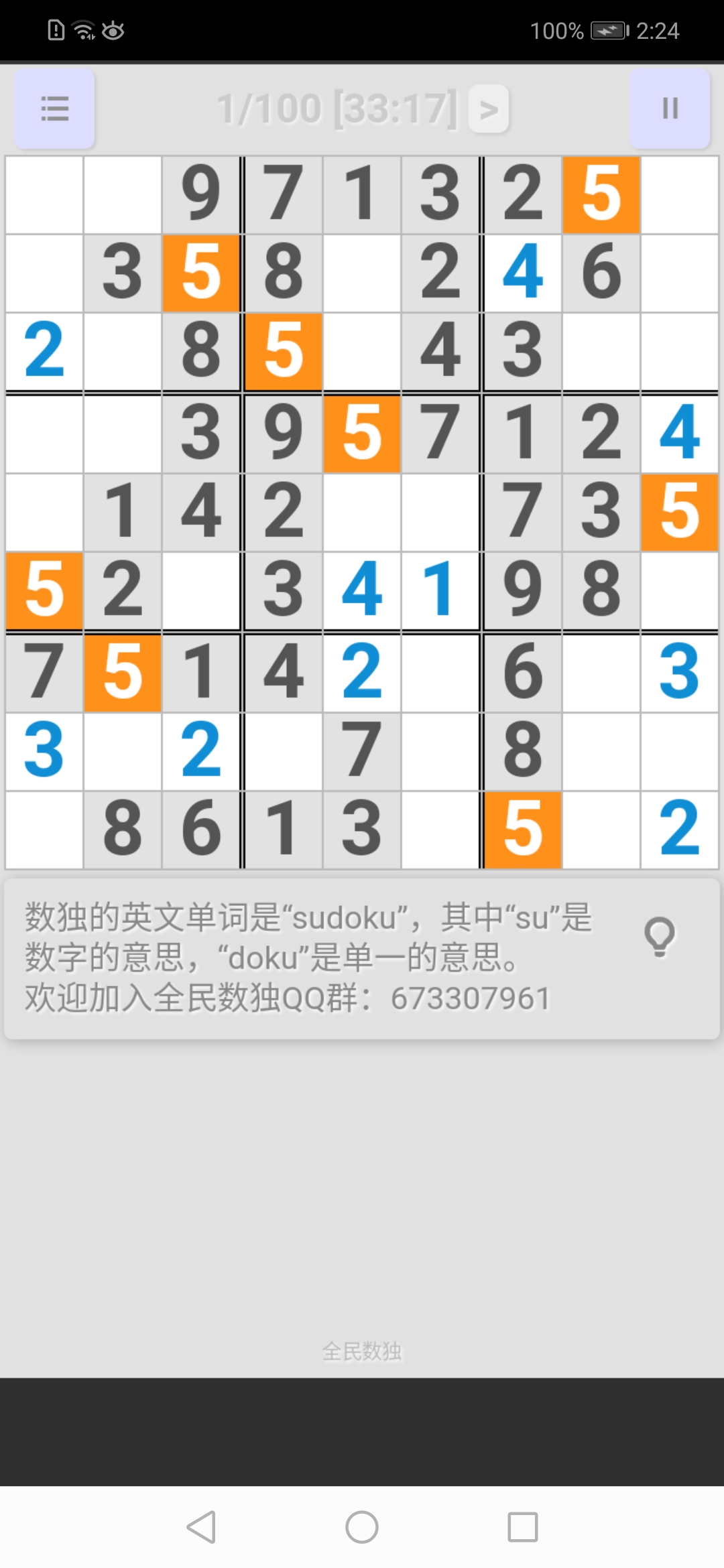
中下宮:
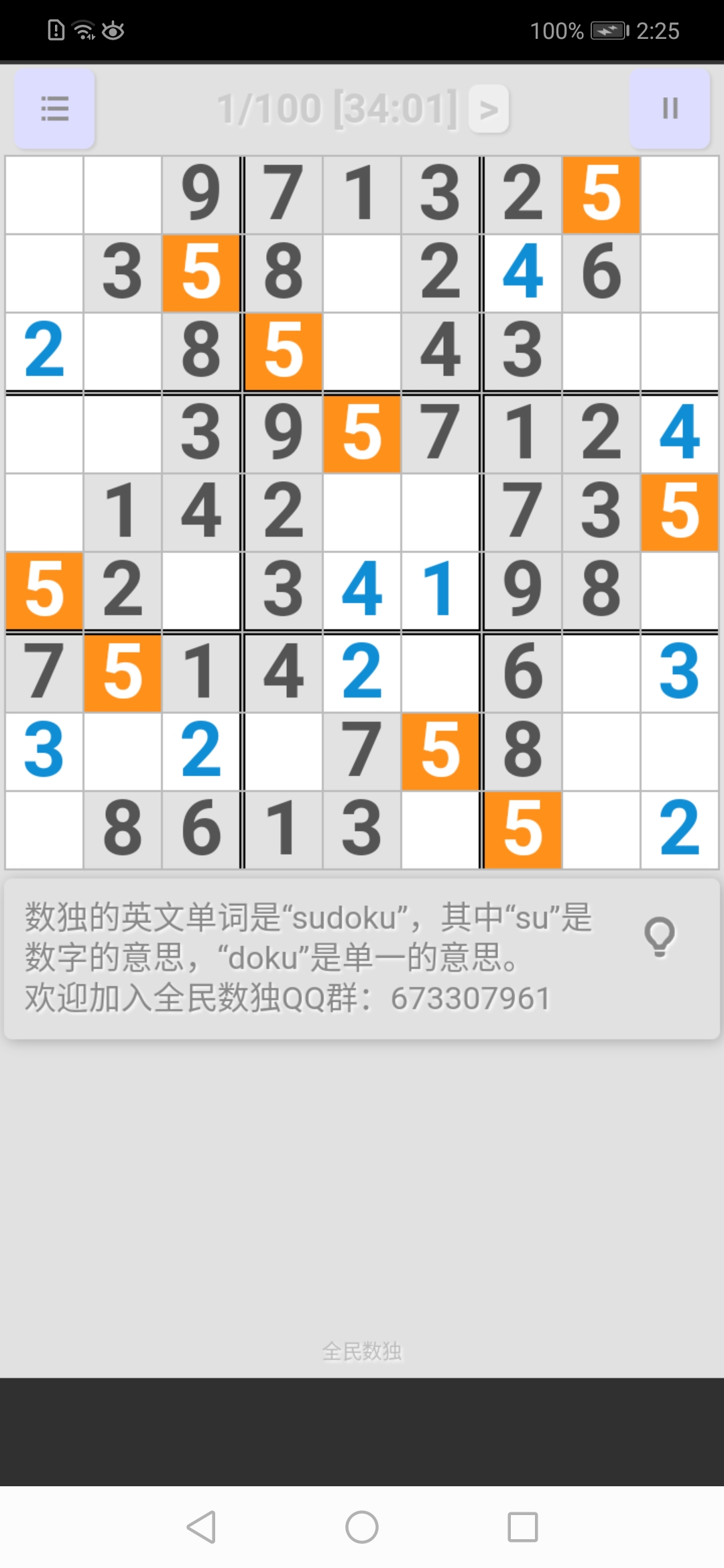
按照這個方法把所有數字過一遍直到"9",然後得到的圖是這樣的:
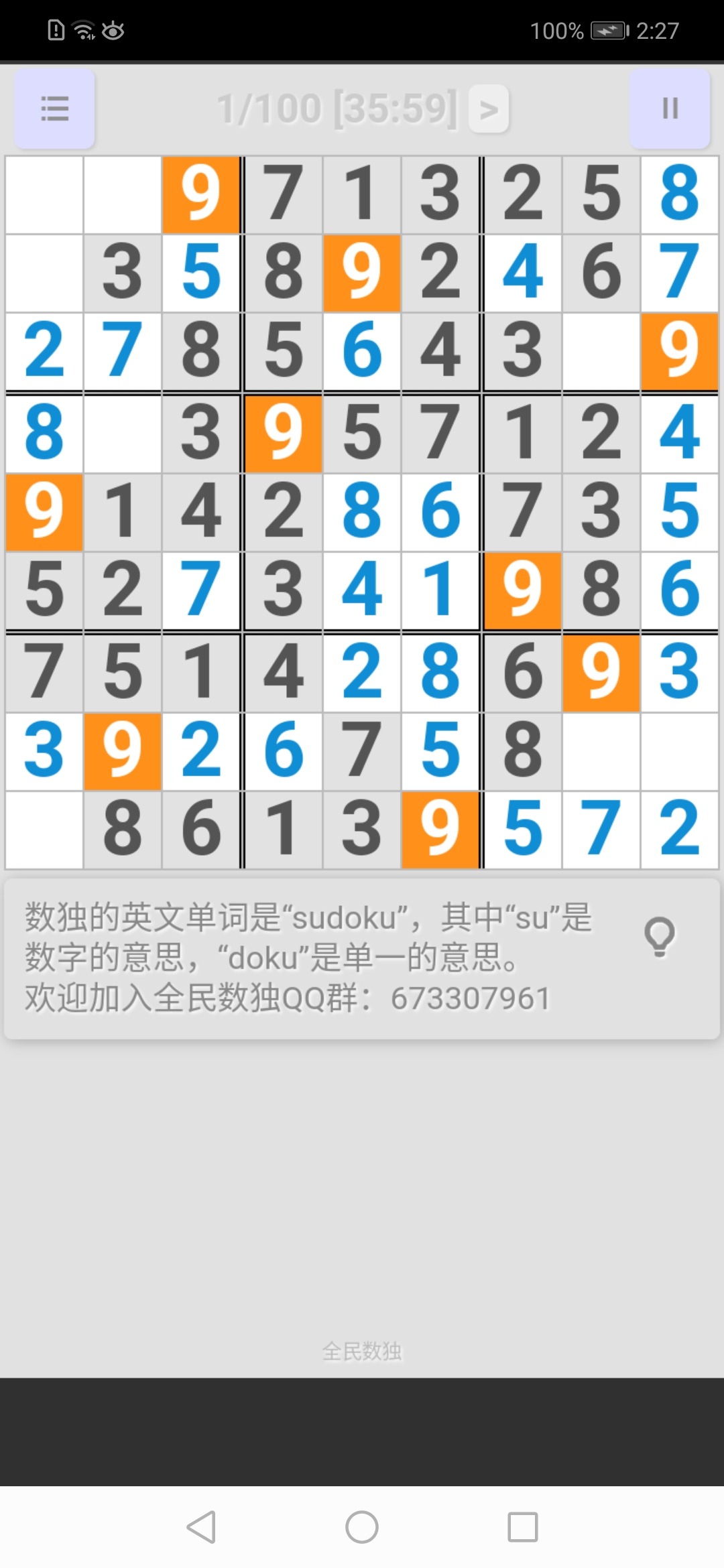
剩下那些空白的方格就很好確定了,我就不說了。
使用這個方法需要注意一點,因為我們是按照從"1"到"9"的順序找,但不一定能把前面的數字都找出來,這時,我們需要找後面的數字。當後面的數字確定了一些的時候,有可能會對前面的數字有幫助。就是說,當前面的數字進行不下去的時候找後面的數字,後面的數字確定了幾個之後再回去找前面的數字,也許之前無法確定的這時候卻可以確定下來。
因為,後面確定的數字是要佔格子的,這樣,空白的格子變少了,也就更容易找了。
所以,使用這個方法的正確方式是從"1"找到"9",找完一遍再從"1"找到"9",直到所有數字都找不到新的為止。這時,再考慮其他辦法。
依靠方法一並不能解出所有題目,下面說方法二。使用方法二的時候需要頻繁的在其中穿插使用方法一,所以,在看方法二之前請先詳細瞭解方法一。
方法二:
在講解之前先說兩件事,第一件事,命名行與列,命名如下:
第一行
第二行
第三行
.
.
.
第九行
第第第 第
一二三······九
列列列 列
第二件事,"標記"的使用,遊戲中有標記這個功能,在解題時需要用到,請先了解如何使用,不難。
進入正題,下圖是普通難度69關:

先使用方法一解,可以發現解到下圖的狀態就進行不下去了:

這時,我們從第一列開始逐列推算,根據左上宮剩餘空白方格的情況可知,還剩數字"1"和"6"沒確定,正好都在第一列。標記出來如圖:

這個標記的含義是(重點):第一列的數字"1"和數字"6"只能出現在被標記的這兩個方格里。(如果第一列的其他格里是"1"或"6",那左上宮的"1"和"6"怎麼辦?所以,只能出現在那兩個方格里)
好了,雖然這兩個方格哪個是"1"哪個是"6"還不知道,但至少確定範圍了。那麼,第一列裡還有哪些數字沒確定範圍呢?
數一數,"5"和"8"還不知道。最上面兩個方格已經被"1"和"6"佔了(它們兩個只能在這兩個方格里,又只有兩個方格,當然沒有其他數字的位置了),所以,"5"和"8"只能出現在最下面兩個方格里。標記出來,如圖:

同樣,這個標記的含義是:第一列的數字"5"和數字"8"只能出現在這兩個方格里。目前,還無法確定哪個是"5",哪個是"8"。沒關係,往下進行。
在推算第二列之前有個好消息,那就是:由於第一列"5"和"8"的這個位置,左下宮沒出現的數字"1"可以確定了。第一列最下面兩個方格已經沒有其他數字的位置了,所以"1"只能出現在下圖的位置:

是不是很有意思,之前用方法一無法確定的數字"1"就這麼被找出來了。
請記住(重點):在使用此方法(這裡指方法二)或是方法一的時候,一旦某一行、某一列、某一宮就差一個數字了,就馬上填充出來。
上面雖然"5"和"8"誰是誰還不知道,但範圍有了,左下宮就差"1"了。
下面推算第二列,第二列還差"3"和"5",標記出來,如圖:

推算第三列:
看圖可知第四行有個"1",所以第三列的"1"只能出現在下圖的位置:

看圖可知第六行有個"6",所以第三列的"6"只能出現在下圖的位置:

看圖可知第五行有個"8",所以第三列的"8"只能出現在下圖的位置:

推算第四列:
看圖可知第四、七行分別有個"1",這樣第四列的"1"就有三個可能的位置,分別位於第四列的二、六、八行。像這樣可能位置多於兩個的我們不標記,位置多了繁瑣,容易出錯,而且意義不大。
找"2",看圖可知第二、四、六、七行分別有個"2",所以第四列的"2"只能出現在第八行的位置:

這樣,第八行被"2"佔了。那麼,"1"就只剩兩個可能的位置了。這時,我們就標記出來,如圖:

標記"5":

標記"6":

標記"9":

這時,我們發現第四列的第七行只有一個"6"。也就是說,只有"6"可能出現在這個位置,那這個位置就是"6",填充出來:

這樣,第二行的標記"6"就沒意義了,刪掉:

並且,由於第四列這個"6"的確定,我們發現整個第七行只差數字"8"了,填充出來:

然後,右下宮又只差數字"6"了,填充出來:

推算第五列,我們發現只有"7"有兩個可能的位置,其他數字可能出現的位置都多於兩個。標記出來:

推算第六列:

推算第七列:

推算第八列:

推算第九列,標記"3":

由於第五行有個"8",所以,第九列的"8"確定了:

"3"隨之確定:

至此,我們把第一到九列都過了一遍。
重點:此時,使用方法一。
"1"、"2"仍然找不到。
找"3",如上圖,所有的"3"被系統顯示為橘色,左中宮的"3"能夠確定出來,如圖:

第二列就差"5":

用方法一找中中宮的"3":

中上宮的"3":

右上宮的"3":

一直到"9"發現仍然找不出來,進行不下去,如圖:






沒關係,再回來使用方法二。
第六列由於剛才確定了幾個數字,"1"的範圍縮小了,標記出來:

"9"也可以標記了:

第七列的"5"可以標記了:

標記"7":

第七列還有"6"沒有標記,但是我們發現,第六行有個"6"。說明第七列的第六行不是"6",那就只能是"5"了,填充:

這樣,第四行的標記"5"就要刪掉:

第八列,"7"標記出來:

然後,請點擊"5":

發現第四列的"5"不能出現在第六行,那就只能在第四行:

第六行的標記"5"刪掉:

發現第六行只能是"1",填充:

第二行就是"9":

由於第六行出現了"1",所以,第三列的"1"在第五行:

刪掉第三列第六行的標記"1":

第六行只能是"8":

"6":

使用方法一,右中宮的"6"可以確定了:

這樣,第七列的"4"只能出現在第四行:

第七列的"7":

右中宮的"7":

使用方法一,中上宮的"7":

刪掉第五列的標記"7":

刪掉第八列的標記"7":

第二行有"9",所以第八列的"9":

第八列的"6":

第二行出現"6",所以,第一列只能"1"在第二行:

第一列的"6":

使用方法一,中上宮的"1":

中下宮的"1":

使用方法一,中上宮的"6":

中上宮的"2":

第六列的"9":

刪掉第六列的標記"1"和標記"2":

使用方法一,中中宮的"8":

中下宮的"8":

第九行出現"8",第一列的"8":

第一列的"5":

至此,就差不多了,剩餘幾個空很簡單。