量子糾纏(quantum entanglement),又譯量子纏結,是一種量子力學現象,其定義上描述複合系統(具有兩個以上的成員系統)之一類特殊的量子態,此量子態無法分解為成員系統各自量子態之張量積(tensor product)。
量子糾纏的定義;人們說的量子糾纏,是指一個紅粒子和一個藍粒子,在沒有時間的第三空間裡發生了神秘的關聯,稱為量子糾纏。
一個紅粒子狀態=0,像硬幣的反面,那麼反面是紅=0;
一個蘭粒子狀態=1,像硬幣的正面,那麼正面是蘭=1;
我們看博弈聖經這樣描述它們的關係;在我們眼前的每一飛秒,都有一個紅蘭的紅粒子通過,接著一個蘭粒子通過,一替一連續性地變換,這就是大自然的一個均衡模式,任何人猜測0101010101或者是紅蘭紅蘭紅蘭這個隨機系統中的某一個粒子,都不會大於一半,這時熵升高,越猜越亂,這就是人在博弈中的熵證據。摘自《人類未知的藍色檔案》一文
量子糾纏是粒子在由兩個或兩個以上粒子組成系統中相互影響影響的現象,雖然粒子在空間上可能分開。
在物理學中,量子糾纏是指存在這樣一些態:A,B,C,…,在時,這些態之間不存在任何相互作用。當時,它們的狀態由Hibert空間HA,HB,HC...,中的矢量所描述,由A,B,C空間構成的量子系統ABC則由Hibert空間中矢量所描述,則這樣的態被稱為比Hibert空間的直積態,否則稱態是糾纏態,也就是說,如果存在糾纏態,就至少要有兩個以上的量子態進行疊加。
量子糾纏說明在兩個或兩個以上的穩定粒子間,會有強的量子關聯。例如在雙光子糾纏態中,向左(或向右)運動的光子既非左旋,也非右旋,既無所謂的x偏振,也無所謂的y偏振,實際上無論自旋或其投影,在測量之前並不存在。在未測之時,二粒子態本來是不可分割的。
【現象解釋】
量子糾纏所代表的在量子世界中的普遍量子關聯則成為組成世界的基本的關聯關係。或許用糾纏的觀點來解釋“夸克禁閉”之謎。當一個質子處於基態附近的狀態時,它的各種性質可以相當滿意地用三個價夸克的結構來說明。但是實驗上至今不能分離出電荷為的u夸克或()的d夸克,這是由於夸克之間存在著極強的量子關聯,後者是如此之強,以至於夸克不能再作為普通意義下的結構性粒子。通常所說的結構粒子a和b組成一個複合粒子c時的結合能遠小於a和b的靜能之和,a或b的自由態與束縛態的差別是不大的。而核子內的夸克在“取出”的過程中大變而特變,人們看到的只能是整數電荷的,介子等強子。同一個質子,在不同的過程中有不同的表現,在理解它時需要考慮不同的組分和不同的動力學。一個質子在本質上是一個無限的客體。實質上整個宇宙是一個整體的能量慣性體系包括實在的粒子和空間,由於能量慣性的存在,整個能量體系時刻按一定的能量運動規律運動,宇宙中的每一個粒子作為宇宙能量的一分子它本身的能量慣性狀態始終與宇宙環境保持一致即能量的穩定性,它們的電磁能量波始終存在著相互作用。當倆物質粒子同時處於某一狀態即儘量使之處於基態或能量控制編碼態,它們在相互作用時產生了電磁能量慣性互動及量子糾纏現象。因此,物質具有能量然而人們只能從物質的相互作用中獲得並得到利用。
【公式表達】
1935年,愛因斯坦、波多爾斯基和羅森(Einstein Podolsky and Rosen)等人提出一種波,其量子態:
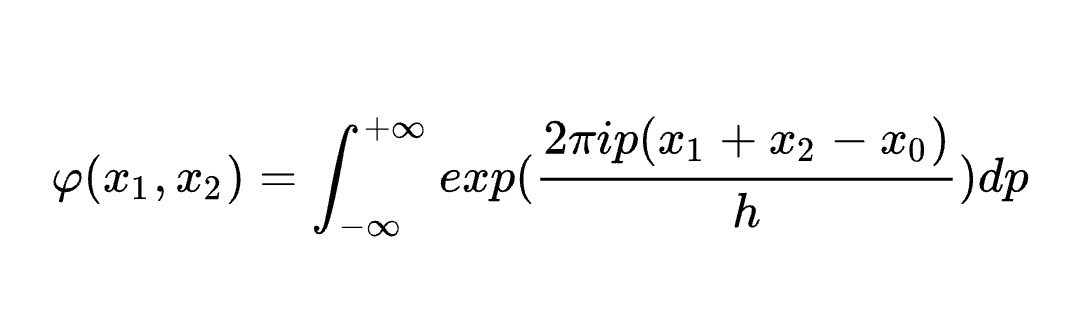
其中分別代表了兩個粒子的座標,這樣一個量子態的基本特徵是在任何表象下,它都不可以寫成兩個子系統的量子態的直積的形式:
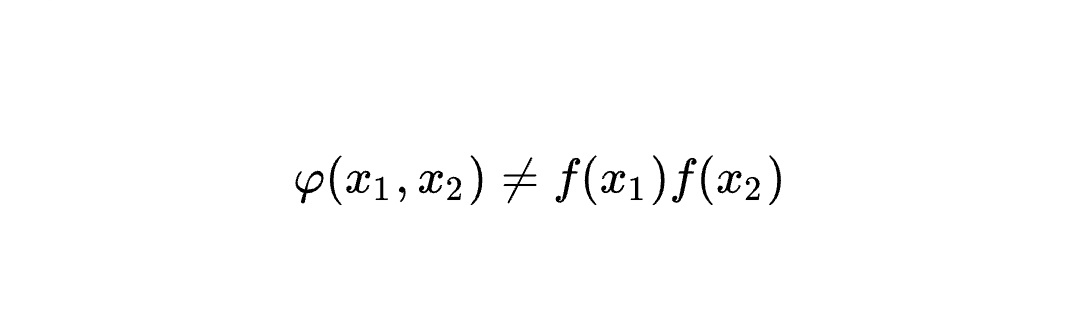
這樣的量子態稱為糾纏態。
【量子描述】
所謂的糾纏度是指所研究的糾纏態攜帶糾纏的量的多少。對糾纏度的描述,實質上是對不同糾纏態之間建立定量的可比關係。糾纏狀態所糾纏的粒子數量越多,對經典物理學的偏離越明顯,獲得有用量子效應的機會就越大。所以,在量子信息領域中,糾纏通常被看作是非局域的“信息源”。
於是,如何對糾纏定量化就顯得十分重要。但對於兩體純態而言,它仍是兩體純態唯一合理的糾纏度定義。對於多體糾纏度的描述的研究到目前為止仍沒有得到真正的解決,人們仍未放棄尋找一種物理意義上更為鮮明、簡單、易於求解的糾纏度的描述。
【量子特點】
量子糾纏並非信息傳遞,事實上信息不可能從一個粒子傳到另一個粒子。即使用光速將它們分開,信息也不可能在測量時從一個地方傳到另一個地方。
量子力學是非定域的理論,這一點已被違背貝爾不等式的實驗結果所證實,因此,量子力學展現出許多反直觀的效應。量子力學中不能表示成直積形式的態稱為糾纏態。糾纏態之間的關聯不能被經典地解釋。所謂量子糾纏指的是兩個或多個量子系統之間存在非定域、非經典的強關聯。量子糾纏涉及實在性、定域性、隱變量以及測量理論等量子力學的基本問題,並在量子計算和量子通信的研究中起著重要的作用。
多體系的量子態的最普遍形式是糾纏態,而能表示成直積形式的非糾纏態只是一種很特殊的量子態。歷史上,糾纏態的概念最早出現在1935年薛定諤關於“貓態”的論文中。糾纏態對於瞭解量子力學的基本概念具有重要意義,已在一些前沿領域中得到應用,特別是在量子信息方面(例如,量子遠程通信)。我國科學家潘建偉已經成功的製備了8粒子最大糾纏態。