落日間鏈接: Stephen Wolfram 作為多重計算系統的遊戲和謎題 (2022)
譯按
我們知道,複雜系統最重要的特徵就是具有湧現行為,簡單規則的運用誕生出複雜而難以預測的行為——也就是說,在系統的規則和行為之間存在一種認知鴻溝(Epistemic gap)。
這種認知鴻溝能有多大?鴻溝對面的那個世界究竟有多複雜?我們能夠在這些問題上作出某種程度上的比較,甚至量化的計算嗎?
除了一種單純的好奇心在促使我們作出這樣的發問,這個問題還有更加現實的意義。複雜系統有很多實際應用。在遊戲設計中,遊戲規則的湧現行為使得一個遊戲具有深度和趣味性;在計算創意學中,創作機制的湧現行為決定了我們在多大程度上可以將這個系統看作是具有想象力的。我們有辦法去比較兩個遊戲誰更有深度,或者兩個自動創作系統誰更具想象力嗎?
Wolfram的這篇文章,提出了一種可視化和具體探討湧現行為的豐富程度的思路——也就是多重計算過程(Multicomputational Process)的概念。作者以幾個傳統的遊戲或者說謎題為例,在計算機的強大算力下得以用圖(Graph)的方式去可視化這些遊戲規則下的可能遊玩路線。能夠將遊戲規則的深度與這些圖的許多直觀特徵掛鉤,也得以將一些圖論中早已建立的理論遷移到對遊戲趣味性的討論語境下。我們能在這些圖上直接「看到」一個遊戲有多有趣、有多難、對哪個玩家更有利——更重要的是,這個遊戲規則所構建的系統有多複雜。
在我們已經感受到許多看似簡單的遊戲竟有著如此令人歎為觀止的複雜性之後,作者又引出 Rulial space(所有可能的規則以及這些規則的所有應用方式所組成的空間)的概念,讓我們去想象可計算的宇宙這個複雜系統,其複雜程度又形成了怎樣的一種維度碾壓。這足以讓一個並沒有在仰望星空的人,也在「宇宙的浩瀚」之下啞口失言。
我作為一個AI研究者,雖然很早就接觸到諸如基於蒙特卡洛樹搜索和加強學習的遊戲AI,以及神經網絡或遺傳算法生成遊戲規則之類的計算機技術,但這篇文章讓我第一次感嘆,我們做的是一些多麼大膽的「試圖與宇宙通靈」的事情。
厭氧菌
校按
我是在嘗試使用 Wolfram 語言和理解其創始人龐大,且業已進入工業化和商業可持續道路的願景中發現了這篇文章的,我立刻意識到這是非常有趣的和稀有的研究嘗試,就如同複雜科學的出現,開始將目光從過大的天體、過小的原子而轉向日常生活中如水龍頭的水滴,湍流,氣體,海岸線這樣的難以計算的事物;或許就如痴迷於國際象棋的克勞德·香農一樣,我們是不是也可以用科學的視角來嚴肅且深入地研究一些「很簡單」的遊戲,就像這篇文章一樣?
這不是一件容易的事,就像 Wolfram 試圖進行的,實際上是通過人類層面對遊戲的思考來類比對照量子力學一樣,在這篇文章的例子中,即便有強大,能將大量計算可視化的 Wolfram 語言和框架的幫助,遊戲的簡單規則中蘊含著的人類語言和思維難以捕捉的可能性,以及「多重計算的不可還原性」也遠遠足以讓人意識到遊戲中存在的某些驚人的事物。
遊戲設計者到底創造出來的是什麼?
存在於時間中的我們「只能」在一次次的重複中穿過這些複雜分支的多路圖,用直覺,靈感,積累去捕捉,去做出某些棋子的決定,那四維生物是否能夠一瞬間同時看到所有魔方轉動的可能性呢?當我們哀嘆人類棋手敗於AI,但我卻覺得,人類作為如此不擅長計算的生物(所謂計算受限的實體 computationally bounded entities),居然能夠在這樣離散和計算化的博弈中抗衡深度神經網絡多少億萬次,和多少參數的計算,這以足以令人驚奇了。
那麼,當物理學家和數學家取道於遊戲來闡述些什麼事時,我們或許應該問:為何遊戲總是被取道,遊戲為何有能力,去成為這些最深奧知識的中介呢?遊戲和它們,和世界的規則,秘密之間是什麼關係?在這個意義上,就像是數學是對世界的抽象,而揭示出某些面向,而遊戲也總是某種「揭示」,展露出了某種現實,並且成為正在發生的現實。
很多對於計算機的哲學討論有著離散和連續/模擬和數字的對照,但在物理學的視角下,下降到足夠低的層級(甚至是普朗克時間),就像Wolfram在文章開頭所說的「物理世界在最低層次上是離散的——就像遊戲和謎題一樣」,而對於遊戲來說,自然最終是離散亦或是連續的並非重點,重要的是遊戲製作者如何有能力在不同的層面構建離散和聯繫的關聯,並且以人類視角(Humanizing),將這些語言難以捕捉,計算不可還原的多路過程展開。
這篇文章所展示的計算分析方法,以及對現有遊戲的計算性解構,或許也能直接地給遊戲設計的思考帶來的啟發,「當我們發現多路圖在某種程度上「難以解碼(decode)」時,我們就會得到一個豐富的、吸引人的遊戲或謎題」,而也正是一種對於遊戲設計所在著手處理的事物的一次正面且直接的計算呈現,遊戲設計在做什麼?在某種意義上來說,便正是在調校,試驗這些不可還原的多路和分支圖的形態。
本文得益於 Wolfram 語言的強大計算能力,而卻也只能從極簡的例子出發,更無涉電子遊戲,動作遊戲等,不禁令人好奇,如 MOBA 遊戲是否能以這種方式分析?人工智能視角下的這些多路圖的空間是怎樣的?遊戲是什麼東西「理想模型」?種種這也問題依舊引起我們的好奇,而從此文其中得以一窺的錯綜複雜,大概也正是遊戲之難以言說的緣故吧。
* 非常開心能夠與厭氧菌再再次合作,本篇超長文章的翻譯要仰仗於她的耐心與細緻與學識,歡迎更多人關注她關於計算機創意學,賽博文本,湧現敘事的寶藏菌群反應器
葉梓濤
落日間
Stephen Wolfram

斯蒂芬·沃爾夫拉姆(Stephen Wolfram)是 Mathematica,Wolfram | Alpha 和 Wolfram 語言的創始人,《一種新科學》(A New Kind of Science)的作者,Wolfram 物理計劃的發起人,以及Wolfram Research 公司的創始人和首席執行官。在四十多年的時間裡,他一直是計算思維發展和應用的先驅ーー並在科學、技術和商業領域做出許多發現、發明和創新。
沃爾夫拉姆1959年出生於倫敦,曾就讀於伊頓公學、牛津大學和加州理工學院。他在15歲時發表了第一篇科學論文,並在20歲時獲得了加州理工學院的理論物理學博士學位。沃爾夫拉姆早期的科學工作主要是在高能物理學、量子場論和宇宙學方面,其中包括一些現在已經成為經典的結果。他從1973年開始使用計算機,迅速成為新興科學計算領域的領導者。1979年,他開始構建smp - 第一個現代計算機代數系統,並於1981年商業化發佈。
為了表彰他在物理學和計算機方面的早期工作,沃爾夫拉姆在1981年成為麥克阿瑟獎學金(MacArthur Fellowship)最年輕的獲得者。1981年底,他開始了一個雄心勃勃的科學新方向,旨在理解自然界複雜性的起源。他第一個關鍵想法是使用計算機實驗來研究被稱為元胞自動機(cellular automata)的簡單計算機程序的行為。這讓他對複雜性的起源有了一系列驚人的發現。沃爾夫拉姆發表的論文迅速產生了重大影響,為他稱為複雜系統研究的新興領域奠定了基礎。
20世紀80年代中期,沃爾夫拉姆繼續他在複雜性方面的工作,發現了計算和自然之間的一些基本聯繫,並創造了諸如計算不可還原性(本篇中提及)等概念。沃爾夫拉姆的工作帶來了廣泛的應用,併為複雜性理論和人工生命等計劃提供了主要的科學基礎。沃爾夫拉姆本人用他的想法開發了一種新的隨機生成系統和一種計算流體動力學的新方法——這兩種方法現在都被廣泛使用。
隨著他在複雜系統研究方面的科學工作,沃爾夫拉姆於1986年創辦了該領域的第一本雜誌《複雜系統》(Complex Systems),並建立了其第一個研究中心。在經歷了一段非常成功的學術生涯後——先是在加州理工學院,然後在普林斯頓高級研究院,最後在伊利諾斯州大學擔任物理、數學和計算機科學教授——沃爾夫拉姆創立了 Wolfram Research, Inc.。
沃爾夫拉姆在1986年底開始開發Mathematica。Mathematica的第一個版本於1988年6月23日發佈,立即被譽為計算領域的重大進步。在隨後的幾年裡,Mathematica的受歡迎程度迅速增長,Wolfram Research 成為軟件行業的世界領導者,在技術和商業方面的卓越被廣泛認可。從它最初作為一個技術計算系統開始,Mathematica在過去的幾年裡在範圍上急劇增長——在超過30年的過程中,它在許多領域和行業中負責許多重要的發明和發現,以及成為一代又一代學生教育的中心工具。
1991年,沃爾夫拉姆開始把他的時間分配在Mathematica開發和科學研究之間。在20世紀80年代中期工作的基礎上,現在又有了Mathematica作為工具,迅速取得了一系列重大的新發現。到了20世紀90年代中期,他的發現使他發展出了一個全新的概念框架,然後在90年代剩下的時間裡,他不僅將這個框架應用於新的問題,而且還應用於物理學、生物學、計算機科學、數學和其他幾個領域中許多現存的基礎問題。
經過十多年高度集中的工作,沃爾夫拉姆終於在他1200頁的《一種新科學》一書中描述了他的成就。這本書於2002年5月14日發行,廣受好評,並立即成為暢銷書。它的出版被視為開啟了科學領域具有歷史重要性的範式轉變,每年都有新的含義出現。《一種新科學》包含或激發了許多具體的發現,包括最簡單的邏輯公理系統和最簡單的通用圖靈機。
基於Mathematica和《一種新科學》的思想,沃爾夫拉姆開始了一個更雄心勃勃的項目:構建一個系統,使世界上儘可能多的知識可以立即計算,並讓每個人都可以訪問。Wolfram | Alpha在2009年5月的發佈被廣泛認為是歷史性的一步,它為計算和人工智能定義了一個新的維度——現在數百萬人每天都依賴它直接或通過智能助手(如Siri和Alexa)計算答案。
2014年,沃爾夫拉姆取得了另一個突破,在 Mathematica 和 Wolfram|Alpha 的基礎上創建了Wolfram 語言。基於沃爾夫拉姆在過去三十年中開發的前所未有的深度技術棧,Wolfram語言引入了全尺度計算語言(full-scale computational language)的新概念,它集成了大量關於計算和世界的知識,從而實現計算性描述和自動化的新水平,這可以作為大量基於計算的新領域的基礎。
2020年,在近30年發展的思想基礎上,沃爾夫拉姆宣佈在發現物理學基本理論方面取得突破,並啟動了Wolfram物理學計劃,以鼓勵廣泛參與這一雄心勃勃的歷史性項目。
stephenwolfram主頁
「然後當他開始研究遊戲……」
原文鏈接:點擊跳轉
譯者:厭氧菌
校對:葉梓濤
本文翻譯已經獲得授權
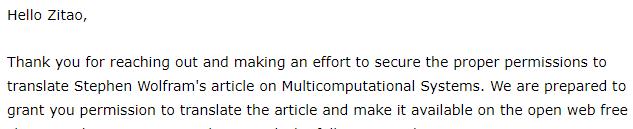
校注:此外,本文的原文鏈接中的每一張圖都是用 Wolfram 語言進行編程並可以直接複製出源碼,你可以在 Wolfram Mathematica 或者是 Wolfram Cloud 這樣的編輯器中展開,並且進行計算和生成驗證的,甚至進行交互,如下:

Games and Puzzles as Multicomputational Systems
June 8, 2022
日常視角下的多重計算過程
Humanizing Multicomputational Processes
多重計算(Multicomputational)是「Wolfram 物理項目」( Wolfram Physics Project)的核心概念之一,尤其是我們對量子力學的新興理解的核心。但是,如何才能對從一開始就很抽象的多重計算的概念有一個直觀的認識呢?
我相信,一個好的方法是在熟悉的系統和情況中看到它起作用。
我在這裡探討一個似乎特別好的例子:遊戲和謎題。
人們可能不會想到,像眾所周知的遊戲和謎題這樣的日常事物會與量子力學這樣的形式化理論有任何聯繫。但是多重計算的觀點提供了一個關聯。事實上,我們可以把存在「有趣的」遊戲和謎題的這種恰好的可能性本身,與多重計算的一個核心現象聯繫起來,即多重計算的不可還原性(multicomputational irreducibility)。
譯註:「多重計算的不可還原性」這個翻譯中的「還原」含義類似與「還原論」中的「還原」,有將複雜的事物歸結到簡單事物的含義
在一個普通的計算系統中,系統的每個狀態都有一個唯一的後續狀態(successor),而且最終有一個單一的時間線來定義一個計算過程。但在多重計算系統中,關鍵就在於每個狀態可以有多個後續狀態——追蹤它們的行為定義了一個由時間線程的分支和合並組成的一個完整的多路圖(multiway graph)。而關鍵就在於,這與人們如何思考典型的遊戲和謎題直接相關。
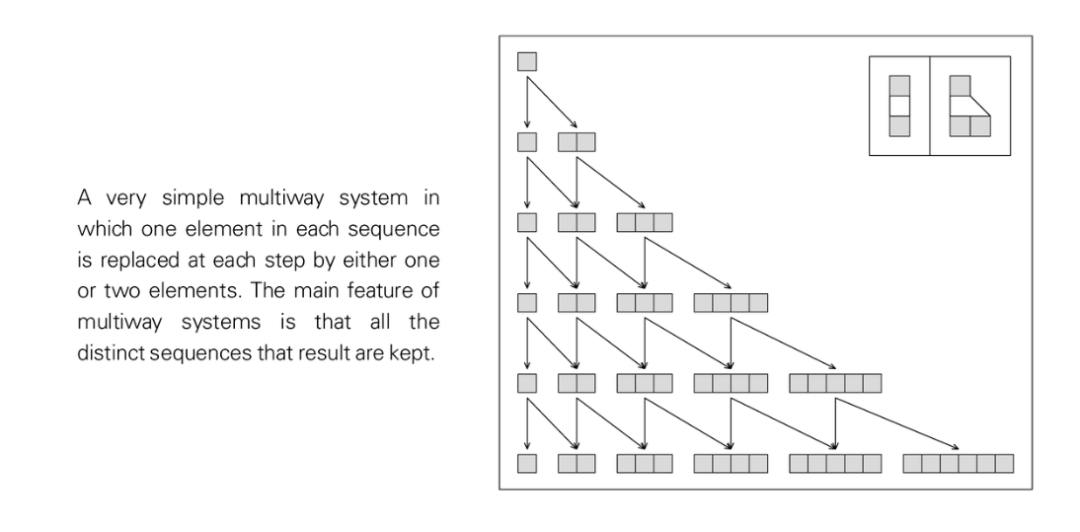
給定某個遊戲或謎題的一個特定狀態,玩家通常必須決定下一步該做什麼。他們通常有很多選擇可以做,這個時候多重計算的概念就出現了。在一次特定的遊戲過程(實例 instance)中,他們會做出一個特定的選擇。而多重計算範式(paradigm)的關鍵,是全局地看待所有可能選擇的結果——併產生一個代表這些選擇的多路圖(Multiway Graph)。
為遊戲和謎題構造這樣的多路圖的做法實際上已經存在了100多年了——通常被叫做「遊戲圖(game graphs)」 。但隨著多重計算範式的出現,現在有一些更一般的概念可以應用於這些結構。反過來,理解這些結構與遊戲和謎題的關係可以提供關於多路圖新層次的直觀和熟悉的理解。
我在這裡的具體目標是,使用我們一直在發展的研究多重計算系統的一般方法,來足夠系統性地研究一系列眾所周知的遊戲和謎題。就像是在與日常事物相關的研究中通常會出現的那樣,我們會遭遇各種具體細節。雖然這些細節可能不會立即被關聯到更大尺度的討論,但對於為我們提供實際遊戲和謎題的現實且可聯繫的畫面來說,它們是很重要的,這也能使我們與多重計算的聯繫有了一個堅實的基礎。
值得一提的是,將遊戲和謎題與物理學聯繫起來的可能性,如果沒有我們的「物理學計劃」(Wolfram Physics Project,校注:項目的官方文章中的描述:「我認為我們已經找到了一條通往物理學基礎理論的道路」),就基本上很難理解。
因為遊戲和謎題通常在某種最根本層面上是離散的——特別是在它們涉及離散的可能性分支的方面。而如果我們假設物理學從根本上是連續的,那麼就沒有理由期待它與遊戲和謎題會有聯繫。但我們的「物理學計劃」的一個關鍵想法是,物理世界在最低層次上是離散的——就像遊戲和謎題一樣。並且更重要的是,我們的「物理學計劃」認為,物理學就像遊戲和謎題一樣,有離散的可能性可探索。
我在這裡討論的每一個遊戲和謎題,在結構和操作(operation)上,一開始都可能顯得相當不同。但我們將看到的是,當以一種多重計算的視角來看時,在我們不同的例子中,存在著顯著的、幾乎是千篇一律的統一性(uniformity)。在文本結尾的部分,我會開始討論各種重要的多重計算現象如何在遊戲和謎題的背景中起作用,在此之前我不會過多地評論這些現象的意義。我也會在最後討論用簡單直接的人類語言對多重計算進行概念化是何等困難——而正是它從根本上導致了遊戲和謎題的迷人特性。
井字棋
Tic-Tac-Toe
考慮在一個2×2的棋盤上玩一個簡化版的井字棋(tic-tac-toe)(又稱「圈叉遊戲 (noughts and crosses)」)。
假設 X 先下。那麼我們可以下用圖來表示可能的棋步:
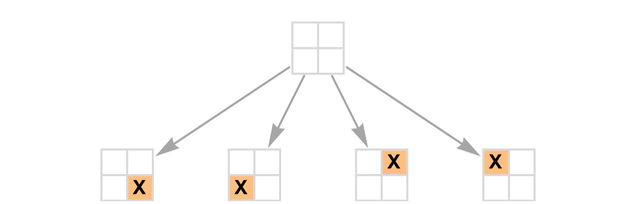
再考慮下一回合的棋步,就得到:

到目前為止,這個圖是一個簡單的樹結構。但如果我們再玩一個回合,我們會發現不同的分支可以合併,「玩到棋盤填滿了為止」,我們會得到一個下圖這樣的多路圖,或「遊戲圖」:
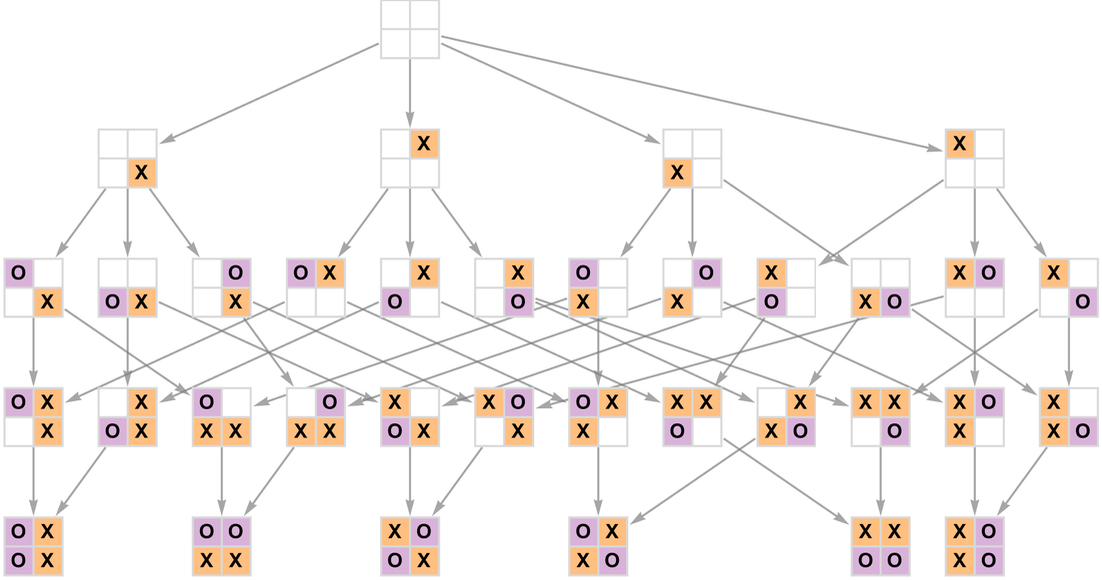
這個圖中的每一條路徑都表示一個可能的完整遊戲:

根據目前的遊戲設定,在任何遊戲中可以達到的棋盤局面配置的總數(即圖中的節點總數)為35,而可能的完整遊戲總數(即從圖的根部開始的可能路徑數)為24。
如果將該圖渲染成3維,可以看到它有一個非常規則的結構:
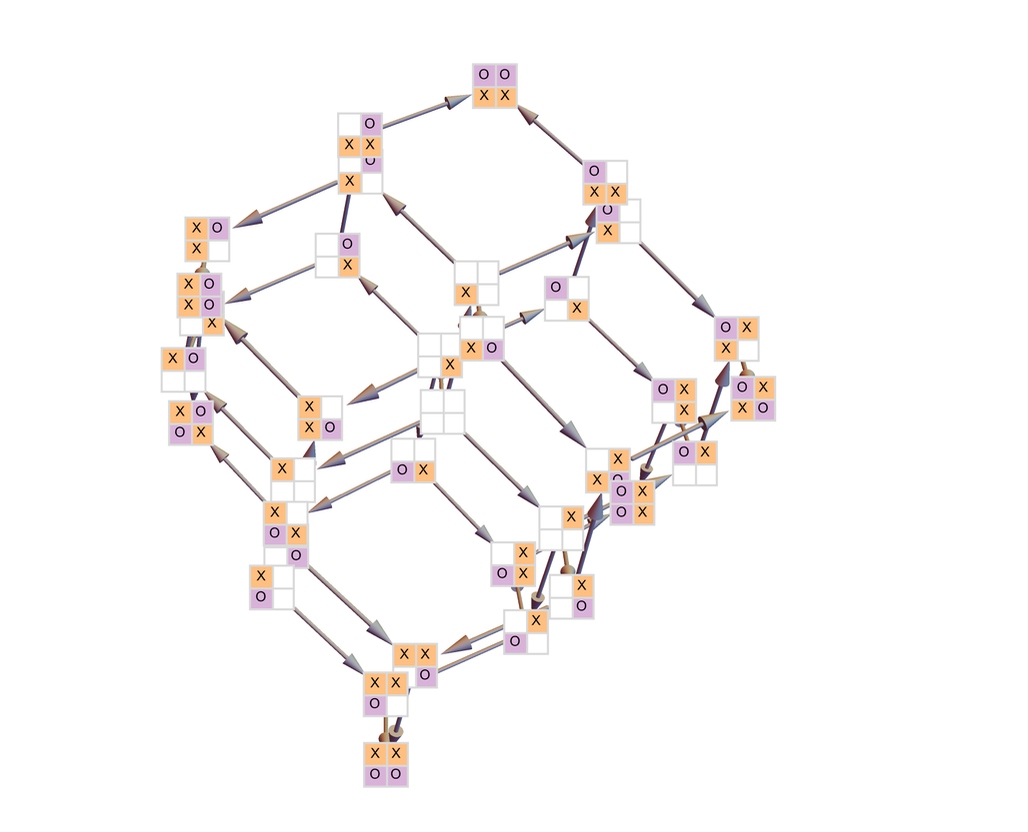
而現在,如果我們把「獲勝」的 2×2 井字遊戲局面定義為在一橫行中有兩個相同的元素,那麼我們就可以在這個多路圖上標註獲勝局面——也就是去掉那些「遊戲已經結束」的情況。
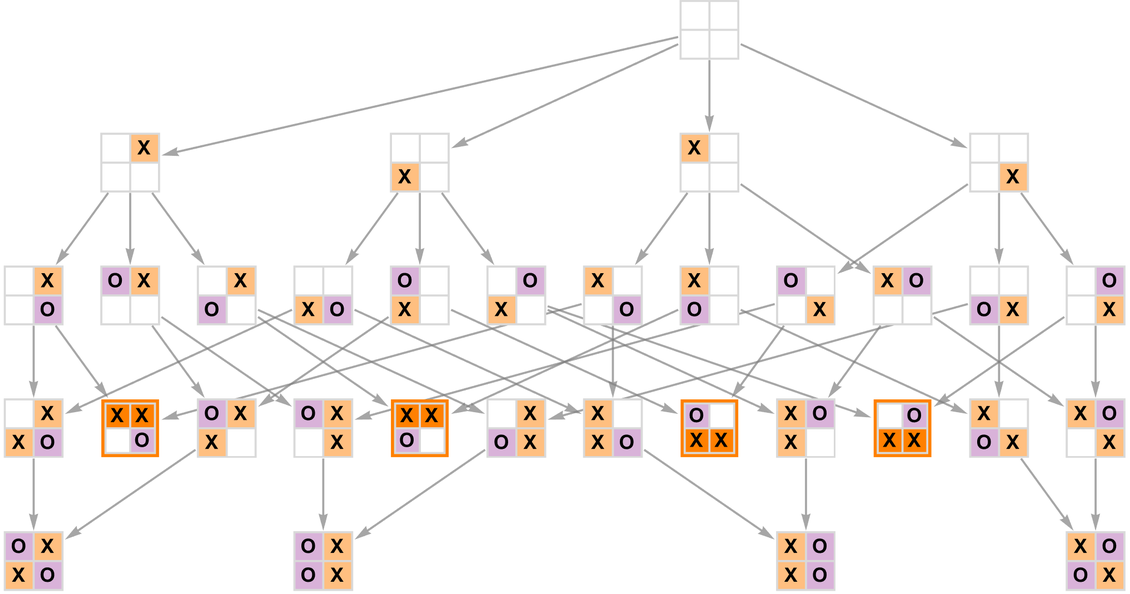
多路圖的大部分核心結構實際上已經很明顯了,即使這在「單人井字棋」這種看似不起眼的情況下,在這種情況下,人們只是在逐步填滿棋盤上的格子:
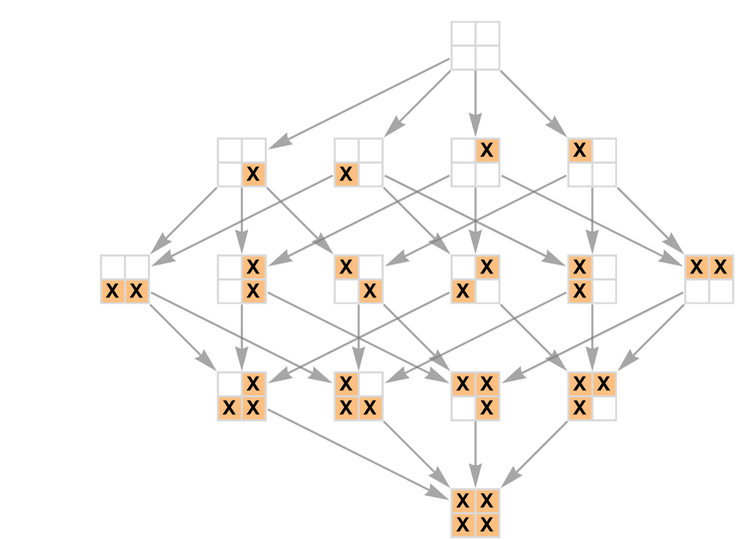
但是,並不那麼不起眼的是,存在著引向同樣棋盤局面(state)的不同路徑。
以不同的方式展示後的這個圖(有2^4 = 16 個節點和 4! = 24 條「遊戲路徑」)具有明顯的4維超立方體形式(現在我們沒有寫出了每個各自中的明確X符號):

對於一個3×3的棋盤,這個圖會是一個9維的超立方體,有2^9=512個節點和 9!=362880 條「遊戲路徑」,以「棋步分層」的形式表示如下:
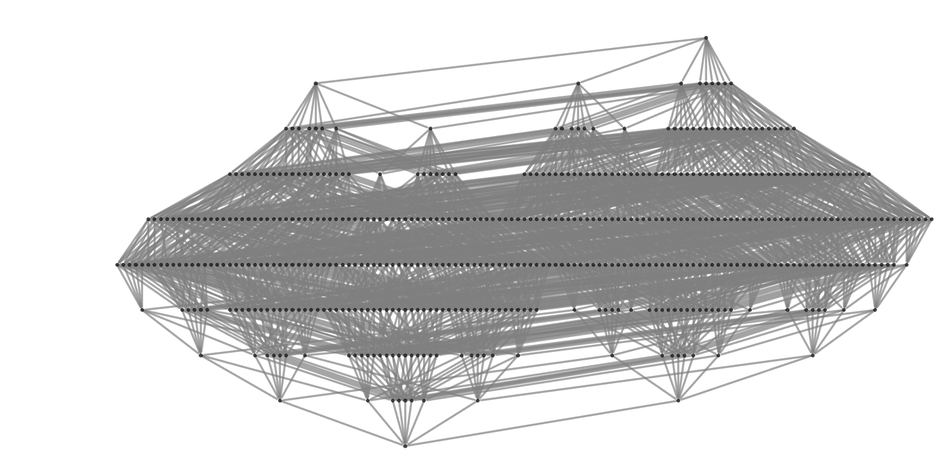
這種基本結構在「單人1維井字棋」中已經可見,其中「長度為 n」的棋盤的多路圖正好對應於一個n維的超立方體。
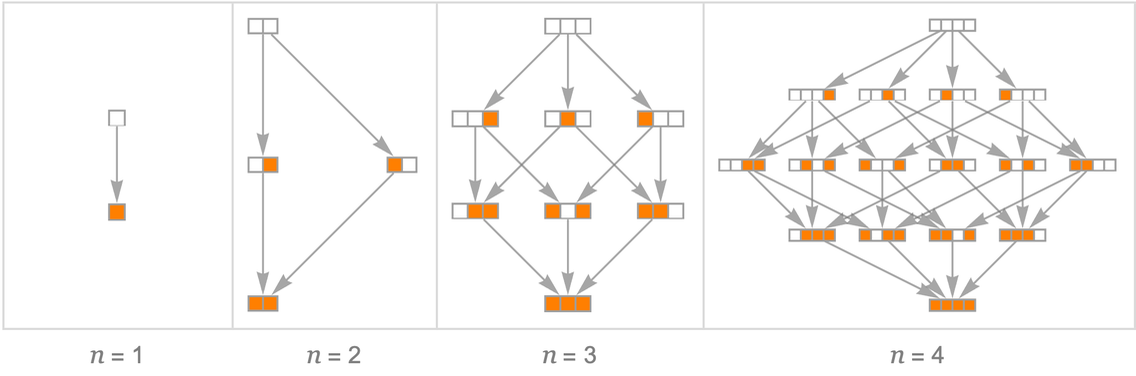
在這種情況下,不同的棋盤局面的總數就是2n,而不同的「遊戲」過程的數量是n!。在第t步,不同棋盤局面(即狀態)的數量是二項式係數[n, t](Binomial[n, t]) 。
如果是2個玩家,圖會變得稍微複雜一些。
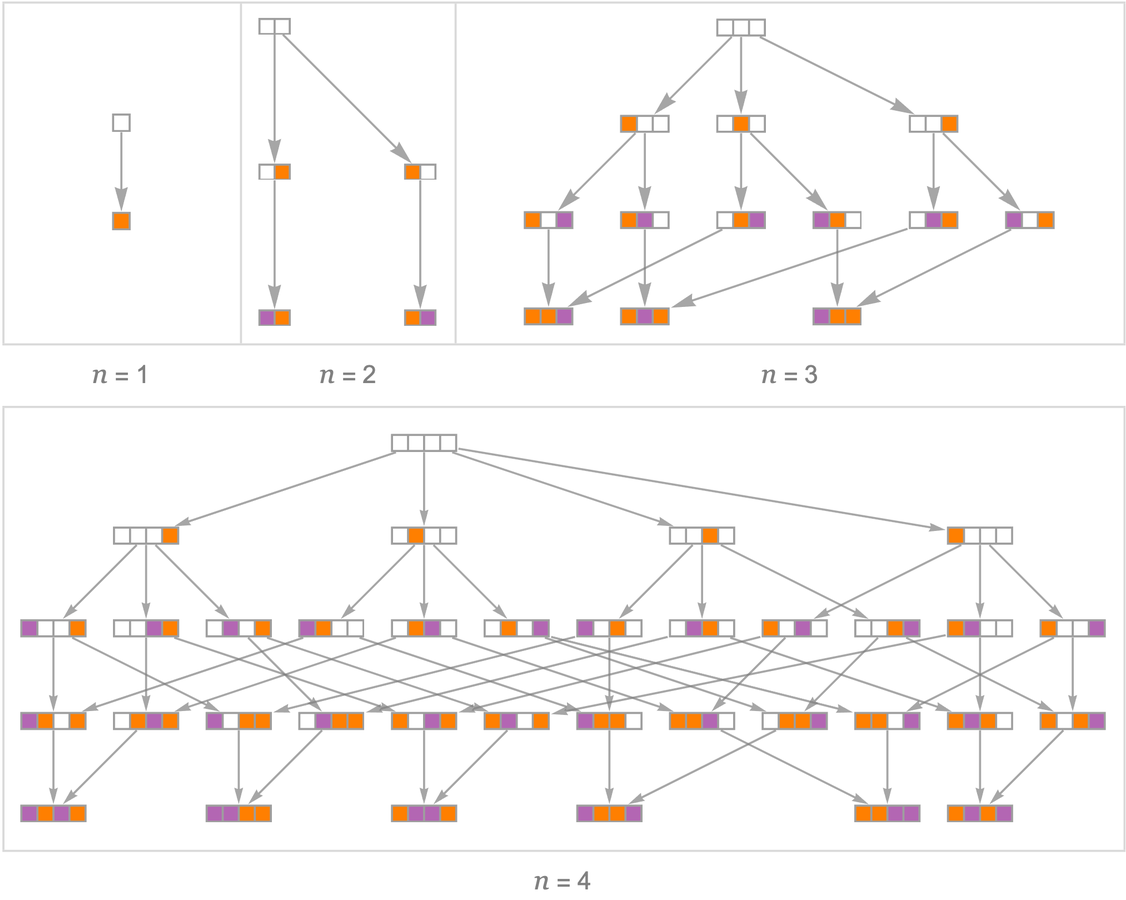
這些圖中的狀態總數是
當n值趨近無窮時,圖中的狀態總數達到

譯註:如果把上式中的n換成n+1,會發現代入後得到的結果很接近長度為n時的狀態數,但將n推向無窮時,n+1可以等同於n。
(注意,對於n=4,其結果與上面討論的2×2棋盤相同。)當遊戲進行到第t步時,不同狀態的數量由以下公式給出
譯註:上面兩個二項式係數相乘

好的,那麼標準的2人3×3井字棋遊戲呢?
它的多路圖在最開始是:

經過兩步(即X和O各走一步),圖仍然是一棵樹(初始狀態現在在中心):

三步之後,狀態開始可以合併了。

而繼續進行全部九步,完整的、有6046個狀態的分層圖是:

一般來說, 在各個步驟時的連通子圖(connected components)的部分的數量如下:
在這個圖的層面上,其結果與總共有9方格的2人1維版本完全相同。但是對於實際的2維3×3井字棋來說,還有一個額外的概念:贏得遊戲,從而終止遊戲。在通常的規則下,當一個玩家在一個水平、垂直或對角線的三個格子上下了棋子時,就被認為是贏了遊戲,比如說:

每當達到像這樣的「獲勝狀態」時,遊戲就被認為是結束了,因此多路圖中的後續狀態就可以被刪減,而之前的6046個節點圖就會變成5478個節點圖。
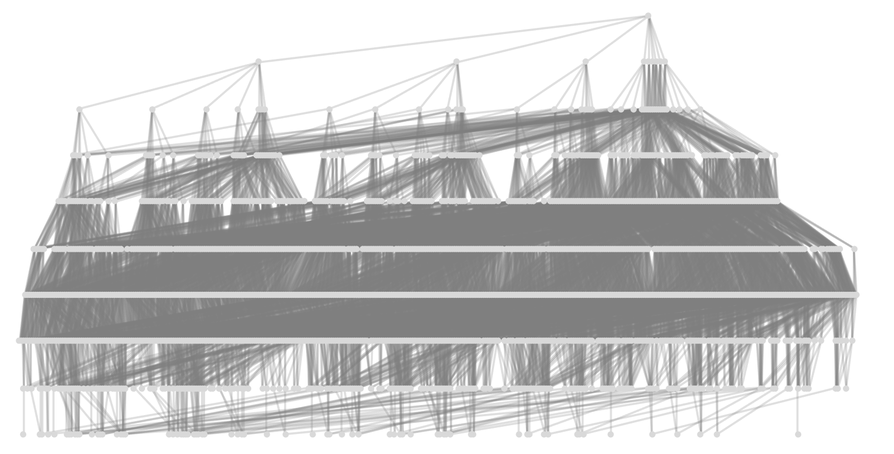
下面是這568個被修剪掉的狀態的例子(其中標記了終止遊戲的「勝利 」)。

遊戲勝利可以發生在不同的步數:從第5步到第9步間都可能有玩家獲勝。不同的勝利狀態總數如下

(任意步驟中,X有626種可能的勝利狀態,O有316種可能的勝利狀態)。
在每一個方格都被填滿之前,人們無法明確判斷一盤棋是否已經以平局結束——只有16種最終的「平局狀態」可以達成。

我們可以在完整的修剪過(game-over-pruned)的多路圖上標註出勝利和平局的狀態。
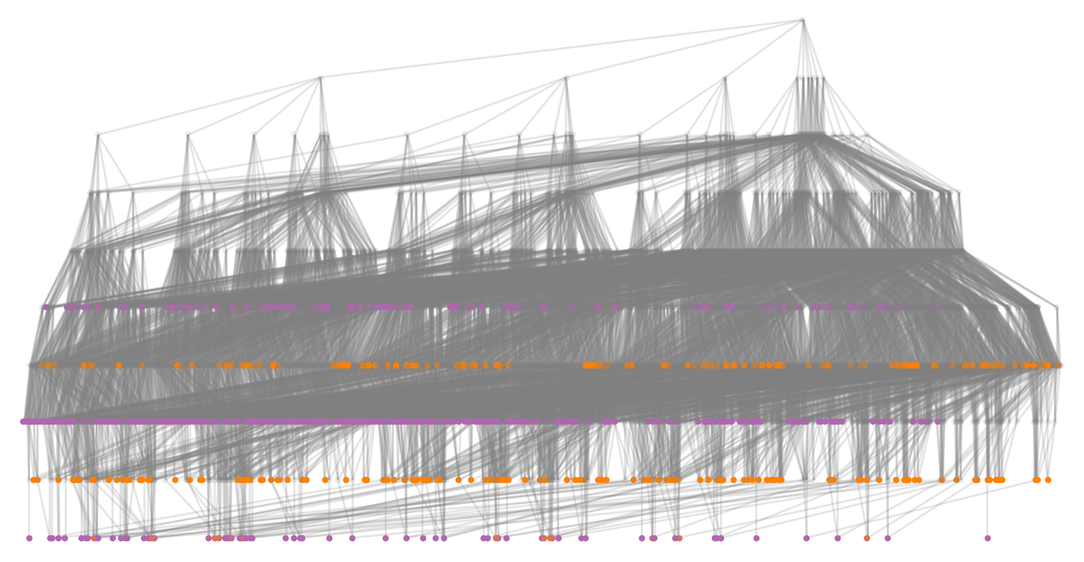
為了進一步研究這個問題,讓我們先看看一個只包括「終局」的子圖,這個子圖從一個已經填滿了4個格子的棋盤開始。
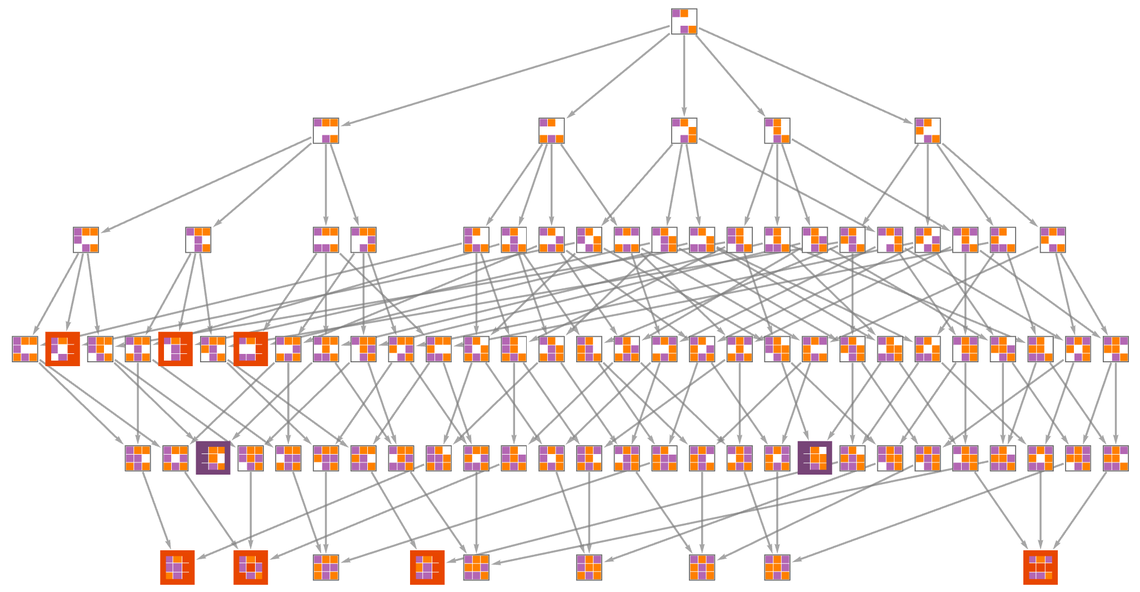
我們在這裡看到,從我們最初的棋盤狀態開始,

X和O都有可能最後獲勝

但在許多這樣的情況下,結果在實際勝利發生前一步或更早的時候就已基本確定了——從這個意義上說,除非某個玩家「犯錯」,否則他們是有必勝策略的(force a win)。
因此,舉例來說,假設現在輪到X了,並且狀態是:

那麼,只要X按以下方式落子,就能保證獲勝:

我們可以通過給多路圖中的子圖(或實際上的「光錐」)著色來標記這種已經註定的勝利局面:
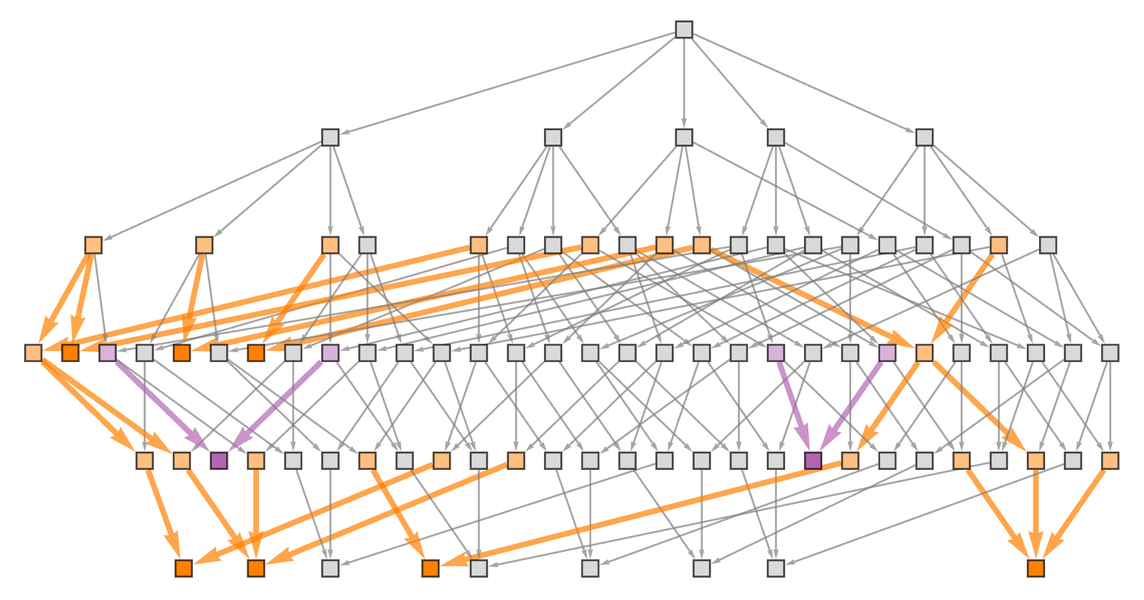
在遊戲最開始,當X下第一步棋時,還沒有任何一方的勝利是已經確定的。但只下了一步棋,就已經有可能達到X有必勝策略的局面:

從第一步後得到的狀態開始,我們可以看到,兩步後有一些棋盤狀態,其中O有必勝策略:
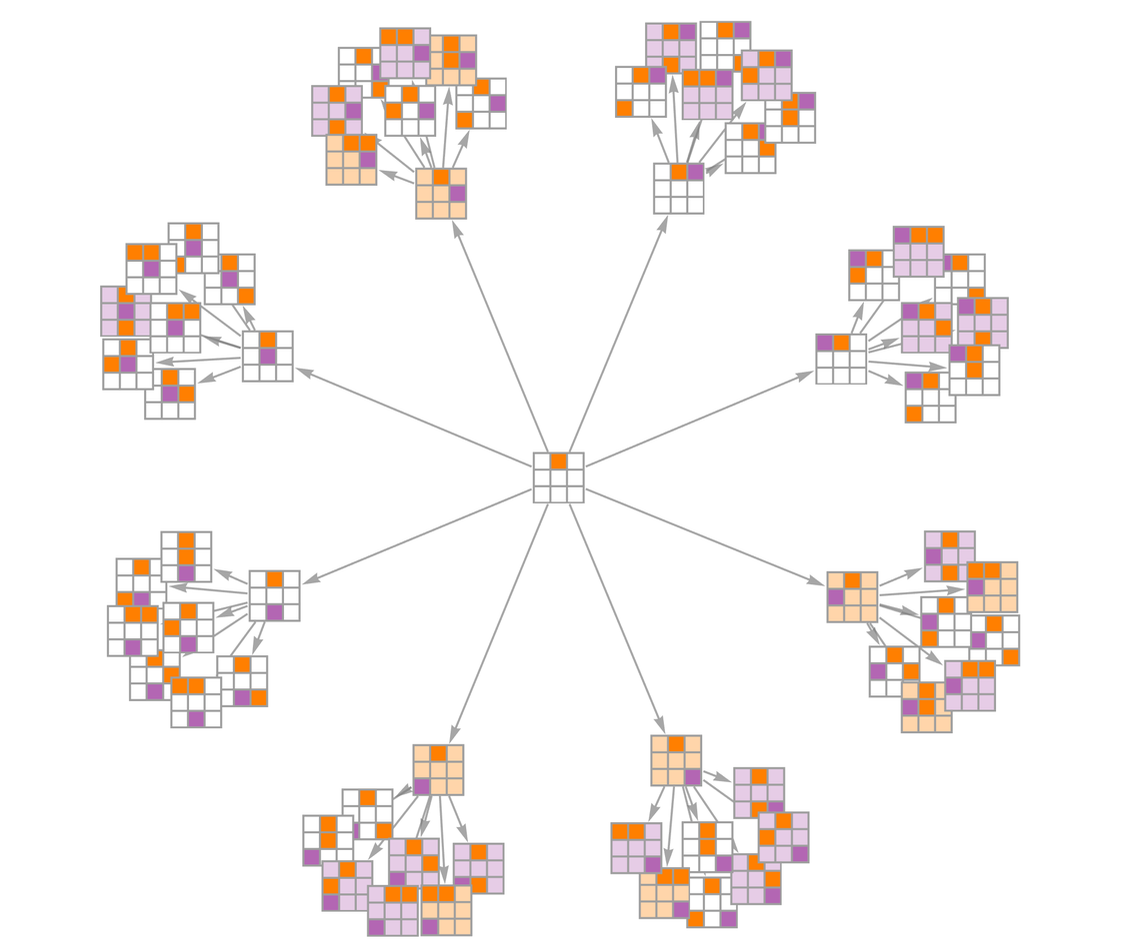
走更多步,就會產生更多的這種某一方有必勝策略的棋盤狀態:
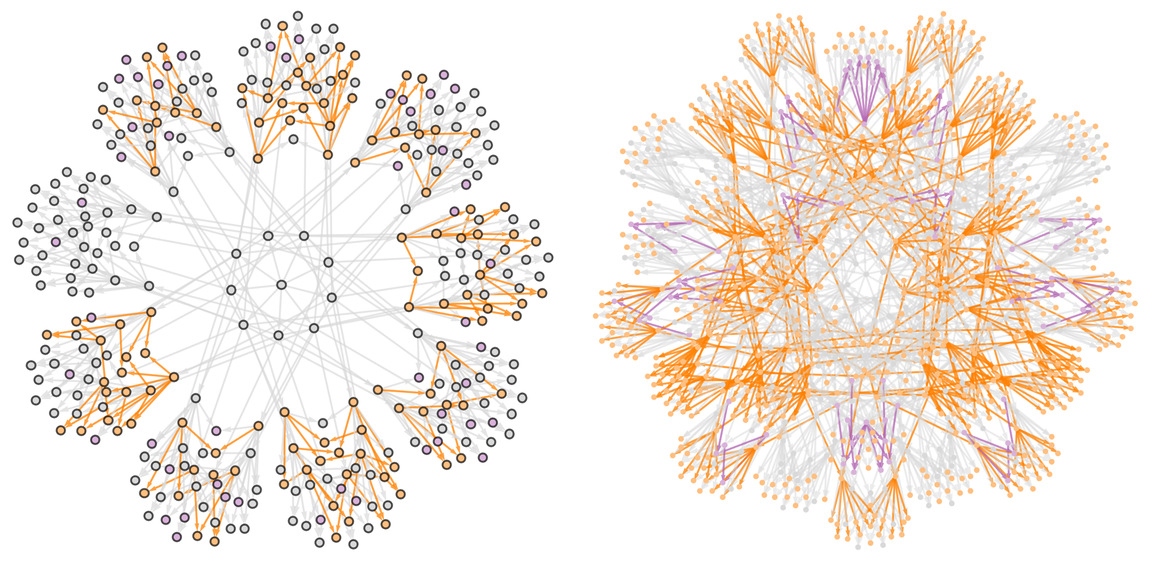
標註整個多路圖,我們就能得到:
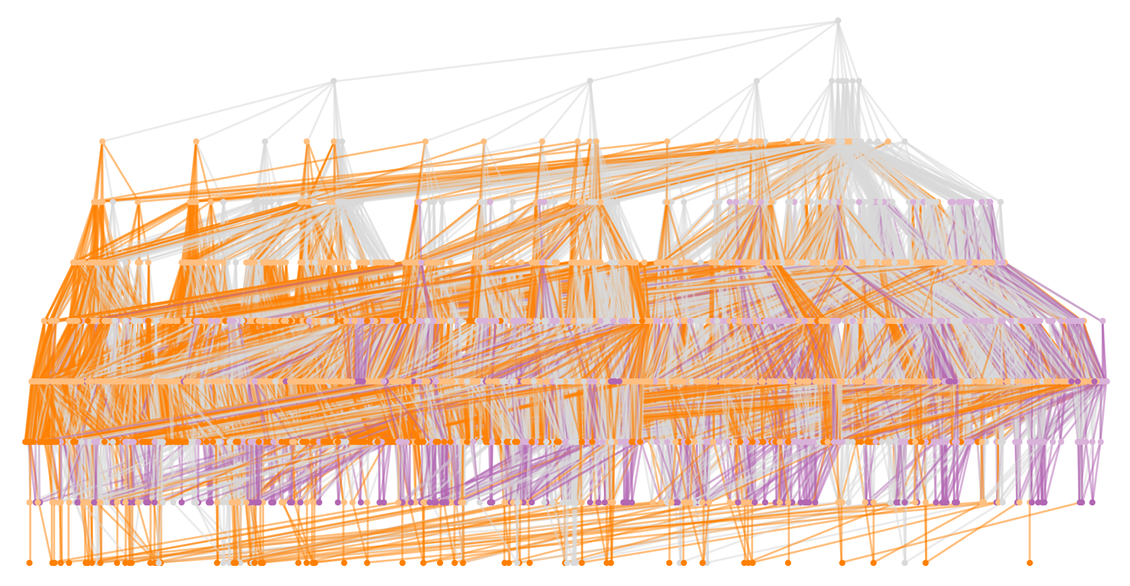
我們可以把這個圖看作是在表示這個遊戲的「解(solution)」:給定任何狀態,圖中的著色告訴我們哪個棋手可以從該狀態中確保勝利,且圖中給定了他們可以怎麼下來達到這樣的狀態。
下圖總結了每一步棋的可能棋盤狀態:

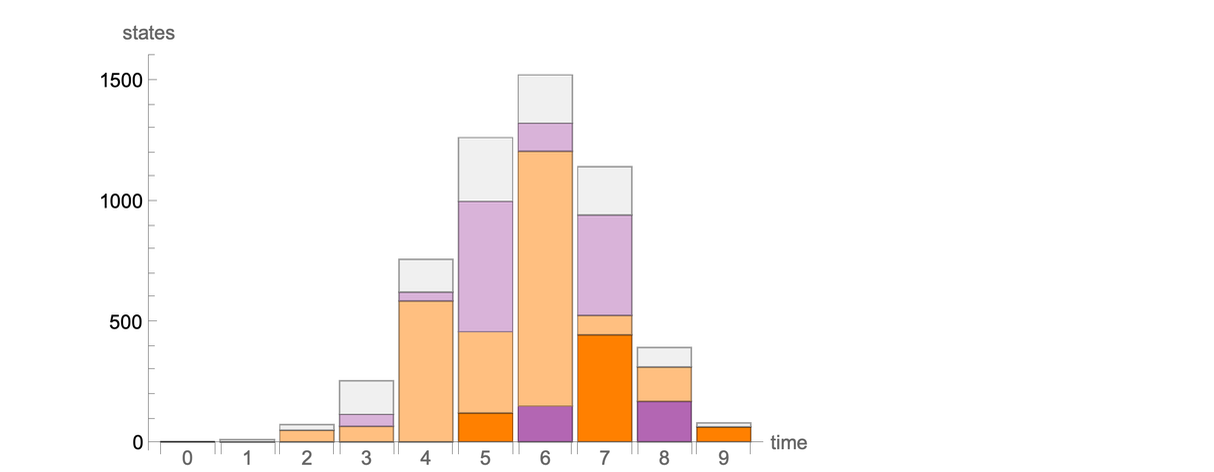
這裡我們只是在計算每一步的各種可能狀態的數量。但是,能否把這些狀態看作是以某種方式分佈在「遊戲狀態空間」(game state space)中的某種東西?
分支圖(Branchial Graph)提供了一種可能的方法來做到這一點。某一特定步驟的基本分支圖是通過連接在前一步驟中具有共同前置狀態的狀態對而得到的。對於2人2×2井字棋的情況,我們在連續的步驟中得到的分支圖如下:
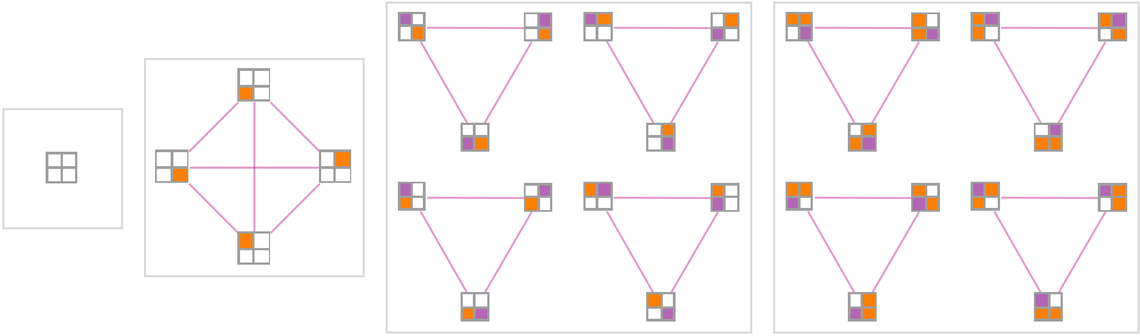
對於普通的3×3井字棋來說,這個分支圖更加複雜。但由於前兩步的多路圖純粹是一棵樹,這些步驟的分支圖仍有一個相當顯而易見的結構。(校注:我的通俗理解得到了厭氧菌的鼓勵,就是等於是把原來的多路圖做垂直剖面,類似你把多簇的花菜剖開,看到每一個段落上的共時的面)

一般情況下,連續步驟下的強連通子圖數量如下表:

以及這些通過不同圖的結構形態分解如下:

下面是其中一些步驟的典型分支圖中子圖的更具體的形態:

在某一特定步驟的分支圖內,不同的組成部分中可能有不同數量的贏局。
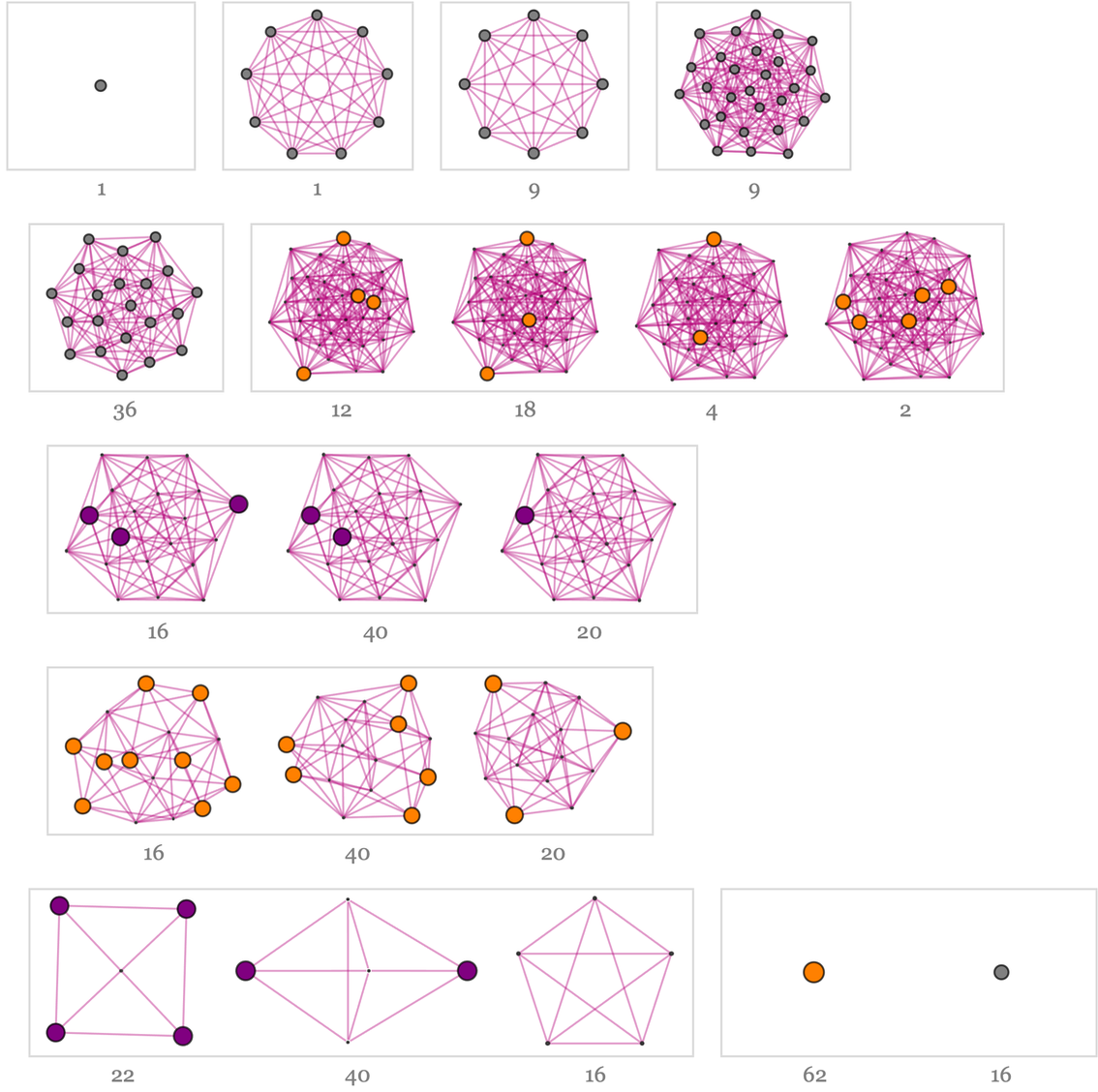
值得注意的是,贏局在各分支圖中的分佈相當廣泛。而這在某種意義上也是井字形遊戲不(那麼)簡單的原因。如果只需知道自己處於分支圖的哪個部分,而就能立即知道結果,那麼遊戲中的「懸念」就會更少。但是在整個分支空間的廣泛分佈下,「大致知道你在哪裡」對確定你是否會贏沒有什麼幫助。
到目前為止,我們一直在討論可以達到什麼狀態,但沒有討論「多經常」會達到這些狀態的。想象一下,我們不是在玩一個特定的遊戲,而是在每一步都以相同的概率進行每一種可能的下子。井字棋的設置是對稱的,在遊戲的大部分時間裡,每個可能的局面在給定的步驟中出現的概率都是相等的。但是一旦開始有「獲勝」,並且有一個「錐形」的「遊戲結束剪枝(game-over-pruned)」的狀態,那麼剩下的狀態就不再有相等的概率。
對於標準的3×3井字棋來說,這種情況發生在7步之後,其中有兩類狀態,其發生的概率略有不同:

在遊戲結束時,有幾類具有不同概率的最終狀態:
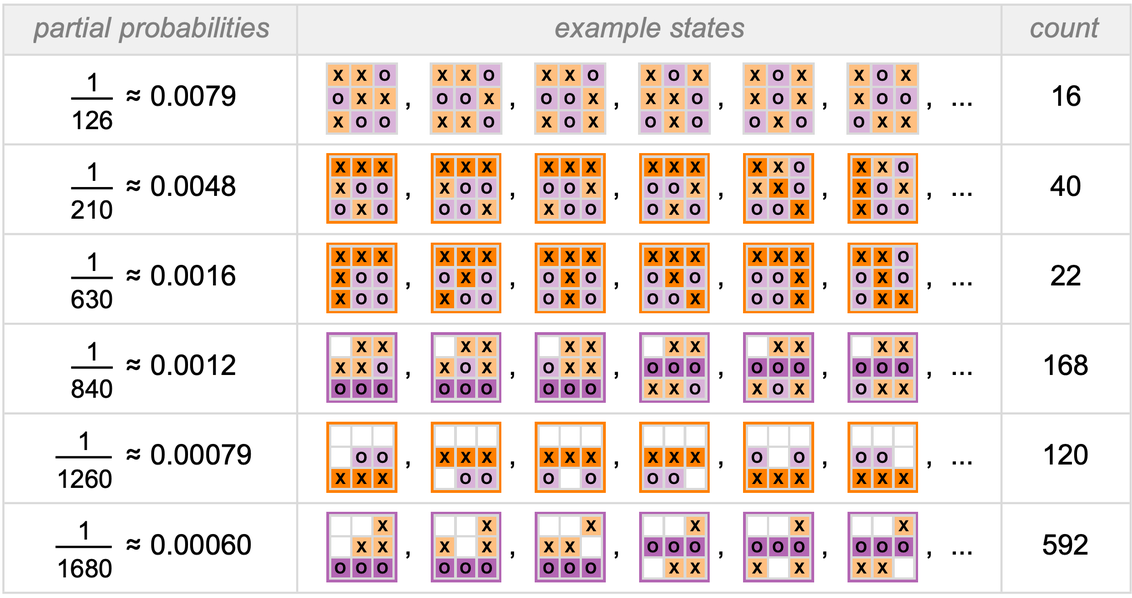
而下圖展示了這對於遊戲的不同結果的概率意味著什麼:

並不出乎意料的是,先下的棋手在獲勝上有優勢。也許更令人驚訝的是,在這種「無策略」的遊玩中,平局是比較少見的——儘管如果一個玩家積極地試圖阻止另一個玩家,他們往往會迫使遊戲走向平局。
我們已經研究了「經典井字棋」和一些特定的變體。但最終還有各種可能的變體。一種來表示任何類似井字遊戲的「棋盤」的方便的一般方法是,給出一個「扁平化」的數值列表—— 0 代表空白位置,i 代表玩家 i 添加的一個符號。
在標準的「二維表示法」中,人們可能會有這樣一個棋盤

將它扁平化後得到:
然後可以表示出典型的獲勝模式:

其中,在每一種情況下,我們都標出了跟獲勝相關的「獲勝符號」,然後給出它們在扁平化列表中的位置。在普通的井字棋中,很明顯,「獲勝符號」的位置必須總是形成一個等差數列。而概括井字棋的一個好方法似乎是將 i 的勝利定義為與 i 的符號出現在形成一定長度s的等差數列的位置有關。對於普通的井字棋來說,s=3,但一般情況下,它可以有其他值。
現在考慮一個長度為5的列表(即5個位置的「1維棋盤」)的情況。完整的多路圖如下,其中長度為s=3的等差數列的「獲勝狀態」被標出了。
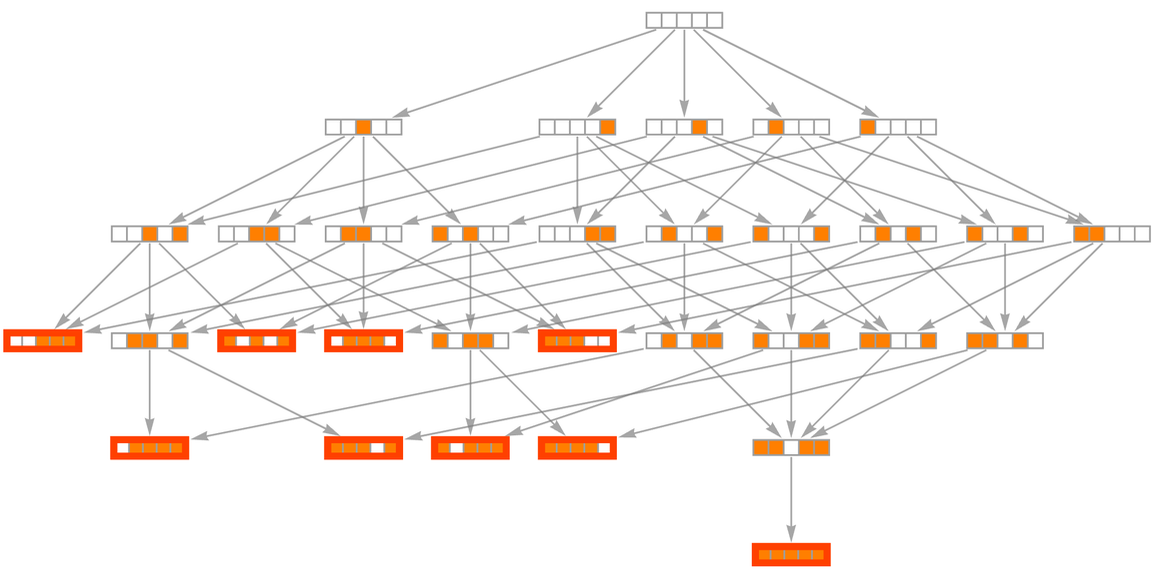
上圖的一個更具對稱性的可視化是:
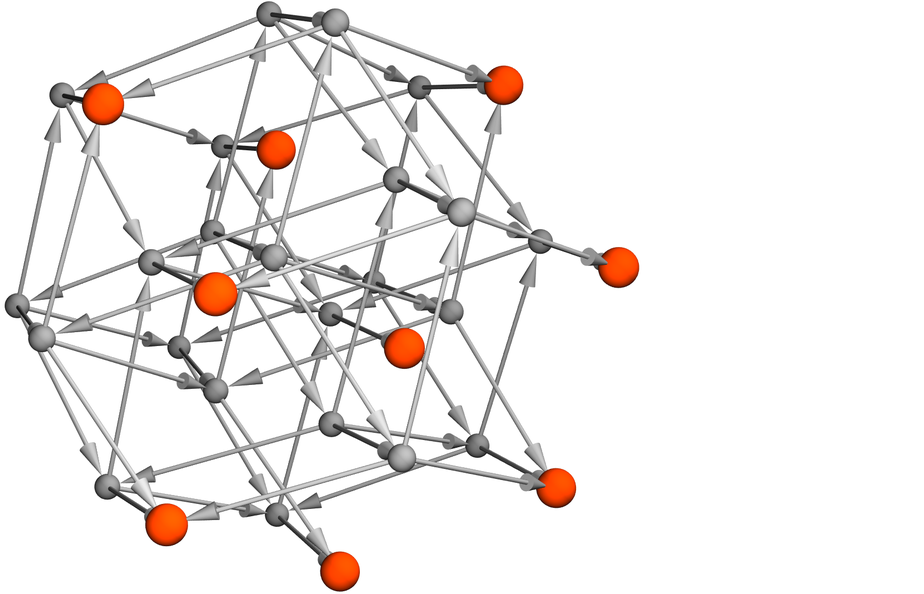
下面是長度為7的1維棋盤和2個玩家的情形的類似結果:
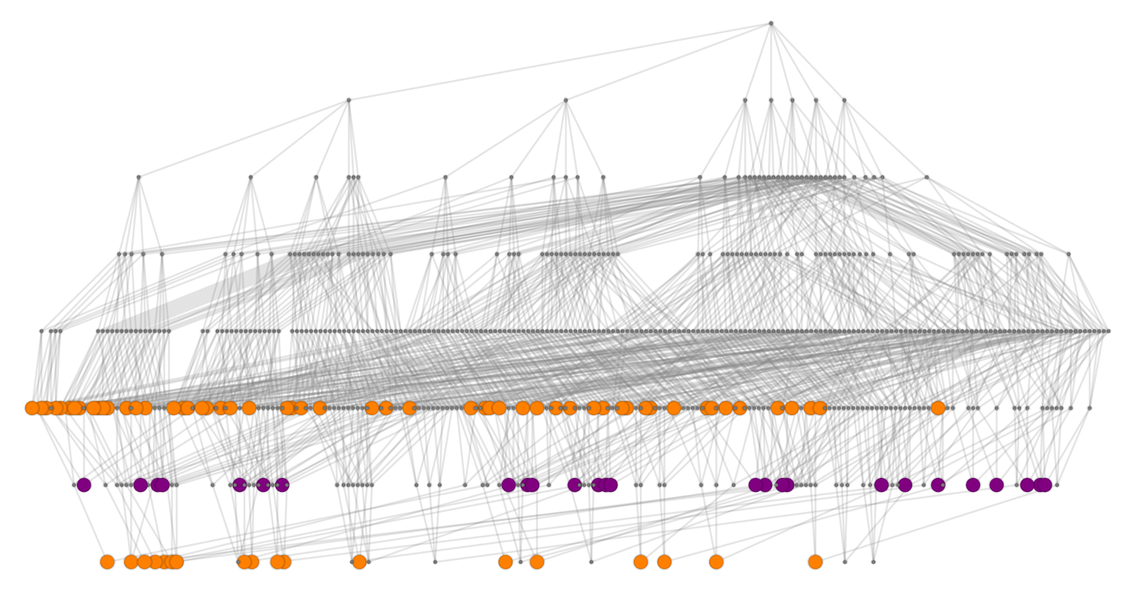
對於每個大小的棋盤n,我們可以計算出任何特定玩家的獲勝狀態總數,以及總的狀態數。當獲勝是基於長度為3的算術級數(即s=3)時,其結果是:

這裡的兩個玩家、n=9(=3×3)的情況與普通井字棋相似,但不是完全一樣。
特別是,像這樣的狀態

在扁平化了之後,也被認為是X獲勝的狀態,但在普通井字遊戲中卻不是。
如果我們增加勝利所需的等差數列長度,例如增加到s=4,我們就會得到:

遊戲狀態的總數沒有變化,但正如預期的那樣,「獲勝的方式更少了」。
但是,假設我們的棋盤完全被填滿了。對於小棋盤來說,任何棋手不管怎麼下子都可能達不到等差數列,因此遊戲必須被認為是平局——正如我們在n=5的情況下看到的那樣。

但是,最後發現這是一個與拉姆齊理論(Ramsey theory)相關的結果:對於n≥9,不可避免的是,至少有一個玩家會有「等差數列的勝利」,所以永遠不會出現平局——正如下面這些例子所說明的那樣:

行進(Walk)和它們對應的多路圖
Walks and Their Multiway Graphs
(校注:walk 的翻譯作為名詞與動詞,國內有翻譯為途徑,但從 Wolfram 寫作出發點的構想又是非常經典的 random-walk,即隨機漫步或隨機遊走的問題來源,但用於本文中顯得有些過於浪漫化表達,取折中翻譯做「行進」)
像井字棋這樣的遊戲,實際上在每一步都要移動到幾個可能的新棋盤狀態中的一個——我們可以把它看作是在「遊戲狀態空間」中的不同「位置」。但是,如果我們不考慮棋盤狀態,而只是把我們的狀態看作是一個柵格(lattice)上的位置,如:

然後我們看一下這個圖中可能的行進路線(walks),現在這個情況下,每一步都可以向4個方向中的任何一個方向走一個單位嗎?
從圖上某一點開始,1步之後的多路圖很簡單地就是

這裡我們特地佈置了這個圖形,使得「狀態」的位置對應於它們在柵格上的幾何位置。
兩步之後我們得到:
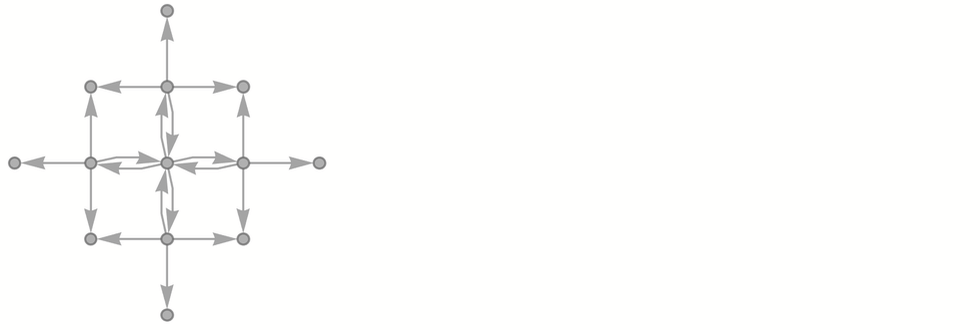
而更一般的情況下,這個多路圖的結構只是「重述」(recapitulates)了柵格的結構。
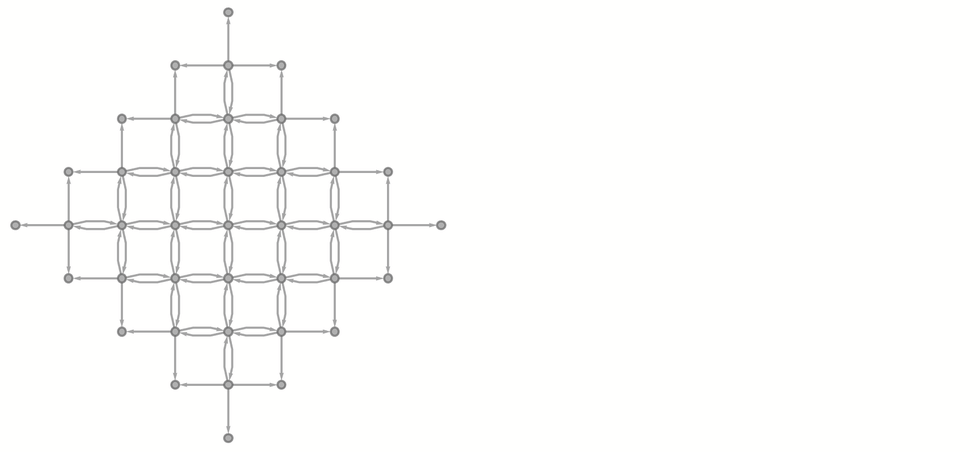
我們可以把多路圖中的路徑,看作是代表柵格中所有可能的一定長度的隨機行進(Walk)路線。我們可以將該圖鋪成3D,垂直位置代表可以到達某一點的第一步:

我們也可以像佈置井字圖的多路圖那樣佈置這個圖:

這些「隨機行進(random-walk)」的多路圖的一個特點是,它們包含循環,記錄了「返回已經去過的地方」的可能性。這與井字棋中的情況不同,在井字棋中,每一步都是在棋盤上增加一個元素,而不可能再回到以前的狀態。

但是我們可以通過考慮「自我回避的行進路線(self-avoiding walks)」,為行進建立一個類似的「永不回頭的規則」,其中任何被訪問過的點都不會被再次訪問。
讓我們首先考慮非常簡單的柵格:

現在用紅點表示「我們目前到達的地方」,用藍點表示我們以前去過的地方,並從一個角落開始:
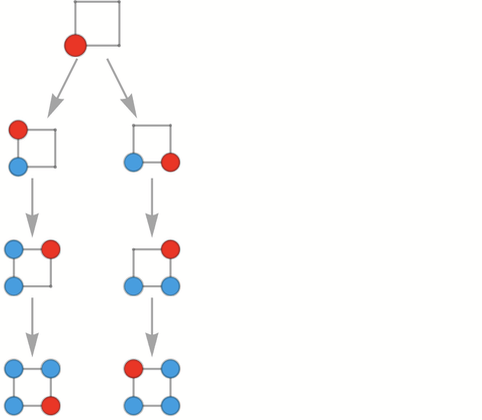
這裡只有兩種可能的走法,一種是順時針走,另一種是逆時針走。如果允許從每個可能的位置開始,就會產生一個稍微複雜的多路圖:
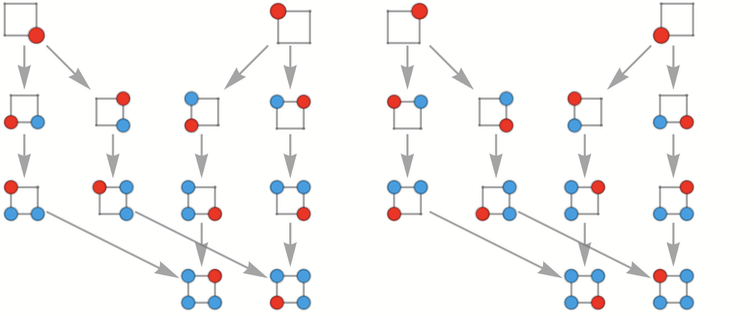
如果是一個2×3的網格,我們就得到下圖:
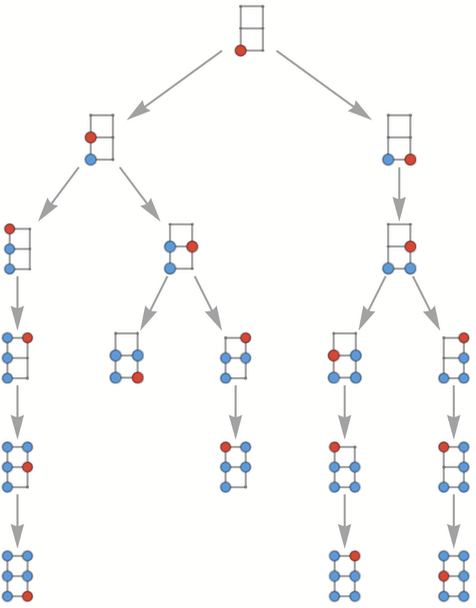
而 3x3 的網格對應的多路圖是:
從中間開始,用不同的佈局來畫多路圖,可以得到:

請注意圖中的幾個大「洞」的存在,其中每一邊的路徑基本上是以「相反的方式」到達「同一個地方」。請注意,在有1個藍點和最多8個紅點的2304種可能方式中,這個多路圖實際只達到了57種。(從角落開始可以達到75種,從所有可能的初始位置可以達到438種)。
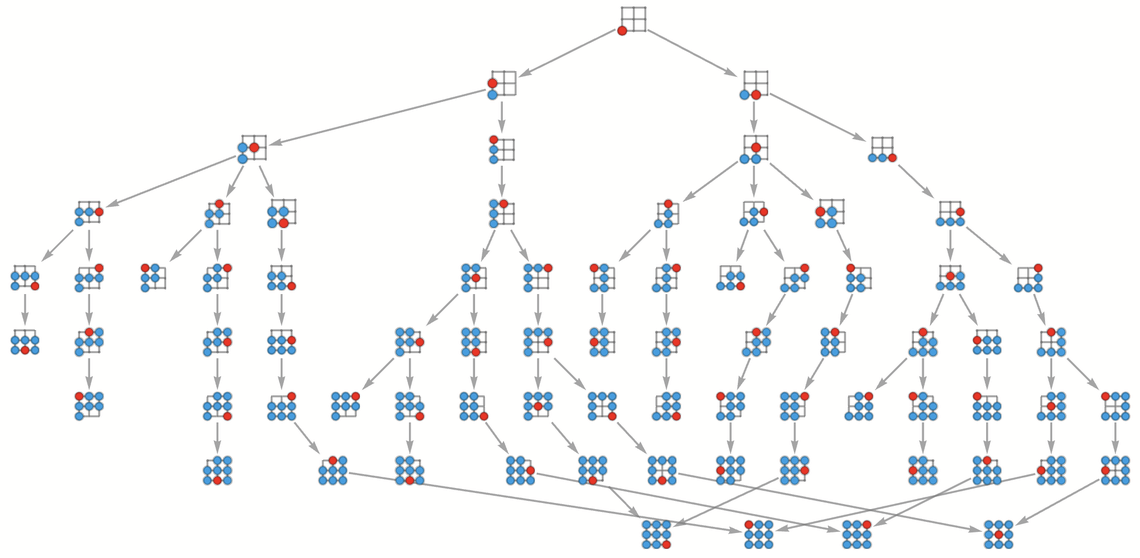
在4×4的柵格里(從角落裡開始走),多路圖有這樣的形態:
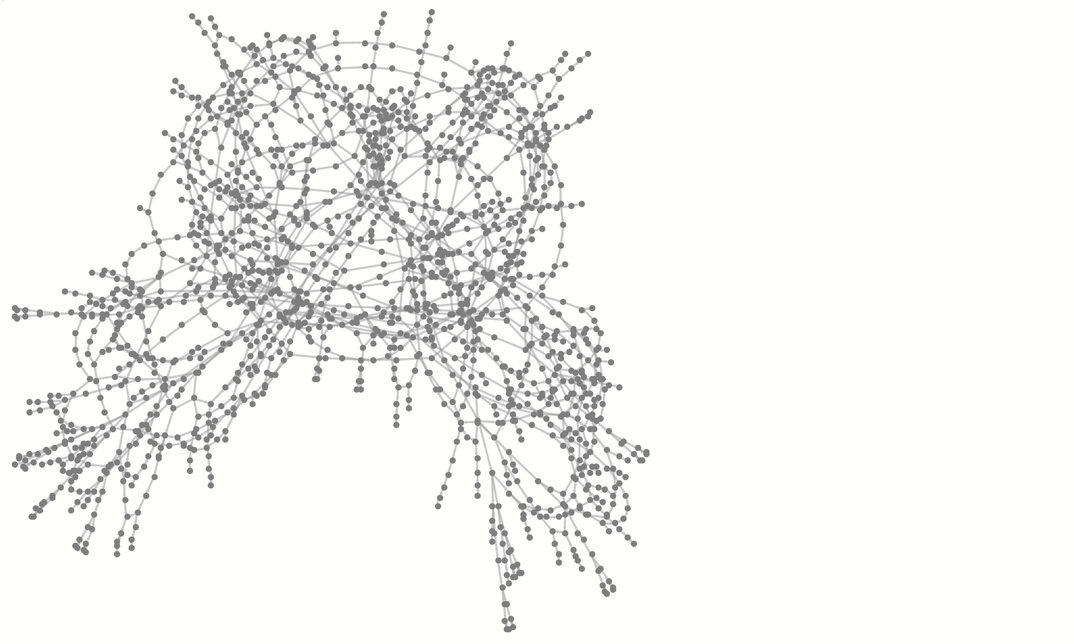
或者換一種佈局:
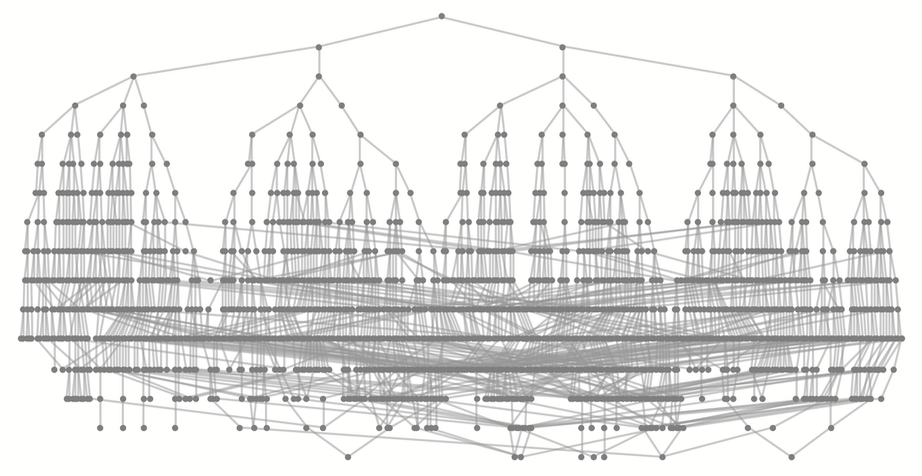
其中,共計524288個狀態中,有1677個狀態最終被訪問到了,每一步訪問(即圖中連續幾層的節點數量)的新狀態的數量為:

對於一個5×5的網格來說,有89,961個狀態能夠達到,根據以下情況分佈在各個步驟中:

(對於一個有n個頂點的網格,總共有n x 2^(n–1) 個可能的狀態,但實際達到的數量總是小得多)。
在討論行進時,一個明顯的問題是關於迷宮的。
考慮下面這個迷宮:

就穿越這個迷宮而言,它等同於在圖上「行進」(walking)。

而另一種表示即是:

但就像以前一樣,代表所有可能的行進路線的多路圖本質上只是「重述」了這個圖。這意味著,「解」這個迷宮在某種意義上同樣可以被認為是直接在迷宮圖或多路圖中找到一條路徑:

十二面體遊戲與其他相關遊戲
The Icosian Game & Some Relatives
我們對自我回避的行進路線的討論,其實與威廉·羅文·漢密爾頓(William Rowan Hamilton)在1857年提出的十二面體遊戲(Icosian game)(這與早期的計算機遊戲 Hunt the Wumpus 有一定的關係)直接相關。


這個「遊戲」(或者更恰當地說,謎題)的目的是在二十面體圖形的邊上找到一條路徑(是的,一條漢密爾頓路徑),訪問每個節點(並返回到它的起點)。我們可以再次構建一個多路圖,代表遊戲中所有可能的「移動」序列。
讓我們從底層四面體圖形的較簡單情況開始:

由此我們得到多路圖:
而考慮進了四面體圖形上所有可能的起始位置得出的「組合的多路圖」,給出了一個呈截斷的立方八面體形狀(truncated cuboctahedron)的多路圖:

按照這個圖形,我們可以看到,從任何初始狀態出發,都有可能達到四面體圖形中的每個節點都被訪問過的狀態。事實上,由於四面體圖是一個完全圖(Complete graph),它甚至可以保證序列中的最後一個節點將與起始節點「相鄰」——這樣我們就形成了一個漢密爾頓環(Hamiltonian Cycle)來解決這個謎題。
對於立方體圖來說,事情就不那麼簡單了:

這時從一個特定的狀態開始的多路圖是:
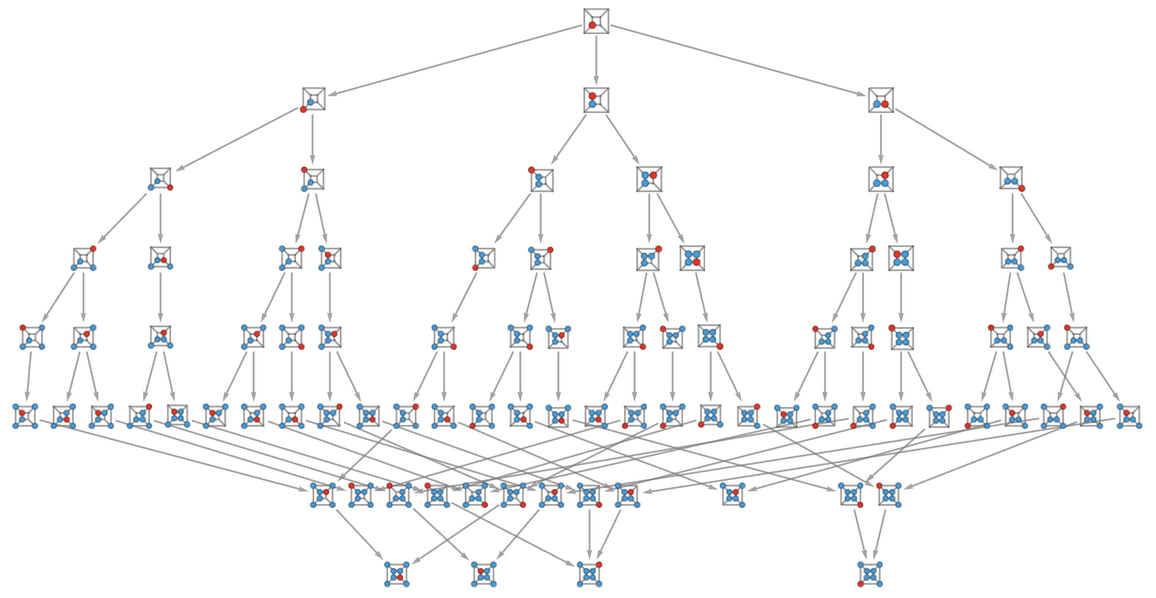
這時就有13個無法產生進一步行動的狀態。

在其中一些情況下,玩家被「堵住」(boxed in)了,沒有相鄰的節點可供訪問。在其他情況下,所有的節點都被填滿了。但只有3個最終實現了真正的漢密爾頓循環,即其終點與起始節點相鄰。

事實證明,人們可以通過4條不同的路徑從多路圖的根部到達這些狀態中的每一個。這種路徑的一個例子是:

我們可以將這一路徑概括為原始立方體圖的漢密爾頓環:

在多路圖中,12條「獲勝路徑」是
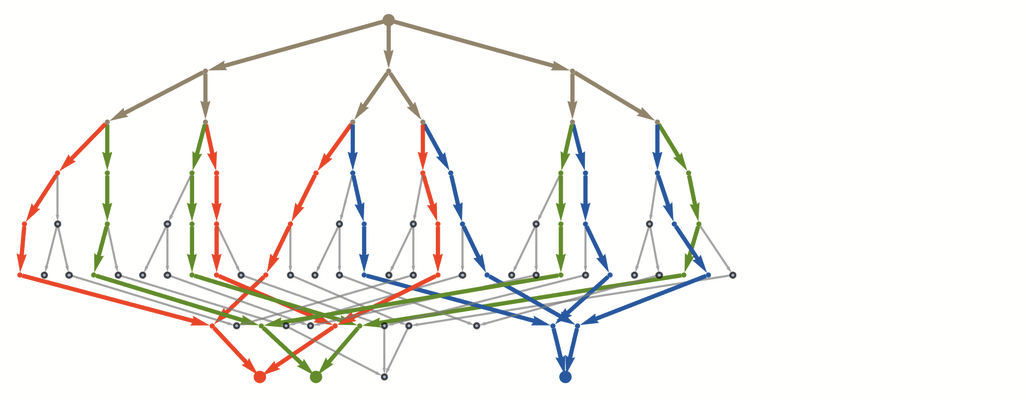
這還可以表示成下圖:

如果只保留「獲勝路徑」,多路圖的子圖具有對稱的形式:

對應於這些獲勝的路徑的底層立方體圖的漢密爾頓環分別是:
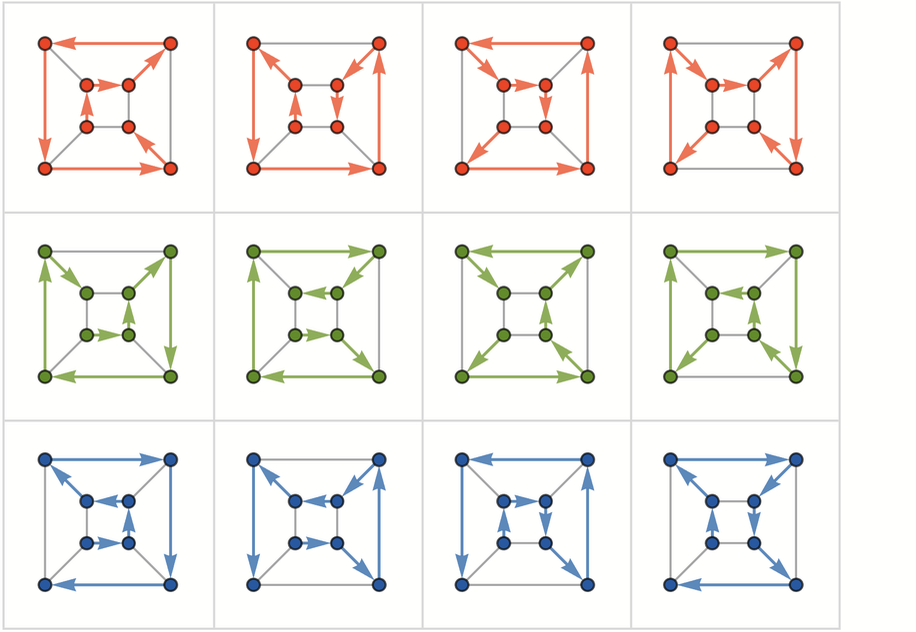
對於十二面體圖(即原本的二十面體遊戲),多路圖更大、更復雜。它開始於:

並在11步之後出現了第一次合併(總共529步),最後總共有11093個節點,其中2446個是「終止狀態」,不可能再有進一步的移動。下圖展示了每個連續步驟中的終止(黃色柱狀圖)和非終止(藍色柱狀圖)狀態的數量:

連續的「走上成功之路」的狀態比例如下,表明從某種意義上說,該謎題在開始時比結束時更難:

有13個「結束狀態」,填補了底層十二面體圖的每一個位置,其中3個對應於漢密爾頓環:

從多路圖的根部通往最終狀態的路徑總數(實際上是也就是嘗試解謎的總數量)為3120條。其中,有60條路徑通向3個漢密爾頓環的最終狀態。這些「獲勝路徑」的一個例子是:

與3個漢密爾頓環結束狀態中的每一個對應的基本漢密爾頓環的例子是:
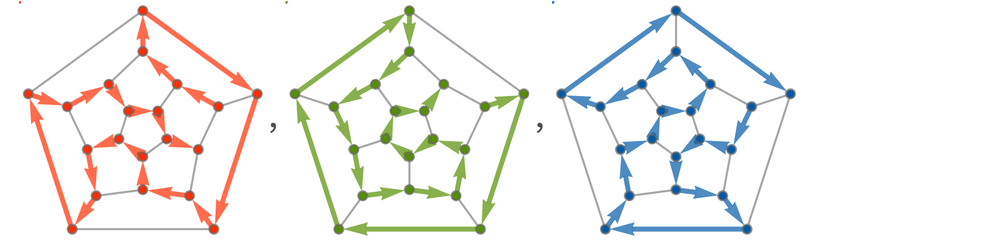
而這展示了通過多路圖到達漢密爾頓環終點狀態的所有60條路徑——從而對應於謎題的解:

實際上,解謎就是在多路圖的所有可能性中成功找到這些路徑。不過,在實踐中——例如在定理證明中——有比直接查看多路圖中的所有可能性更有效的方法來尋找「獲勝路徑」(例如Wolfram語言中的 FindHamiltonianCycle)。但對於我們在多重計算框架中理解遊戲和謎題的目標來說,看看這個謎題的解決方案在多路圖中是如何佈局的是很有用的。
漢密爾頓的十二面體遊戲首次引入了圖上的漢密爾頓環的概念。但早在1736年,萊昂哈德·歐拉(Leonhard Euler)就在柯尼斯堡橋之謎中討論了現在所謂的歐拉環(Eulerian cycles)。

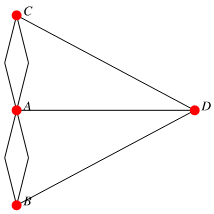
用現代術語來說,我們可以把這個謎題表述為尋找一條能夠訪問一次且只訪問一次圖中所有邊的路徑的問題(其中原謎題中的「雙橋」已經被額外的節點所取代)。

我們可以創建一個多路圖,代表從某一特定頂點出發的所有可能路徑。

但現在我們看到,這裡的最終狀態是:
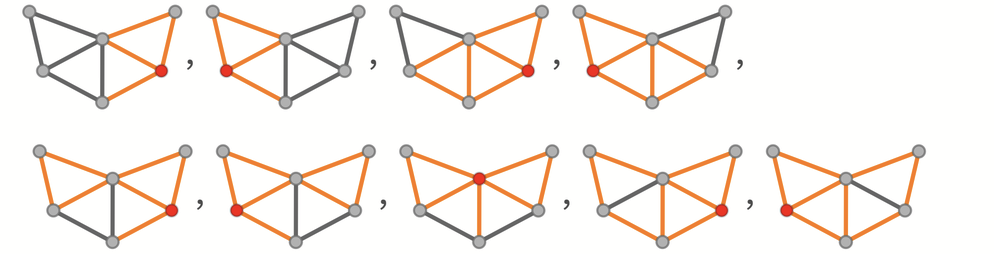
而由於它們都沒有訪問過所有的邊,所以這裡沒有歐拉環。為了徹底解決這個難題,我們需要構造一個多路圖,從所有可能的底層頂點開始。其結果是一個不相連的多路圖,其末端狀態也從未訪問過底層圖中的每一條邊(從每個子圖中的「層次」數量少於10這一事實可以看出)。
地理遊戲
The Geography Game
在地理遊戲中,人們有一組詞(比如說地名),然後試圖將這些詞「串起來」,一個詞的最後一個字母與下一個詞的第一個字母相同。遊戲通常在沒有人能夠想出一個符合規則的、且之前沒有使用過的詞時結束。
通常在實踐中,這個遊戲是由多個玩家遊玩的。但我們完全可以考慮只有一個玩家的版本。作為一個例子,讓我們把我們的「詞」作為美國各州的縮寫。然後我們就可以構造一個什麼詞可以接什麼詞的圖:

首先,讓我們忽略一個州名是否「已經被使用」的問題。然後,從馬薩諸塞州(Massachusetts)開始,我們可以構建一個多路圖的開頭,給我們所有可能的序列。

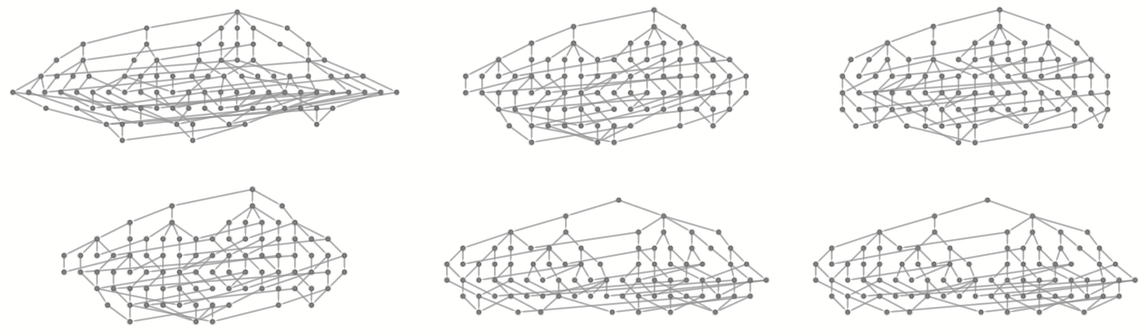
十步以後這個圖變成了:
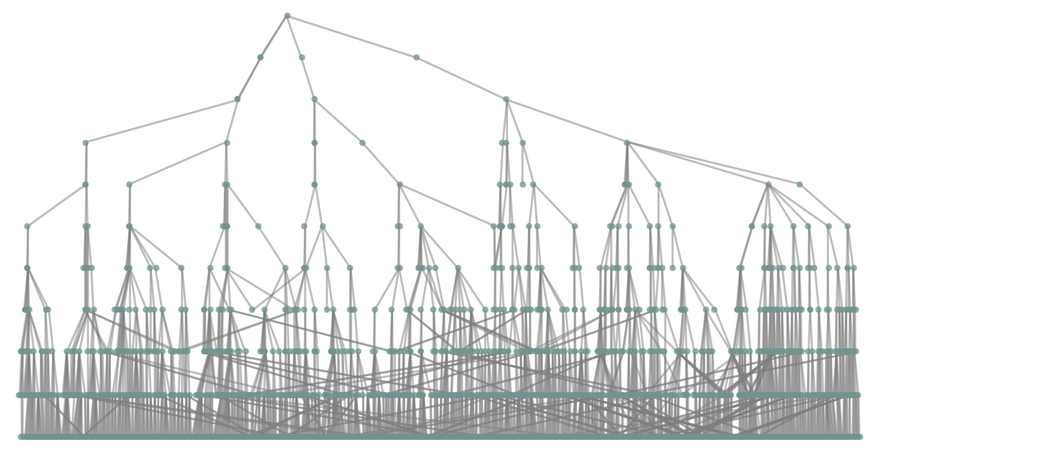
或者換一種佈局:
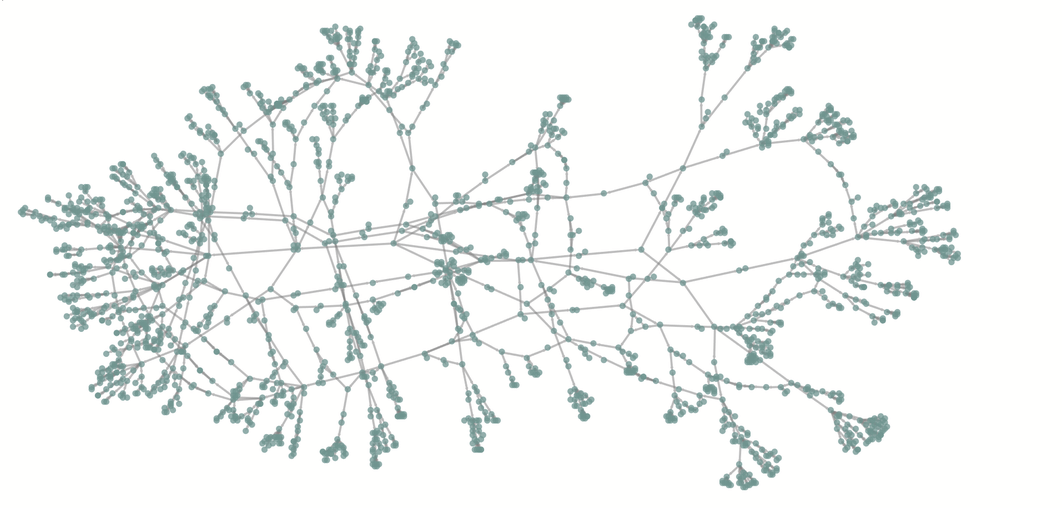
假設不允許任何狀態重複,下面的圖表展示了該圖中的路徑總數與路徑長度的關係。
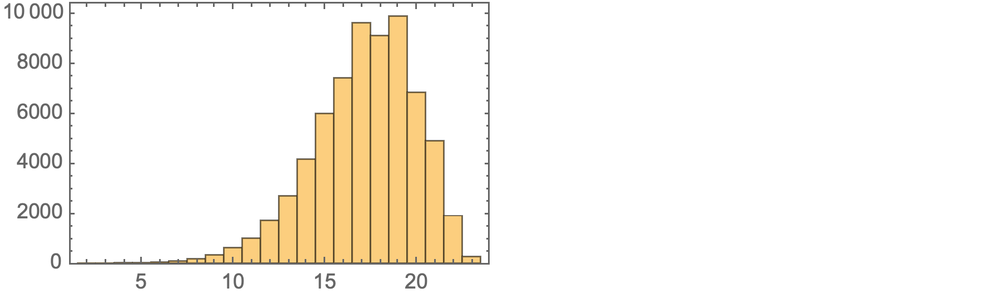
路徑的最大長度是23,有256條這樣的路徑,88條以TX結尾,168條以AZ結尾。幾個這樣的路徑的例子是:

而所有這些路徑都可以用等同於有限狀態機(finite state machine)的形式來表示:
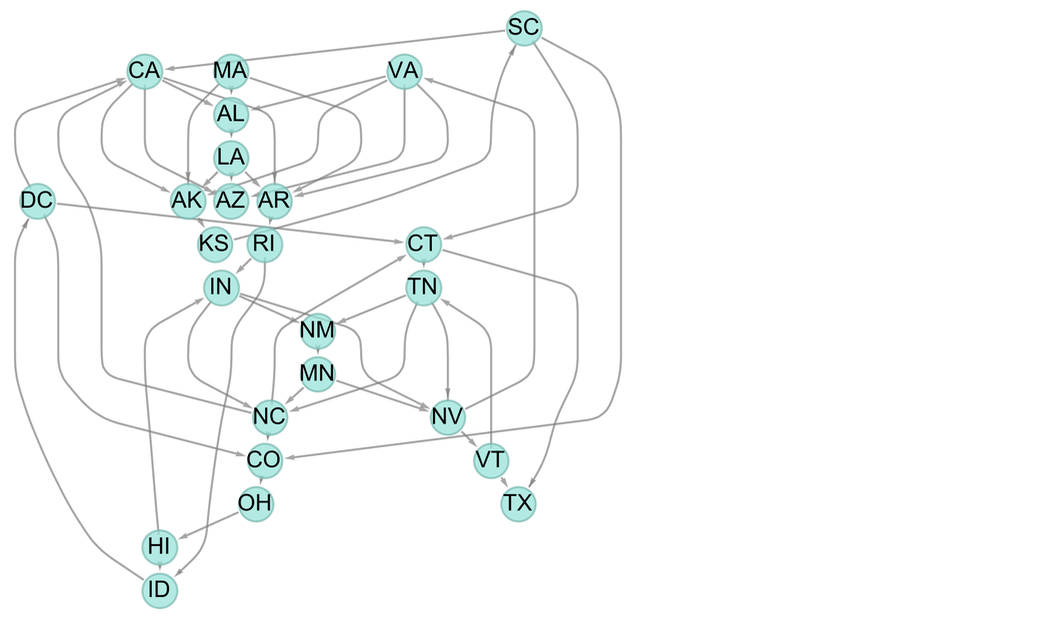
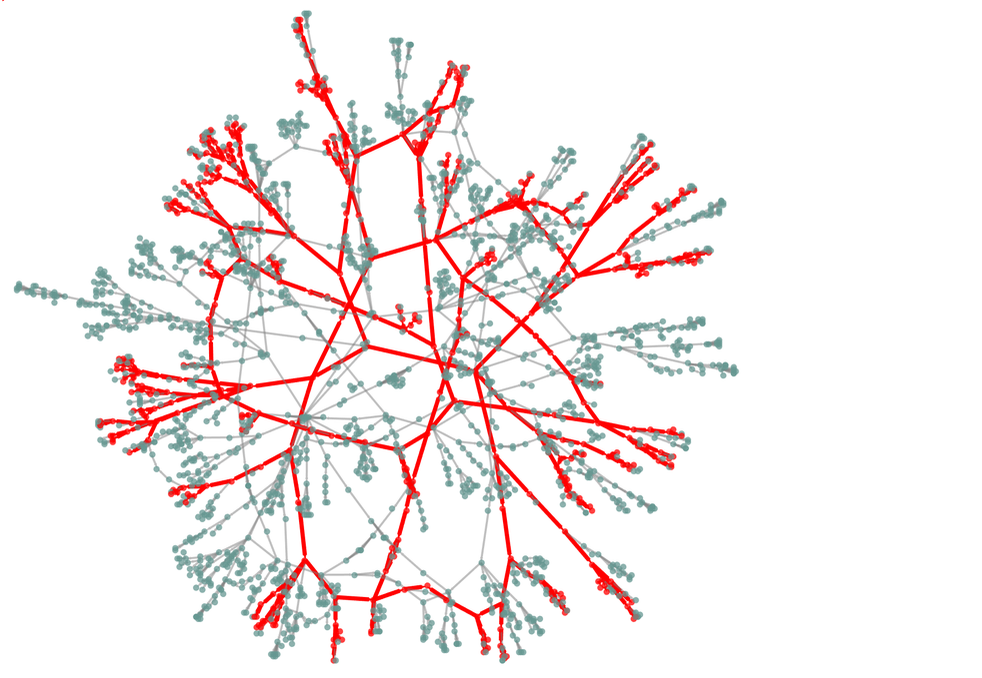
順便說一下,引向最長路徑的起始狀態是MN——它以2336種不同的方式達到長度24,可能的結尾是AZ、DE、KY和TX。幾個例子是:

在從MN開始的多路圖的前幾步中繪製這些路徑,我們得到:
群和(簡化的)魔方
Groups and (Simplified) Rubik’s Cubes
我們已經談論過那些本質上涉及圖結構上的行進(Walk)的謎題。一個特別著名的可以用這種方式思考的謎題的例子是魔方。有關的圖是由可應用於魔方的變換所形成的群(group)的凱萊圖(Cayley Graph)。
譯註:群(group)是一個數學術語,指一個集合和一個作用在這個集合的元素上的二元運算。這個集合需要滿足其中任意元素存在一個逆元素(inverse),以及存在一個單位元素(identity)。這個二元運算需要符合封閉性(運算結果仍然是集合中的元素)、結合律、單位元(在單位元素上應用該運算得到的仍然是單位元素)的性質。比如所有整數組成的集合和加法就構成一個群。凱萊圖(Cayley Graph)是群的結構一種可視化方法。(推薦 3B1B視頻 群論與808017424794512875886459904961710757005754368000000000)
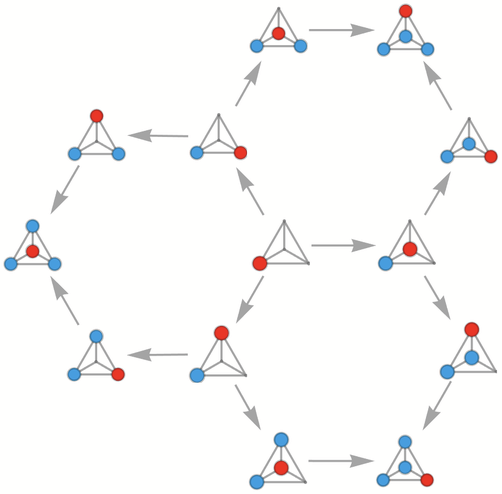
作為一個非常簡單的類比,我們可以考慮正方形的對稱變換群(the symmetry group of the square)(D4),基於鏡像反轉和90°旋轉的操作。我們生成的凱萊圖就像一個多向圖:通過在每一步應用每個操作。而在這個例子中,凱萊圖是:
譯註:藍色箭頭表示90°旋轉,綠色箭頭表示鏡像反轉
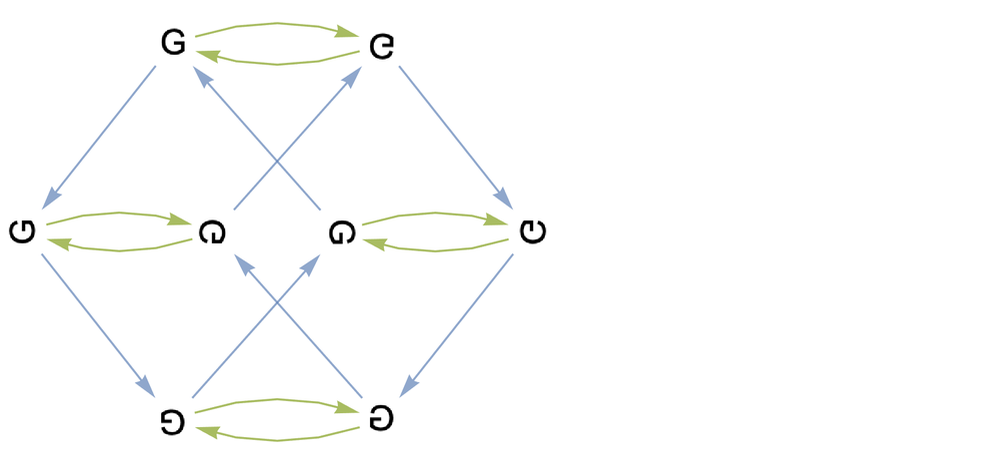
這個圖足夠小,可以直接看到如何從任何狀態到任何其他狀態。但是,儘管這個凱萊圖有8個節點,從任何一個節點到另一個節點的最大路徑長度為3,魔方的凱萊圖的節點數量卻有
最大最短路徑長度為20。
為了瞭解這樣一個事物的結構,我們可以考慮非常簡化的「2×2×2 立方體」的情況——只在其角上著色——每個面可以旋轉90°。

從上圖中的狀態開始,多路圖的第一步就是(注意,圖中的邊不是有向的,因為對應的轉換總是可逆的):
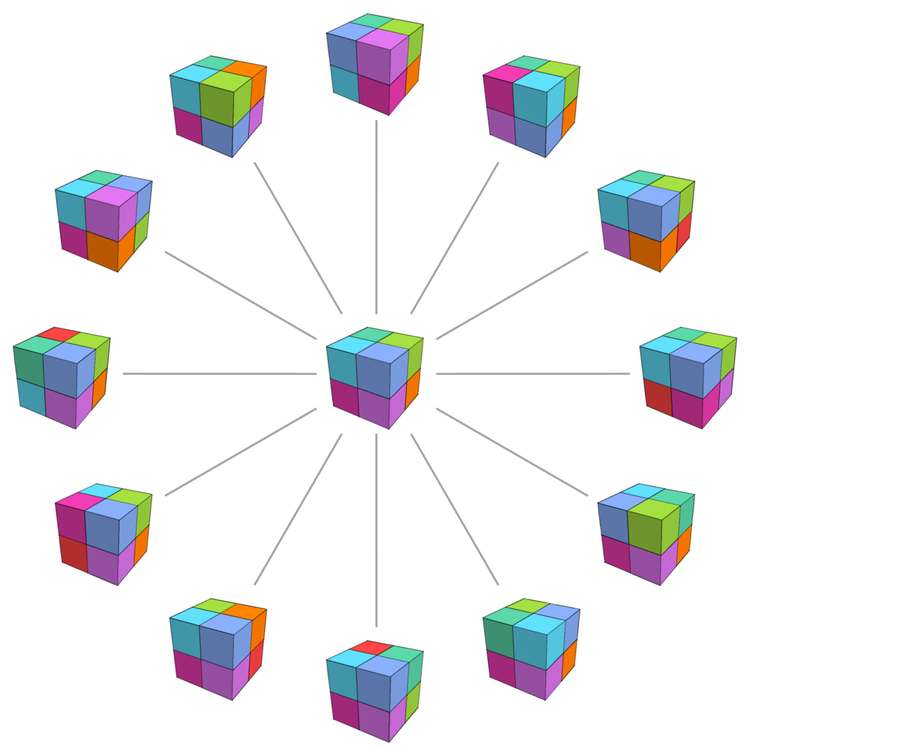
再多走一步就得到:
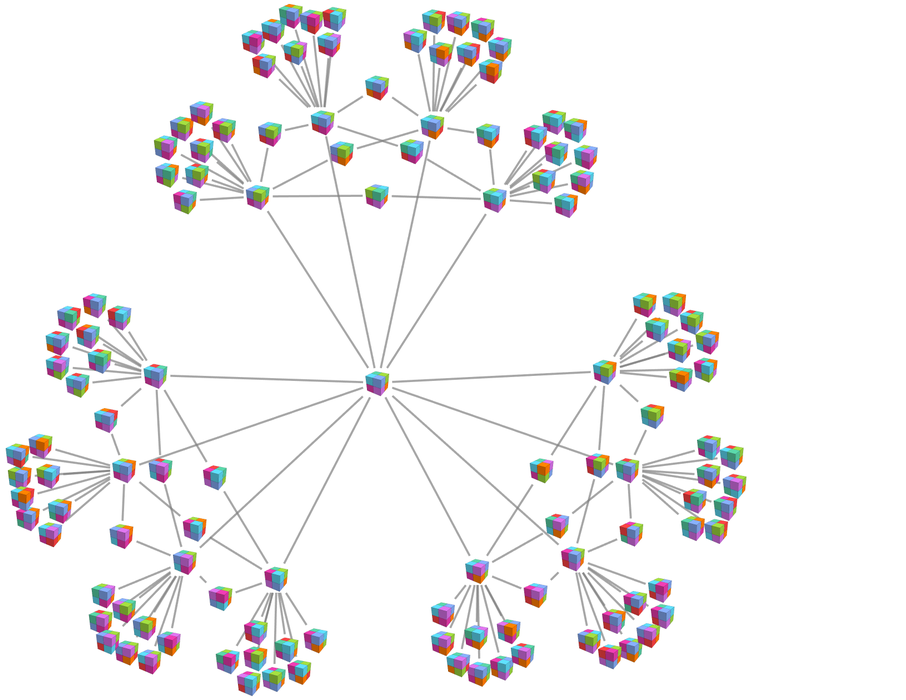
完整的多路圖(也是由變換產生的這個群的凱萊圖——就是S8)有8!=40320個節點(和483840條邊)。從一個狀態(即凱萊圖中的節點)開始,在連續的步驟中達到的新狀態的數量是:
圖中的最大最短路徑(maximum shortest paths)由8個步驟組成,一個例子是:

譯註:maximum shortest paths 指的是那些不是任何其他最短路徑的子路徑的最短路徑。比如假設 A-B-C 是A點到C點之間的最短路徑,A-B-C-D是A點到D點的最短路徑,那麼A-B-C就不是一個maxumum shortest path,因為另一條最短路徑A-B-C-D包含了A-B-C。
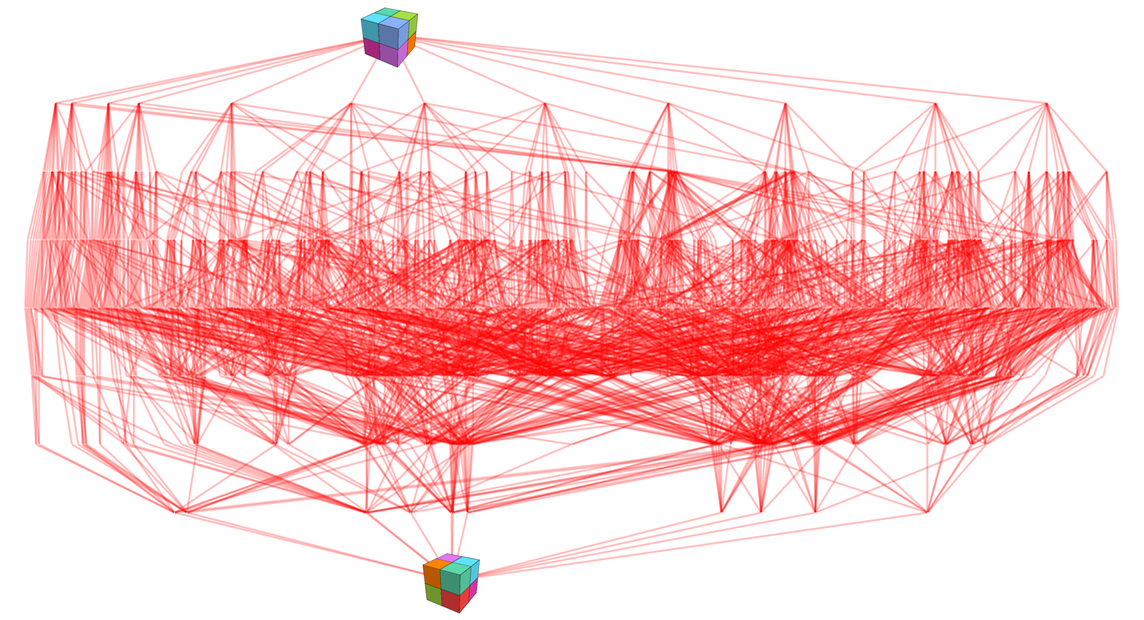
在這兩個特定的端點之間,實際上有3216條「測地(geodesic)」路徑——這些路徑在多路圖中分佈很廣。
譯註:「測地」路徑指球體結構上兩點之間的最短路徑。

只挑出測地路徑,我們看到有許多方法可以從立方體的一個狀態到達它的一個「反節點」(antipodes)。
孔明棋
Peg Solitaire
像井字棋這樣的謎題涉及到逐步填滿棋盤,而至少從16世紀開始使用的一大類謎題則涉及到從棋盤上移走棋子。典型的規則是棋子能夠跳過一箇中間的棋子進入一個洞,然後中間的棋子被移除。目標是最終在棋盤上只剩下一個棋子。
這裡有一個非常簡單的例子,基於一個棋子的T字形排列:

在這種情況下,只有一種方法可以「解開謎題」。
但在一般情況下,有一個多路圖:
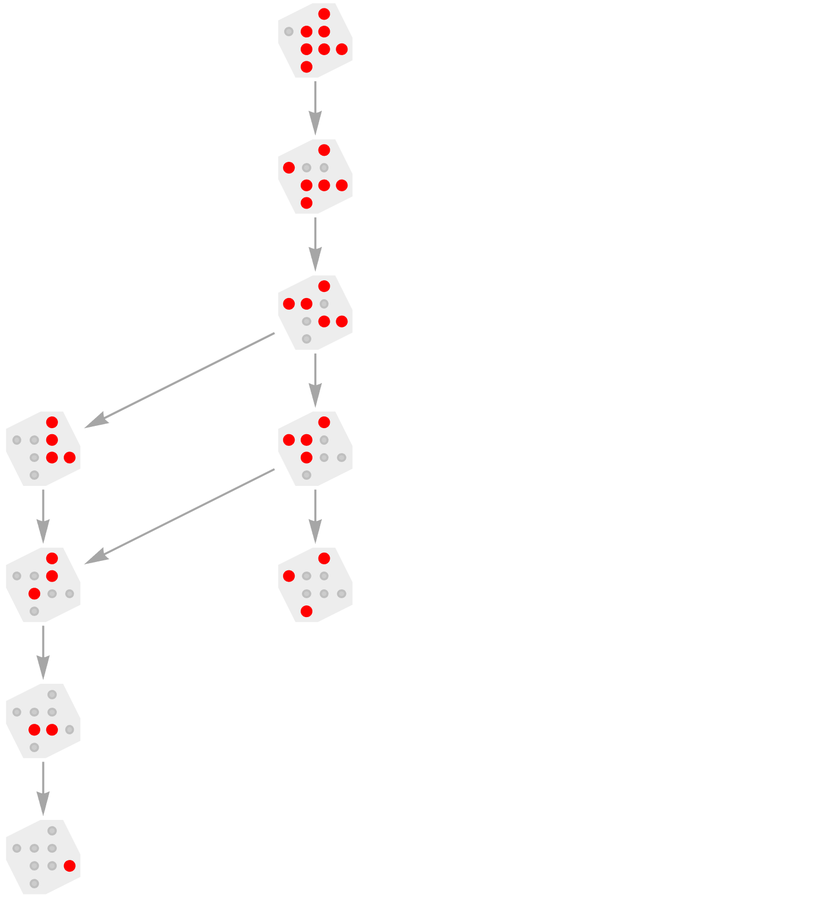
一個更復雜的例子是「棘手的三角形」(又稱「餅乾桶謎題(Cracker Barrel puzzle)」)。它的多路圖這樣開始:

再走幾步後,就變成了:
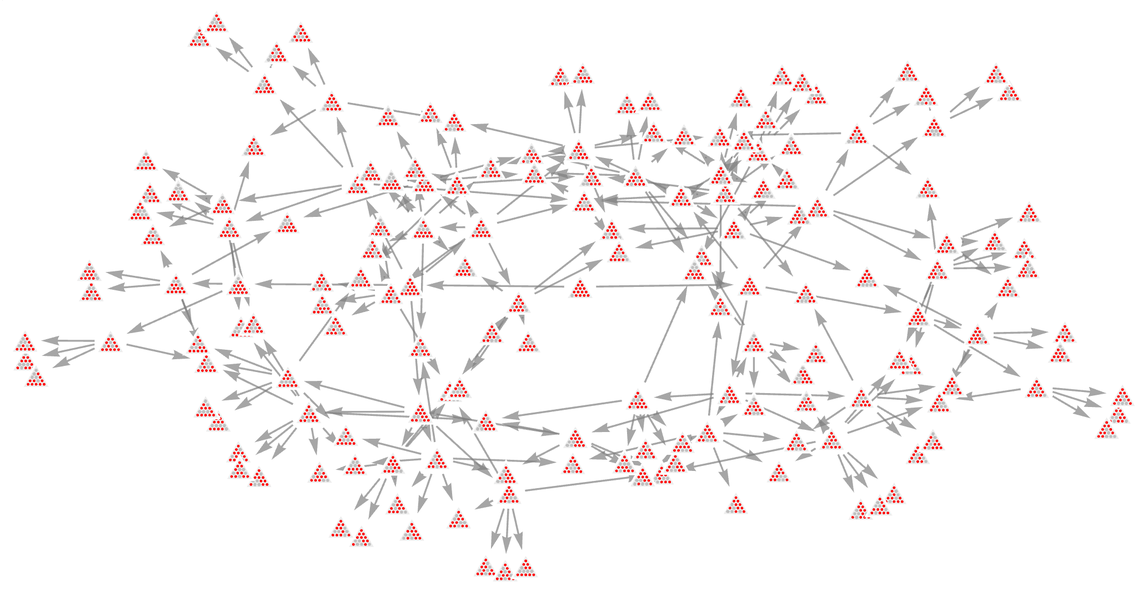
在最終的多路圖中總共有3016個狀態,其中118個是「死衚衕」,從那裡不可能有進一步的行動。這些死衚衕狀態中「最早能達到」的是:

可以達到的「獲勝狀態」只有4個,而導致這些狀態的「終局」是:
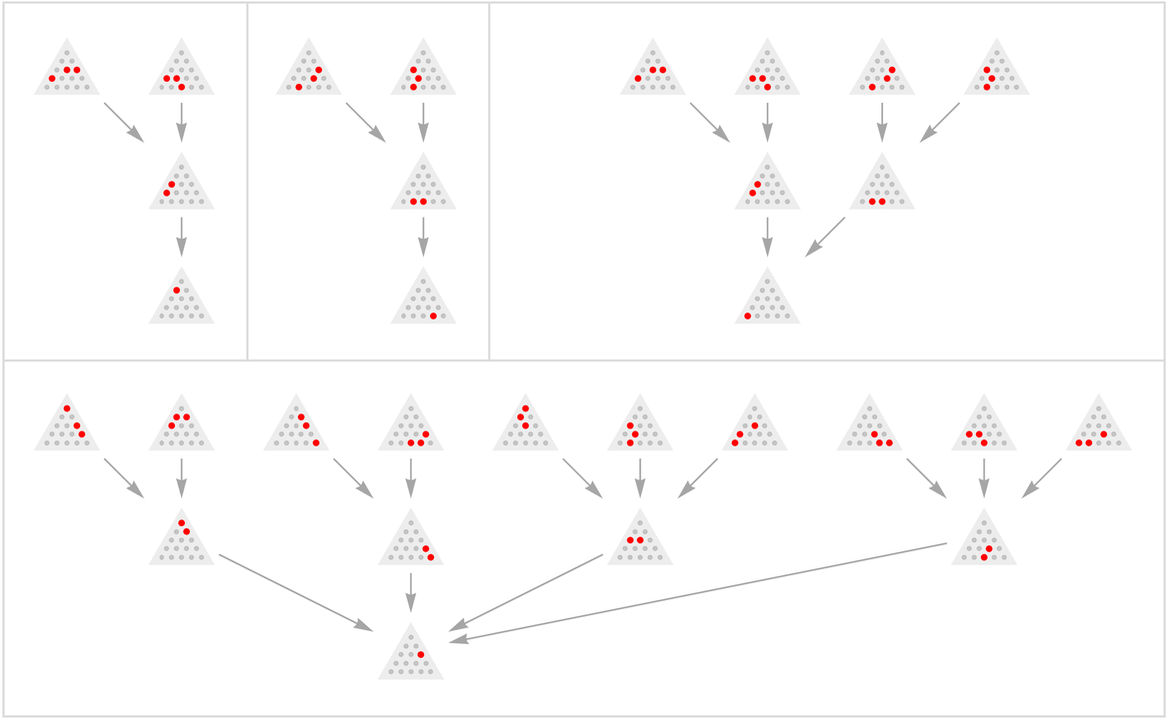
從初始狀態開始,每一步達到的可能狀態的數量如下,其中可以導致獲勝的狀態顯示為黃色:
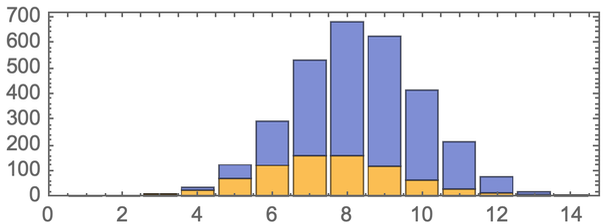
下圖展示了完整的多路圖,並高亮顯示了「獲勝路徑」:
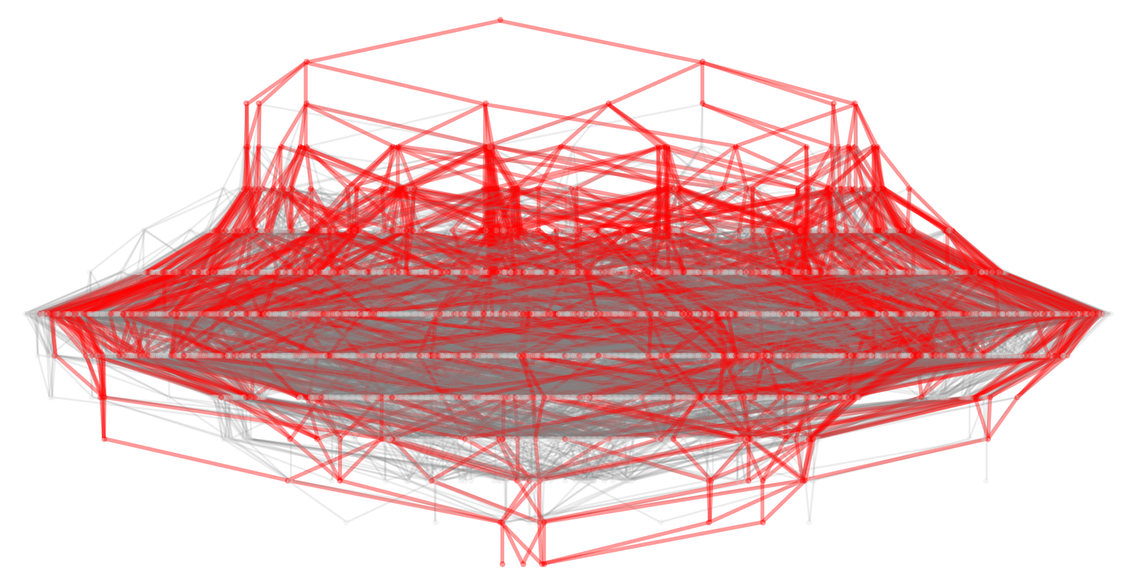
在連續的步驟中,能夠導致獲勝狀態的狀態的比例如下:
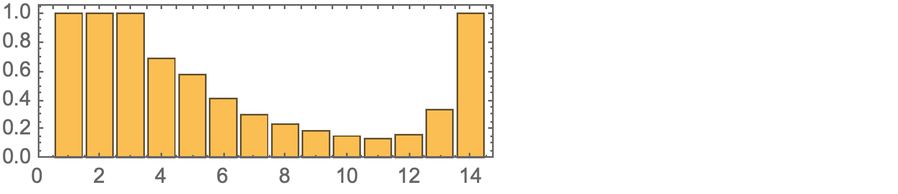
分支圖是高度連接的,這意味著在某種意義上,這個謎題直到最後仍然是「均勻混合的(well mixed)」和「不可預知的」:

西洋跳棋
Checkers
孔明棋是一種單人「遊戲」。西洋跳棋是一種雙人遊戲,規則有點類似。
「黑」棋和「紅」棋在棋盤上向不同方向斜向移動,當它們相鄰時,通過跳過對方棋子來「吃掉 」對方的棋子。
考慮一個相當小的4×4棋盤的例子。
「黑」和「紅」的基本走法由下圖(注意,4×4棋盤太小,不支持「多跳」):

我們可以立即開始生成一個這個情況下的多路圖,基於黑棋和紅棋的交替進行:
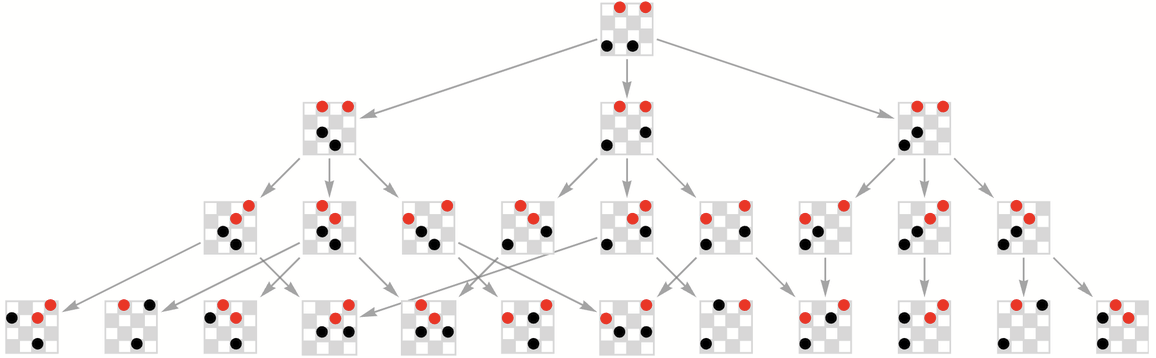
按照目前定義的規則,完整的161個節點的多路圖是:

在這種簡單的4×4情況下,「贏」的含義並不完全清楚。但可以說,當對方在下一步棋中不能做任何事情時就贏了。這與多路圖中的「死路(dead ends)」相對應。這種情況有26個,其中只有3個發生在紅方下一步棋的時候,其餘的都發生在黑方的時候:

如前所述,任何特定的遊戲過程都對應於多路圖中從根狀態(root state)到某個終止狀態的路徑。如果我們看一下這種情況下的分支圖,我們會發現它們有許多不相連的子圖,這表明對於這個簡單的遊戲來說,有許多基本獨立的「遊戲路徑」——所以沒有多少結果的「混合」。
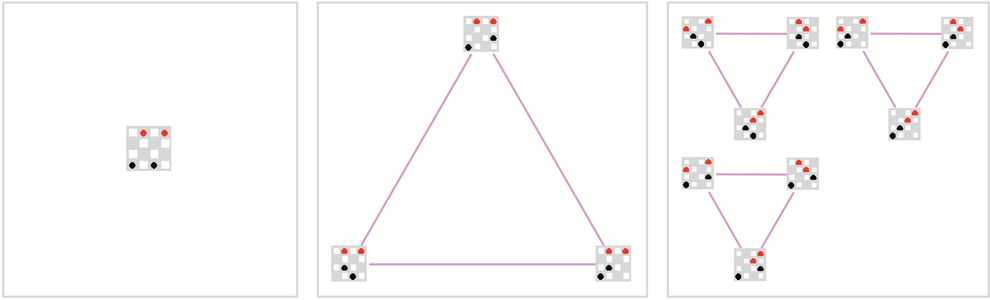
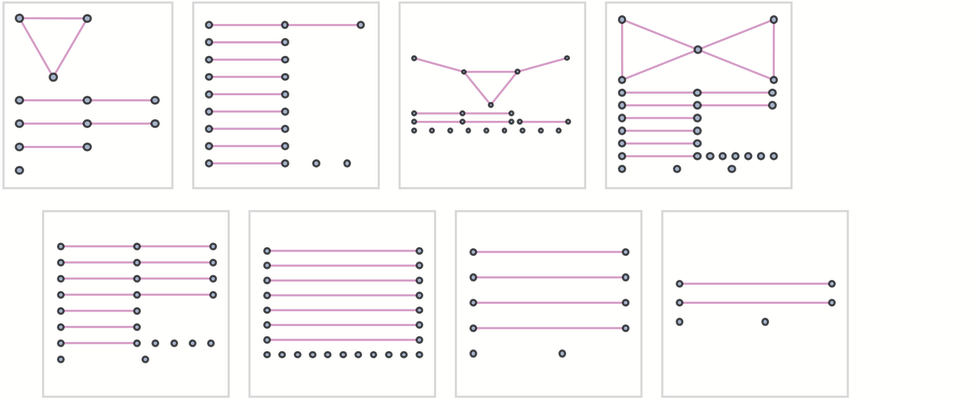
到目前為止,我們使用的規則沒有考慮到跳棋的第二層規則:當一個棋子到達棋盤的另一邊時,它就成為一個「國王」,允許向後和向前移動。即使只有一個棋子和一個棋手,這也已經產生了一個多路圖——尤其現在圖中有了循環:
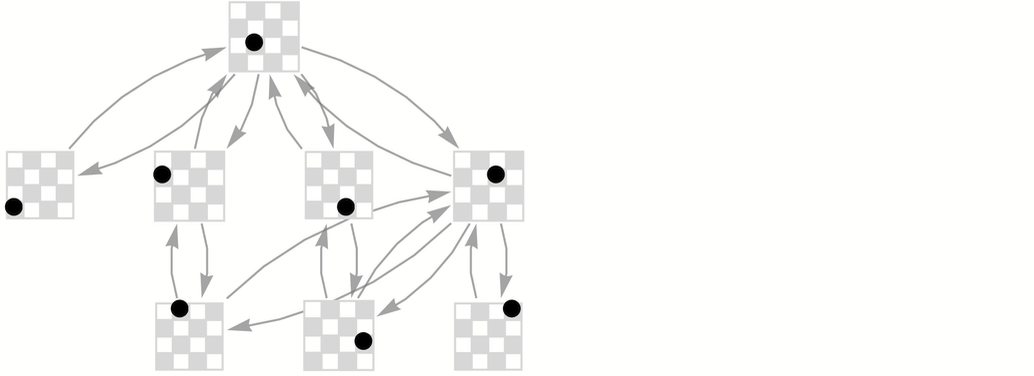
或者換一種佈局(有明確的無向邊):
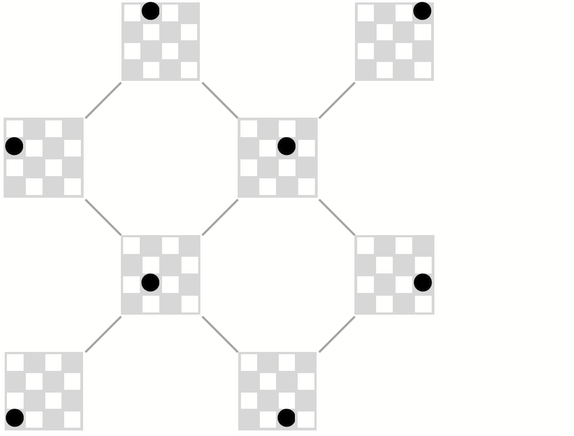
有了兩顆棋子(兩個玩家輪流),「國王」多路圖是這樣開始的:
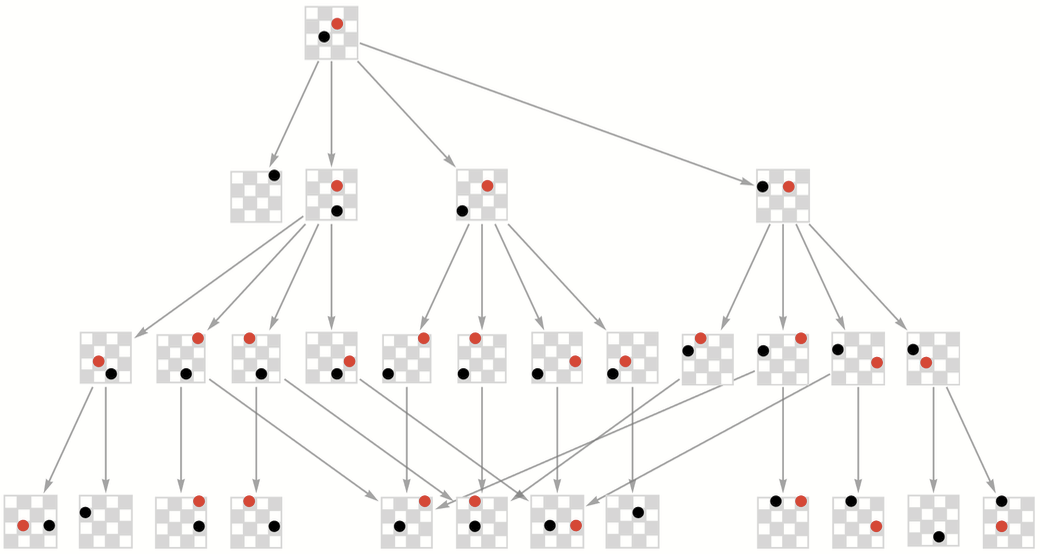
在這個初始棋局下,但不考慮後退的動作,整個多路圖就可以簡化為:

完整的「國王」多路圖在上述條件下也只有62個節點——但包括各種循環(儘管有這麼少的棋子並且讓黑棋先下,且任何勝利都不可避免地會是黑棋的):

在我們最初的初始條件下的普通+國王的多路圖又如何呢?組合圖有161個節點來自「前國王」階段,4302個來自「後國王」階段——下圖給出了最終形式:

(極其簡化的)圍棋
(Very Simplified Go
完整的圍棋遊戲是錯綜複雜的,在任何現實情況下,它的多路圖都太大了,我們根本無法明確地生成(儘管人們當然可以想一想是否有有意義的「連續極限(continuum limit)」結果)。然而,為了能對圍棋有點概念,我們可以考慮一個非常簡化的版本,在這個版本中,黑色和白色的 「棋子」被逐步放在圖的節點上,如果一方成功地包圍了連成一片的另一方的棋子,遊戲就被視作「勝利」。
想象一下,我們從一個由2×2網格組成的空白「棋盤」開始,然後在一連串的「回合」中以所有可能的方式添加黑白棋子。由此產生的多路圖是:

每一個在這裡沒有後繼情形的狀態都是黑或白方的勝利。
「黑勝」(高亮顯示了被包圍的棋子)是:

而「白勝」則有:

在這個層面上,我們所擁有的基本上相當於2×2的井字棋——除了後者有一個「對角線」的勝利條件。
在一個3×2的「棋盤」上,多路圖的前兩步是:

完整的多路圖是:
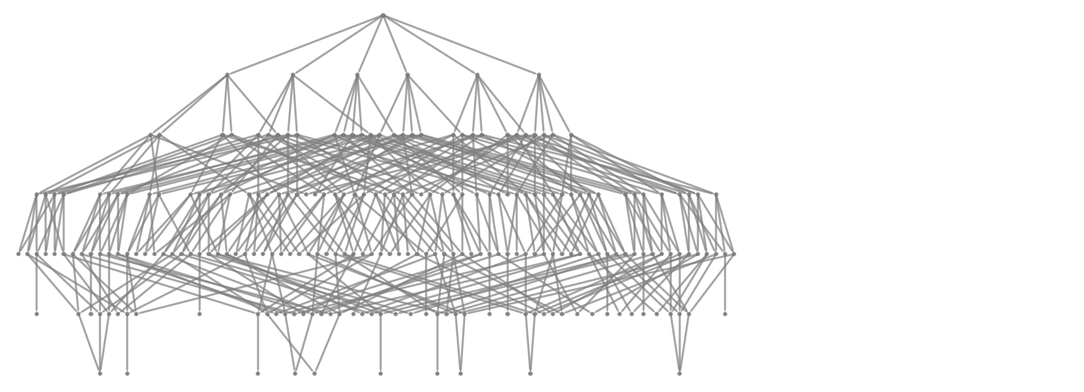
該圖有235個節點,其中24個是白方的勝利,34個是黑方的勝利:
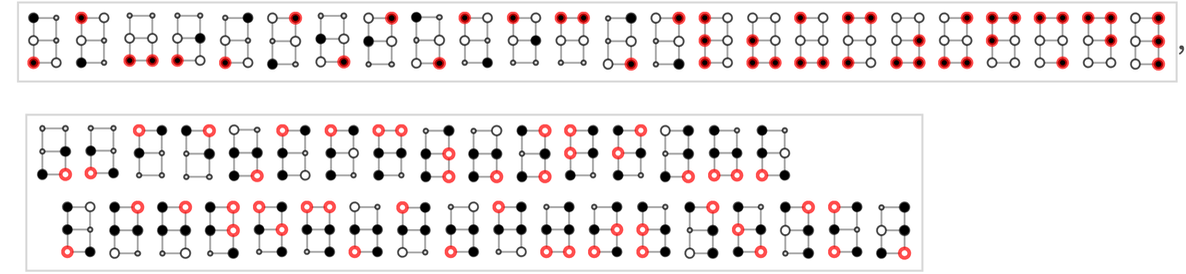
在這種情況下,連續的分支圖是(圖中標明瞭是哪方勝利):
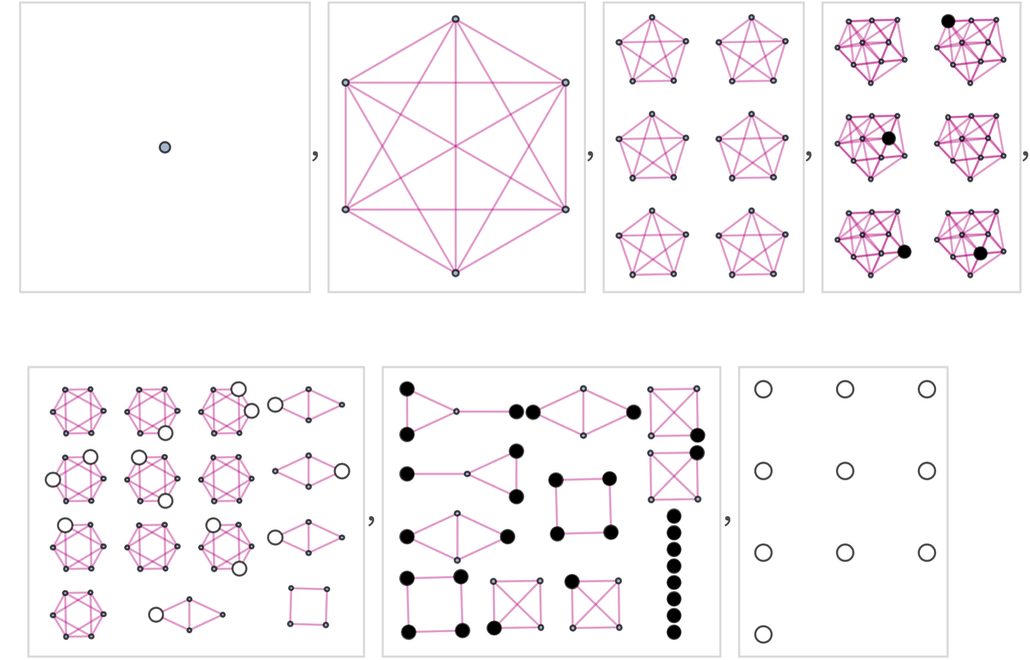
對於一個3×3的「棋盤」來說,多路圖有5172個狀態,其中604個是白方的勝利,684個是黑方的勝利。
尼姆遊戲
Nim
作為另一個簡單遊戲的例子,我們現在考慮尼姆遊戲(Nim)。
在尼姆遊戲中,有k堆物體,每一步中,p個玩家交替從他們選擇的任何一個物體堆中去除任意數量的物體。遊戲的失敗者是被迫處在所有堆中都沒有物體的玩家。
從兩堆各含2個物體開始,我們可以為這個遊戲構建一個多路圖:
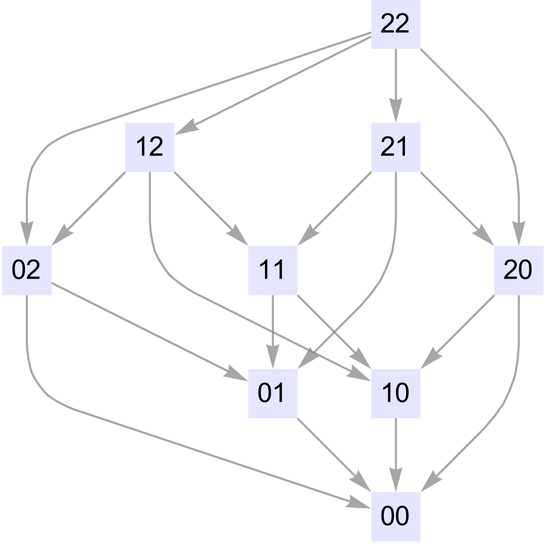
如果有三堆的物體,這個多路圖就變成了:
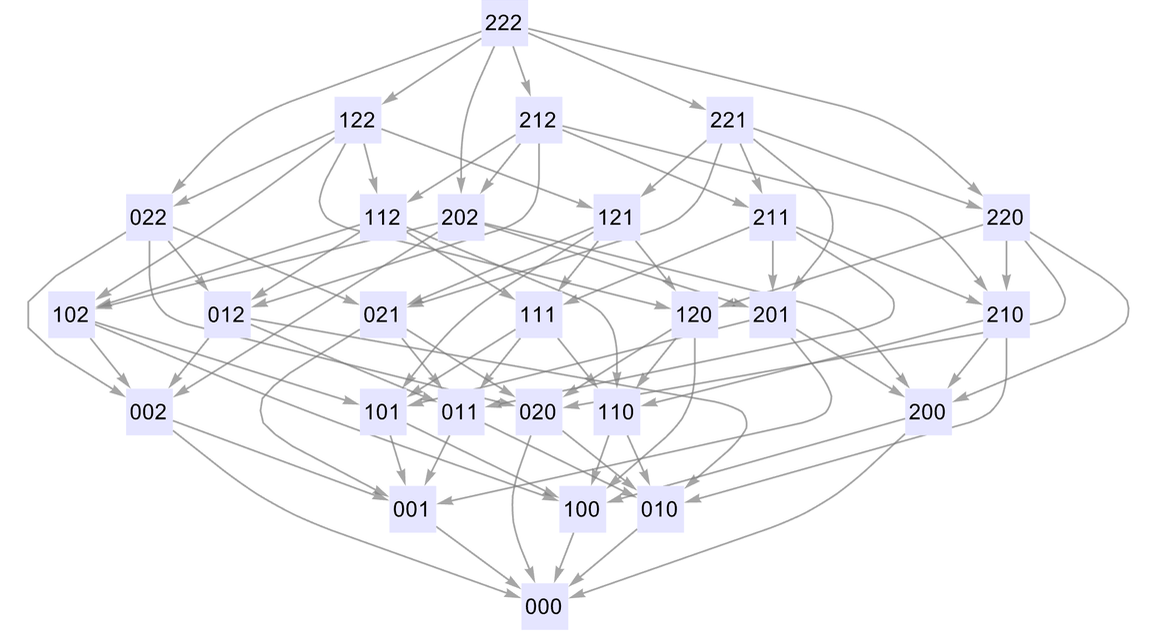
這些圖顯示了將物體堆的不同狀態相聯繫的所有不同的可能棋步。然而,它們並沒有指出哪位棋手在什麼時候移動。加上這點,我們在2-2情況下得到:

而在三個物體堆、每堆有2個物體(2-2-2)的情況下:
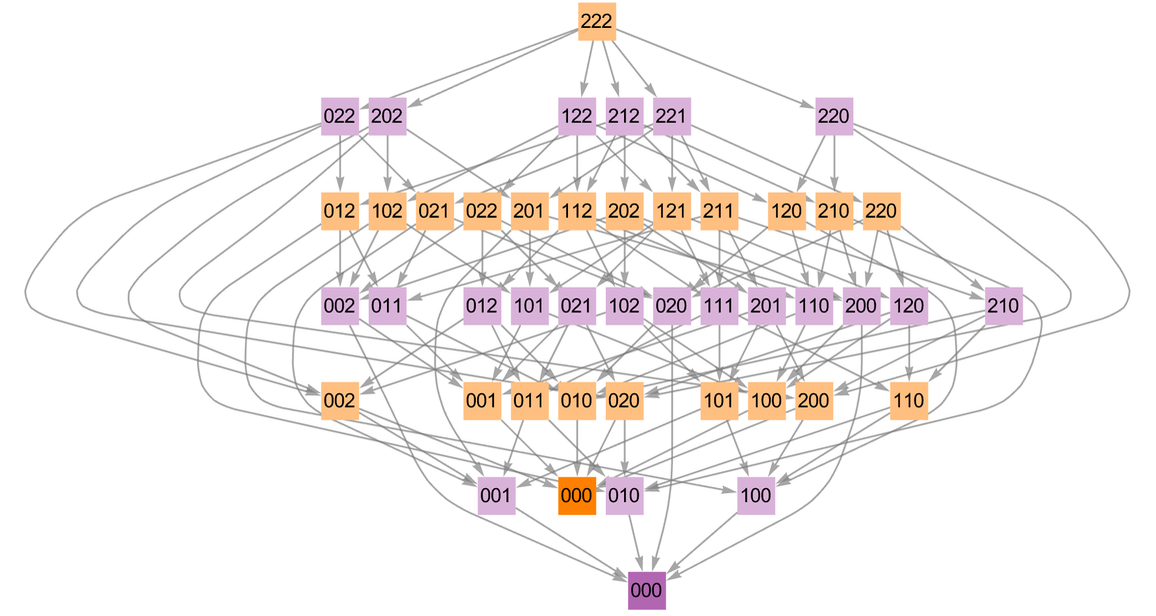
儘管這些圖看起來有些複雜,但事實證明,對於一個特定的狀態何時具有可以保證「對手」輸掉的屬性,有一個非常直接的標準:只要拿著數字列表,看看這個列表中的數字按比特位取異或(bitwise XOR )之後是否為0。
譯註:按比特位取異或指將兩個數字轉換成二進制之後,比較每一個位是否相同,同為0,異為1,最後得到另一個二進制數。結果可以再與第三個數進行異或操作(同為0,異為1),以1此類推。比如 BitXor[2,2,2] = 11 ^ 11 ^ 11 = 00 ^ 11 = 11 = 2,其中粗體表示二進制數。
標記這些狀態,我們得到(譯註:下圖中用深紅色做標記):

在三個物體堆、每堆有2個物體(2-2-2)的情況下,這個分支圖序列變成了:

下圖展示了一些其他情況:
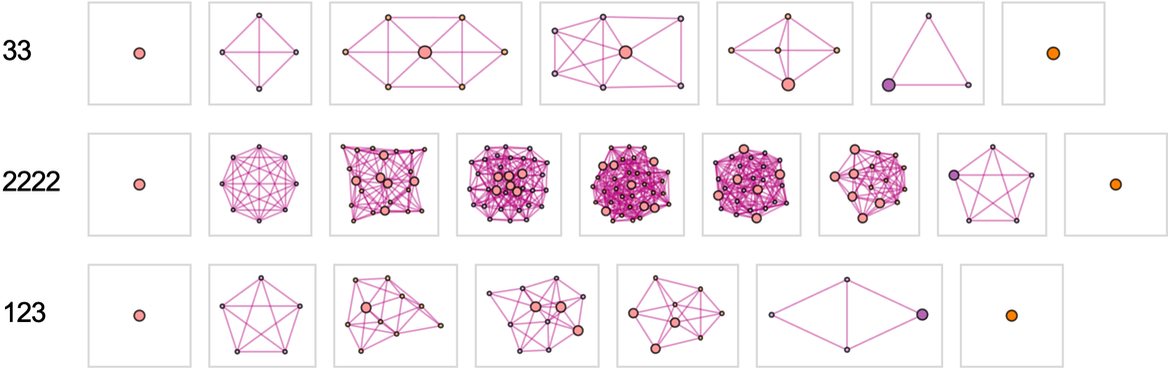
滑塊謎題
Sliding Block Puzzles
這類遊戲有很多名字,有很多不同的主題。
但許多謎題本質上都是滑塊謎題。
一個簡單的例子可能是要求從下面的左圖變換成右圖:

變換是通過將積木滑入空(較暗)的方塊完成的。
這個謎題的一個解是:

可以用一個多路圖來表示所有可能的變換:
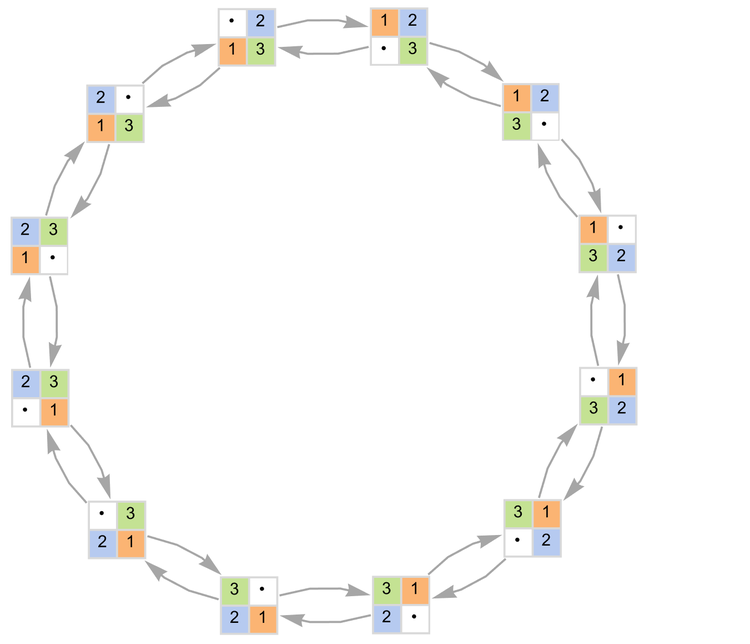
(注意這4!= 24個可能的狀態中只有12個出現在了上圖中;像下面這樣的狀態

是不可能達到的。)
由於滑塊總是可以「雙向滑動」,所以滑動積木謎題的多路圖中的每條邊都有一個逆向(inverse),因此,我們就把這些多路圖畫成無向圖。
下面是幾種簡單的情況:
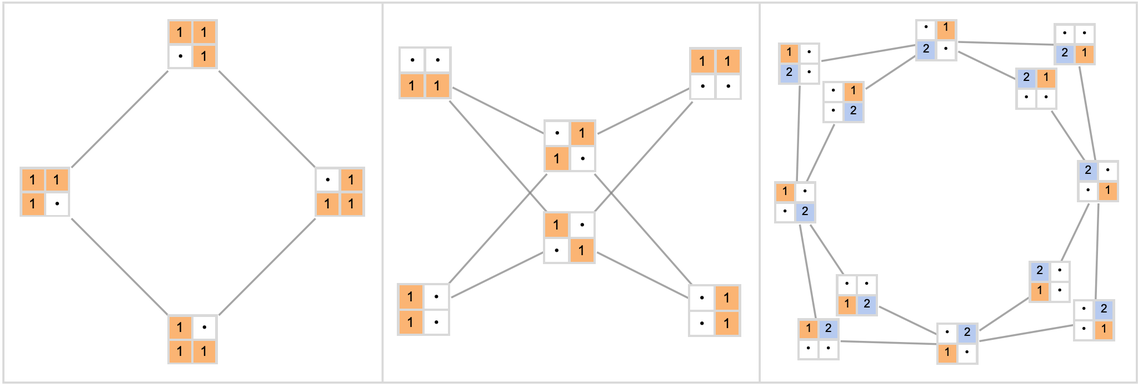
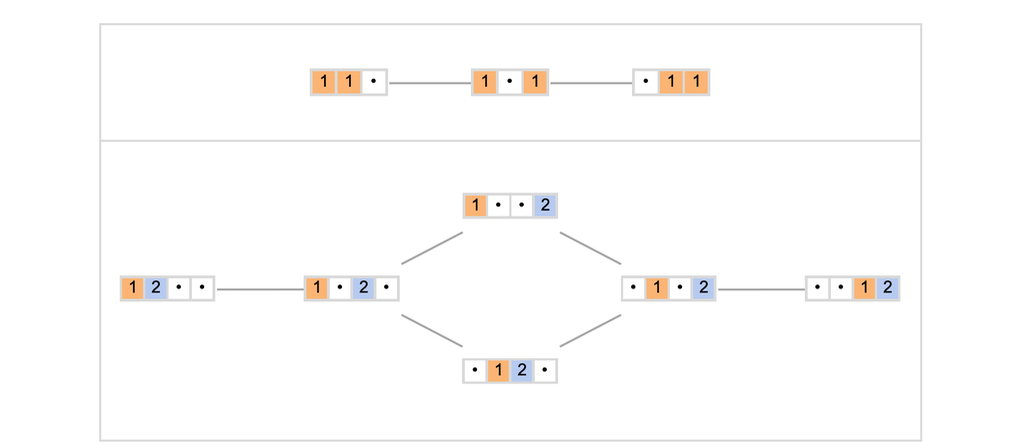
當我們考慮3x2規模的網格時,情況一下子就複雜起來了:
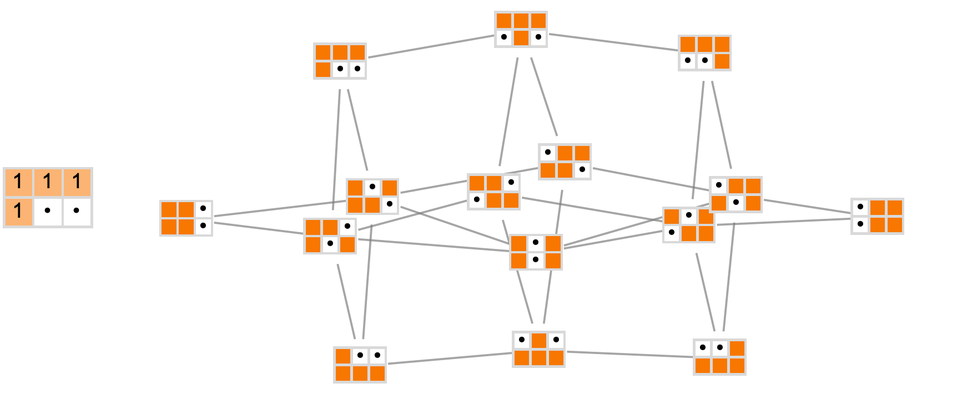
在3維的表示下這個多路圖是:

當所有的積木都不同的時候,人們傾向於得到具有某種球形結構的多路圖:
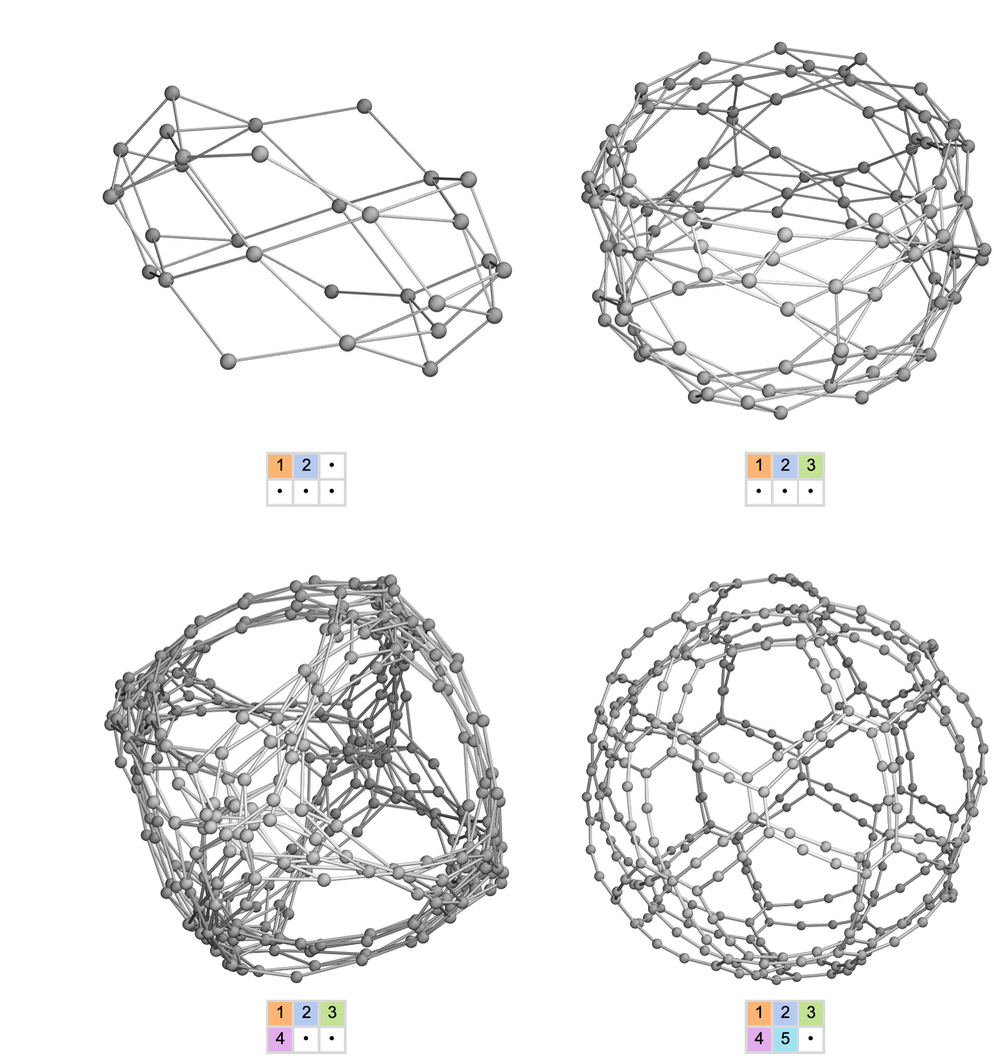
(請注意,在前三種情況下,有可能達到所有30、120、360個可想象的積木排列,而在最後一種情況下,只能達到積木的「偶數排列」,或720個可想象的排列中的360個)。
以及這張圖的標記部分展示了從

到達

的路線:
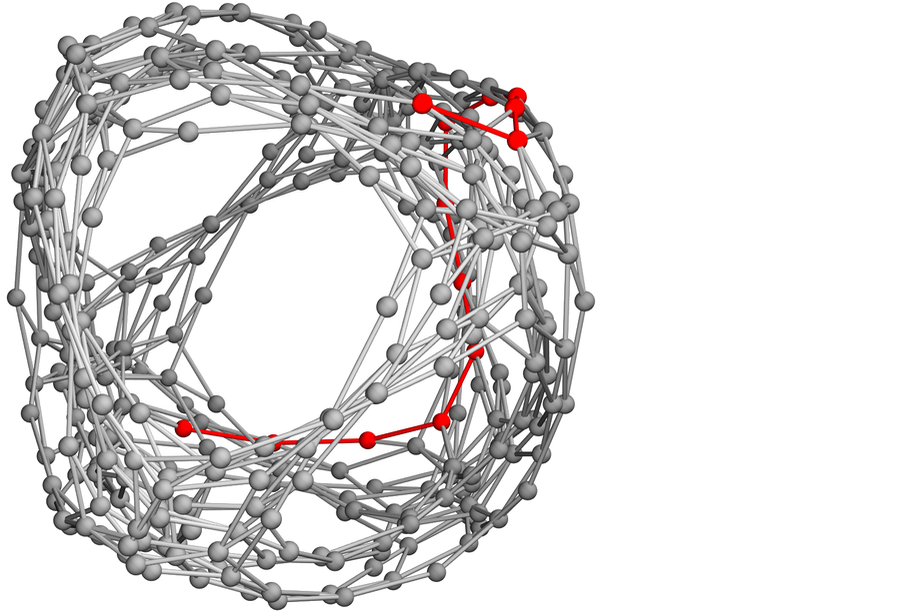
如果有許多相同的積木,通常會形成簡單的網格狀結構:

而如果只是讓一個積木不同,基本上只是在這個網格圖中「增加裝飾」:

隨著「1」和「2」的積木的數量越來越接近於相等,結構就會被填滿:
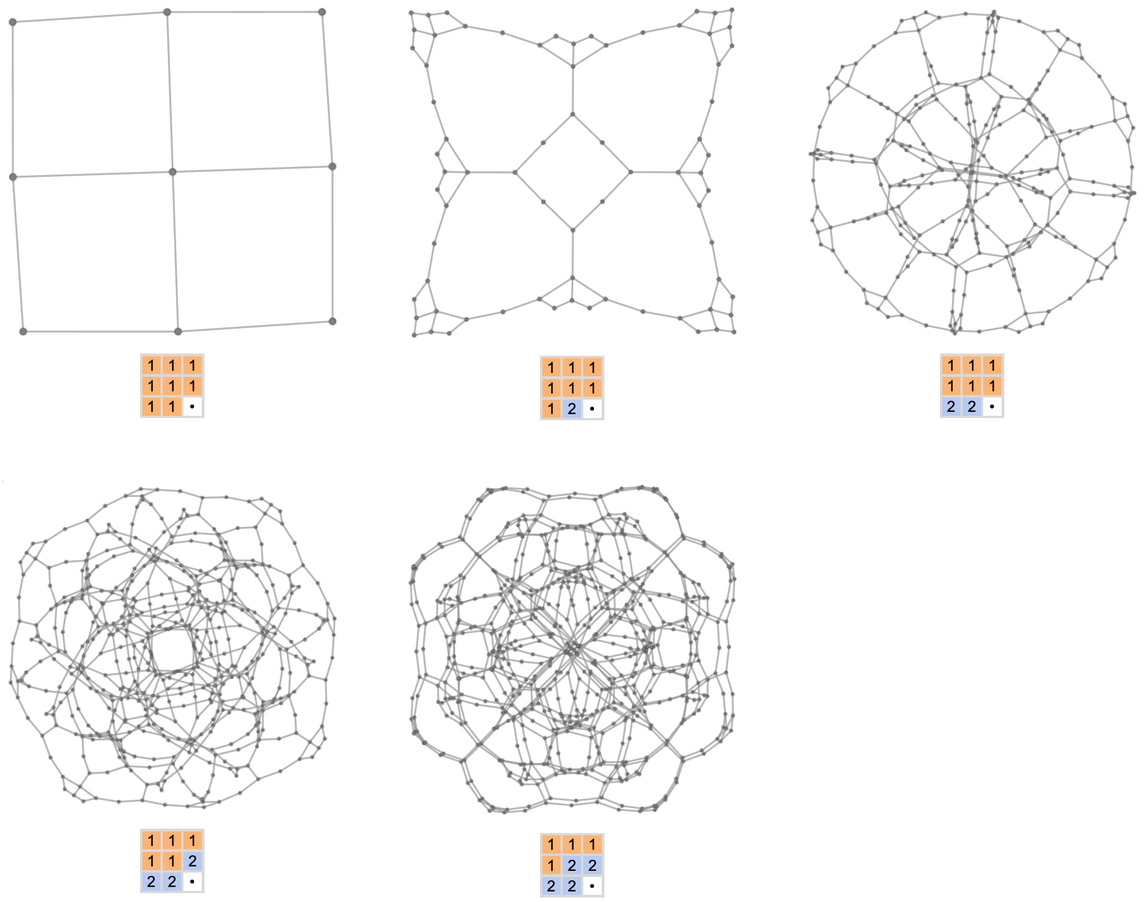
添加第三種類型的積木會迅速導致一個非常複雜的結構:

下圖總結了一些多路圖的情況:
漢諾塔,等等
Towers of Hanoi, etc.
另一個著名的謎題是漢諾塔(Towers of Hanoi)。
我們可以為它也構建一個多路圖。從左邊的所有盤子開始,多路圖的第一步是:
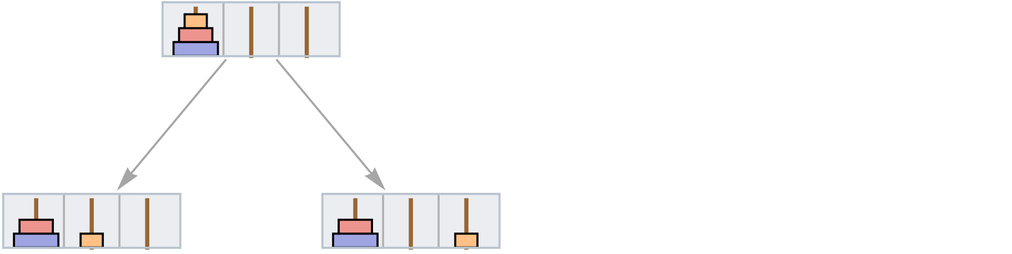
前進兩步就得到:

從而完整的多路圖就是(展示的是無向邊,以代替成對的有向邊):
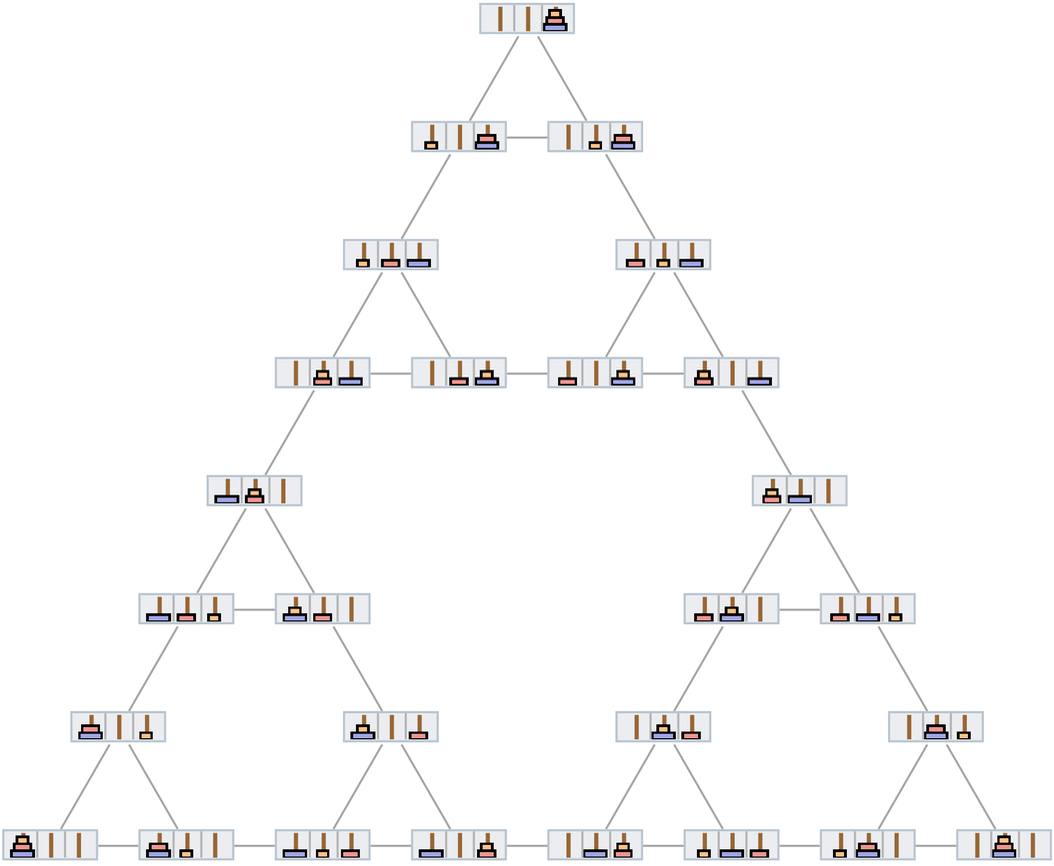
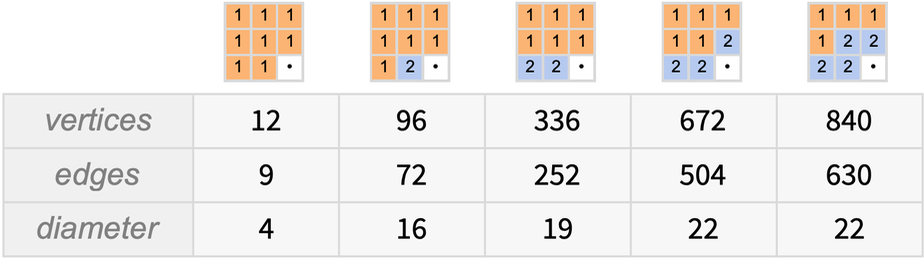
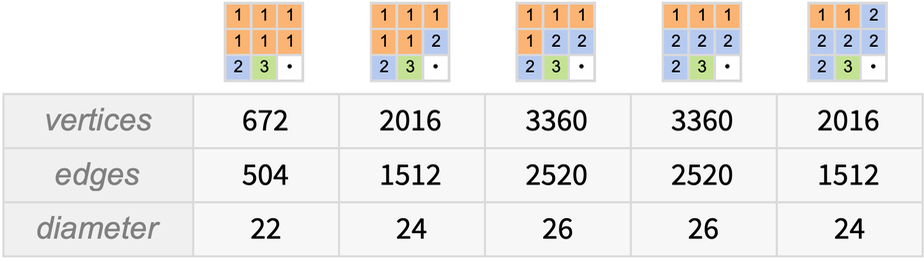
很容易看出這個多路圖的遞歸結構是如何建立起來的。
下圖是2個圓盤(和3根柱子)的「基礎情形」:
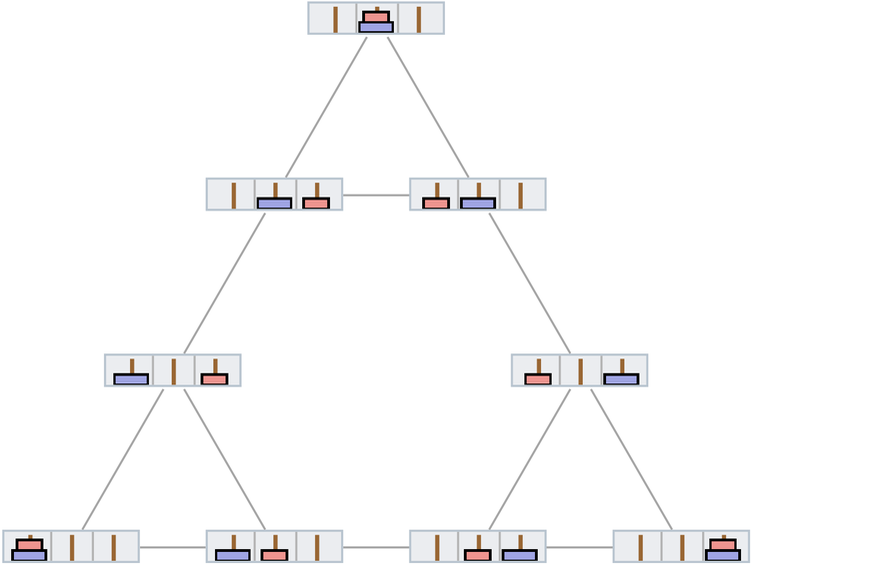
每增加一個圓盤,多路圖中的節點數量就增加3倍,例如,有4個圓盤(仍有3根柱子)。

如果有4根柱子,事情起初看起來更復雜,即使只有兩個圓盤:
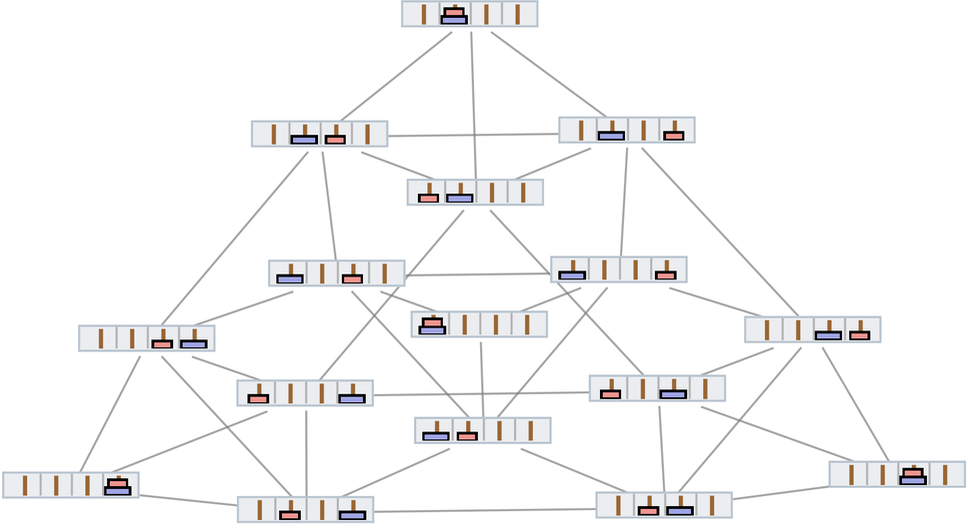
在三維的可視化下能看出更明顯的結構:

下面分別是3個、4個和5個圓盤的結果——「耳朵上的點」對應於所有圓盤都在一個柱子上的狀態。

在3根柱子的情況下,最短步驟數的「謎題解決方案」——將所有圓盤從一根柱子移動到另一根柱子——沿著多路圖的「邊」走,對於n根柱子來說,長度為2n - 1:
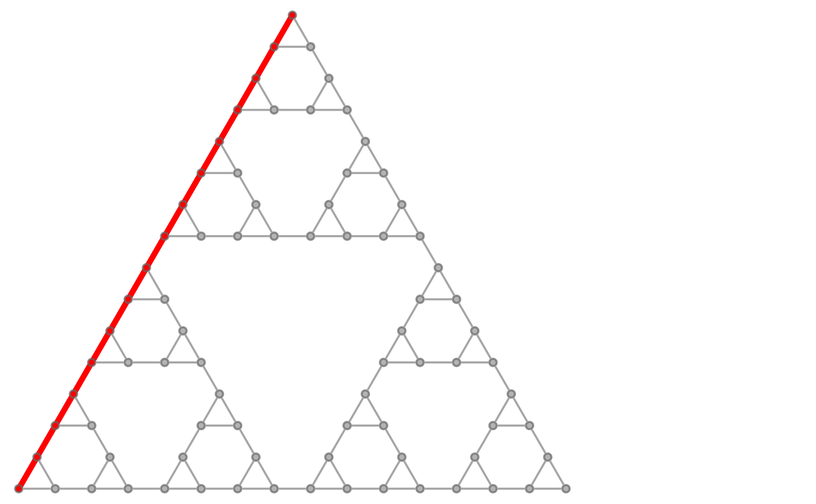
4根柱子的情況下,就不再有唯一的「測地路徑(geodesic path)」了。
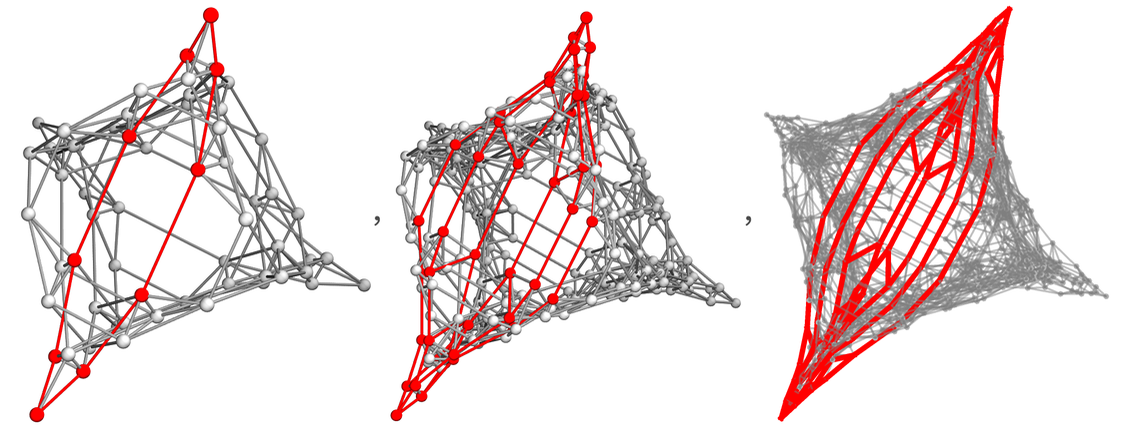
(並且連續的柱子數量下路徑長度組成的序列是

或者對於很大的柱子數量n來說,路徑長度略低於
那麼分支圖呢?
對於標準的3個圓盤和3根柱子的情況,我們有:
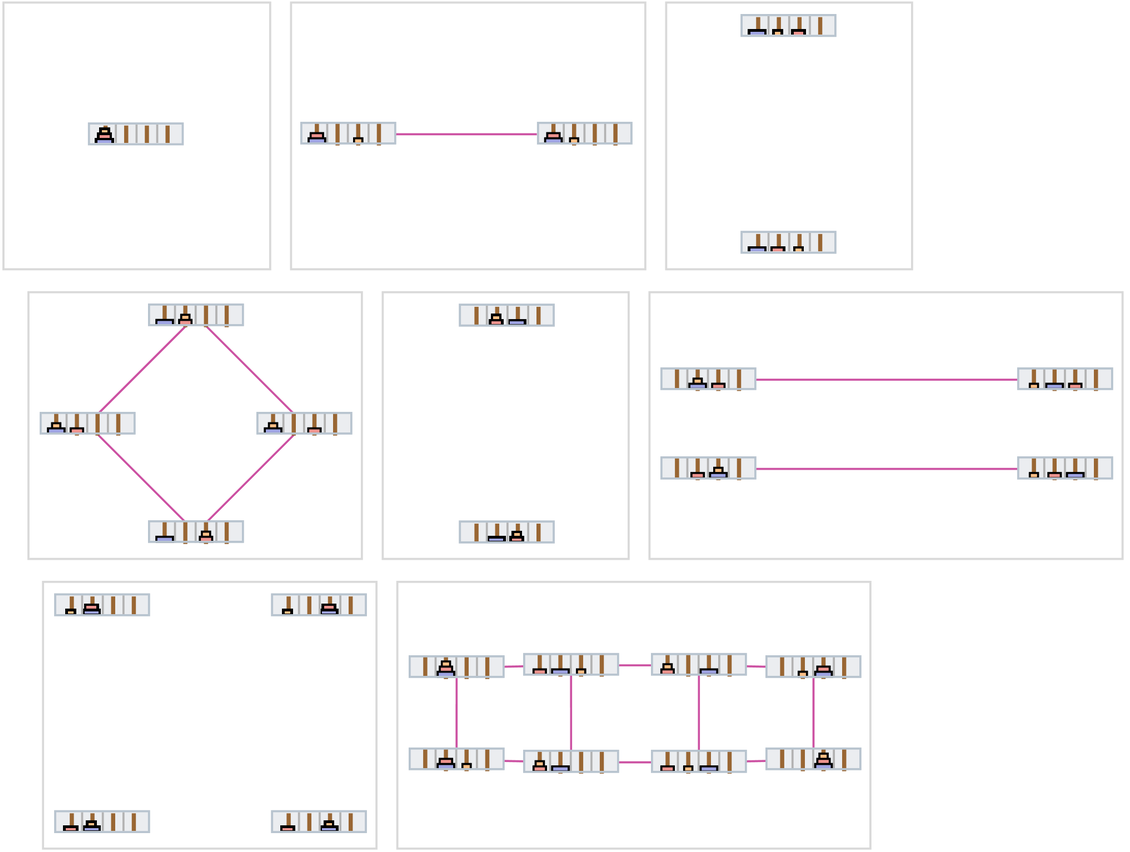
其中,連續的「時間切片(time slices)」被認為是通過觀察上述多路圖的連續垂直層次而獲得的。
對於4個圓盤的情況,我們實質上得到的「基本上是同樣的東西」:
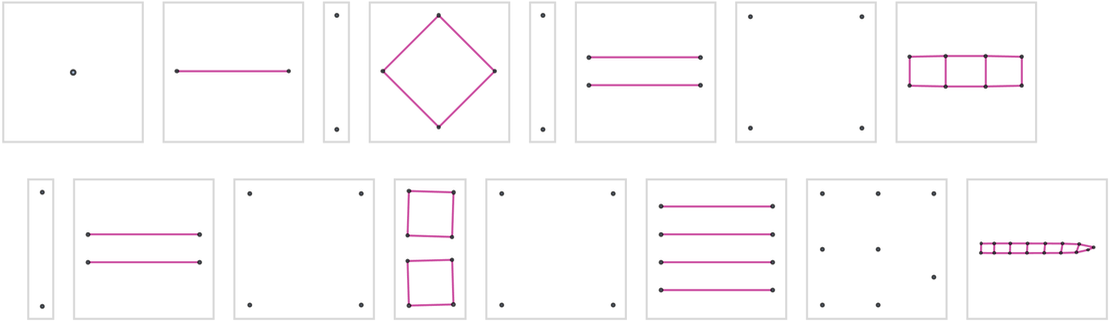
而4根柱子就讓問題變得稍微複雜了:
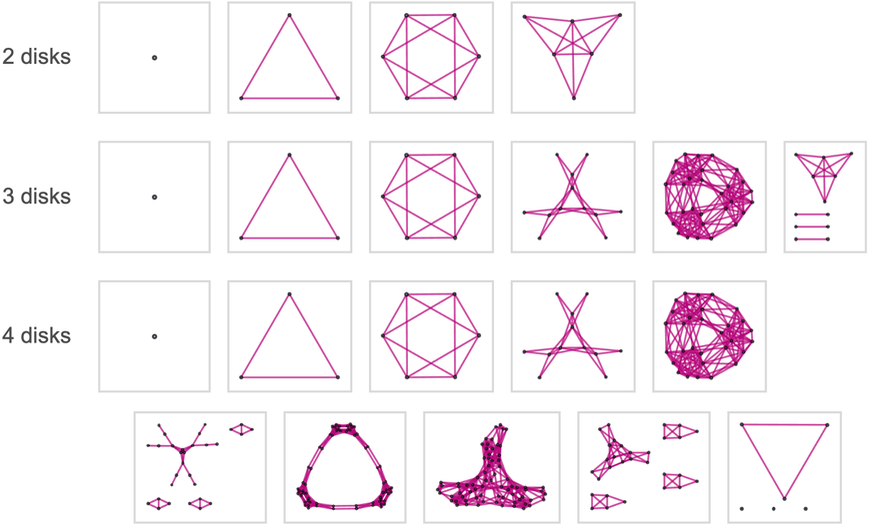
5根柱子的情況也延續了這個趨勢:

多重計算視角下的推論和闡釋
Multicomputational Implications & Interpretation
我們已經考察了許多遊戲和謎題的例子。在每一個例子中,我們都探索了囊括了整個可能行為譜系的多路圖。那麼,我們的結論是什麼呢?
最明顯的一點是,如果遊戲和謎題在我們看來是困難的——或者說是「有趣的」——它在某種程度上為多路圖的顯著複雜性所反映。或者,換句話說,當我們發現多路圖在某種程度上「難以解碼(decode)」時,我們就會得到一個豐富的、吸引人的遊戲或謎題。
在玩一個遊戲的任何特定實例中,我們基本上是沿著一條特定的路徑(與物理學相類似,我們可以稱之為「時間路徑(timelike path)」)穿過遊戲的多路圖(或「遊戲圖」)。並且在某種程度上,我們可能只是做了一個全局性的聲明,即遊戲圖代表了所有這樣的路徑。
但多重計算範式(Multicomputational paradigm)所建議的是,我們還可以有效地做出更多的局部聲明。特別是,在沿著一條時間路徑的每一步,我們可以在多路圖中「橫斷地(transversally)」觀察,並看到「瞬時分支圖」,它代表了我們的路徑與「鄰近路徑」的「糾纏(entanglement)」。
從而,某種意義上說,弄清「下一步該做什麼」就是決定在分支空間中「朝什麼方向」走。而遊戲的困難之處在於,我們無法輕易預知我們「穿越分支空間」時發生了什麼。這裡有一個與計算的不可還原性(computational Irreducibility)概念的某種類比。沿著一些時間路徑從一個狀態到另一個狀態,計算的不可還原性意味著,即使我們可能知道根本的規則,我們也不能輕易地預測其結果——因為這可能需要不可減少的計算量來計算出許多步驟之後的結果。
預測「穿越分支空間」是一個相關的、但稍有不同的現象,人們可以將其描述為「多重計算的不可還原性(multicomputational irreducibility)」。這不是關於計算出一個特定路徑的困難,而是關於看到許多糾纏的路徑如何相互作用的困難。
當一個人在玩遊戲時,通常會談論「能往前看到多少步」。而在我們這裡,這基本上是在問我們可以輕易獲知能在分支空間裡走多遠。作為計算上受約束的實體(computationally bounded entities),我們在分支空間有一定的「觸達範圍」。如果這個範圍不足以達到類似「獲勝點」的地方,那麼這個遊戲對我們來說就是「困難的」。
不過,這裡還有一個問題。在一個遊戲中「獲勝」的因素通常是在多路圖中達到一些特定的地方或區域。但這些地方或區域的定義通常是一些計算上在約束範圍內的東西(「只要看看是否有一行X」,等等)。這是對系統的某種「觀察」,它只是提取了完整狀態的一個特定的(計算約束內)採樣。然後,關鍵在於,這個採樣並沒有設法去「解碼多重計算的不可還原性」。
這裡有一個與熱力學的類比。在熱力學中,我們感知到「熱」和「熵增加」的事實是這樣的:我們的(粗粒度的)度量不能「解碼」導致系統中產生的特定狀態的不可還原的過程。同樣,我們認為「很難弄清楚如何贏得一場遊戲」的事實是這樣一個結果,即我們的獲勝判斷標準不能去「觀察遊戲的內部」和「解碼正在發生的事」,直到說它實際上成為只是選擇一個特定的、簡單徑直的路徑。相反,它是一個去經歷玩遊戲的多重計算不可還原的過程的問題,並且相對於對勝利的觀察,實際上是「看看它會落在什麼位置(seeing where it lands)」。
這裡也有一個與量子力學的類比。追溯玩一個遊戲的許多可能路徑,就像追尋量子力學中的許多歷史線程(threads),而獲勝的標準就像一個選擇某些線程的量子度量。在我們的「物理學計劃」中,我們想象我們作為觀察者是在分支空間中延伸的,通過我們對自己的單一經驗線程的信念,將不同的歷史線程「編織在一起」。在遊戲中,我們對單一經驗線的信念的類比,大概就是「重要的是誰贏誰輸;遊戲具體是怎麼玩的並不重要」。
為了與量子力學做一個更接近的類比,我們可以開始考慮將「多路遊玩」的不同部分結合起來,並試圖為這些部分如何結合起來制定一套「微積分學」。
我們在這裡討論的遊戲在某種意義上都是純粹的「技巧遊戲」。但在也有運氣因素的遊戲中,我們可以認為這導致了多路圖中的單一路徑「模糊化(fuzz out)」為一束路徑,以及本來是分支空間中的一個點變成了整個擴展區域。
在研究不同的具體遊戲和謎題時,我們經常不得不去研究一些相當簡化的案例,以便得到規模可控的多路圖。但是,如果我們研究非常大的多路圖,是否會有整體的規律性湧現?對於遊戲圖來說,是否存在某種潛在的「連續極限(continuum limit)」?
幾乎不可避免的是,如果我們看得「足夠詳細」,我們就會看到各種多重計算的不可還原性在發揮作用。但在我們的「物理學計劃」中,甚至在一般的多重計算範式中,一個關鍵的問題是,相關的觀察者並沒有看到那個層次的細節。就像熱力學或氣體定律從底層分子動力學中的「湧現(emergence )」一樣,底層計算的不可還原性的存在,不可避免地導致觀察者所能感知的簡單定律。
那麼,對於一個遊戲來說,「觀察者」的類比是什麼呢?至少在某些方面,它可以被認為是「獲勝」的判斷標準。那麼現在問題來了:如果我們只看這些標準,我們能不能推導出「物理定律」的類似物,而不敏感於其下的所有多重計算的不可還原的細節?
關於這一點,還有很多東西需要弄清楚,但也許可以從一個地方開始,看看各種遊戲中的分支空間和多路圖的大規模結構。在許多不同的遊戲中,一個基本的印象是,雖然分支圖的特徵可能在遊戲的「不同階段」之間發生變化,但在單個分支圖中,往往有某種統一性。如果我們看一下細節,可能有很多多重計算的不可還原性。但在某種「可感知的水平」上,圖的不同部分可能看起來很相似。這表明,即使已經採取了相當不同的行動,將人們帶到由分支圖定義的「遊戲空間」的相當不同部分,「遊戲的局部印象」在某一特定階段往往是相似的,。
但是,雖然分支圖的不同部分之間可能存在相似性,但我們看到的是,在一些遊戲和謎題中,分支圖會分成多個不相連的區域。這反映了遊戲中存在著不同的「守恆區(conserved sectors)」——玩家可以進入的遊戲空間區域,但隨後會被卡住(至少在一定時間內),就像在時空中事件視界(event horizons,校注:德國天文學家卡爾·史瓦西提出的涉及黑洞的概念,一旦光線或物質越過事件視界,就永遠無法逃脫了)可以阻止物理空間的不同區域之間的傳送。
我們在一些遊戲和謎題中注意到的另一個(相關的)現象是多路圖中的大「洞」:在圖中兩點之間有多條「遙遠」的路徑。當多路圖是密集連接的時候,通常總是有辦法通過附近的路徑改道來 「修復任何錯誤」。但是,當有一個洞時,這就表明人們最終會「致力於(committed)」某個行動的進程而不是另一個,而且要經過許多步驟才有可能到達與另一個行動進程所能到達的相同的地方。
如果我們假設在某個層面上,我們在多路圖中最終「觀察」到的是與評估輸贏相對應的那種粗粒度,那麼我們將不可避免地處理一個可能路徑的分佈情況。在沒有「洞」的情況下,這些路徑可能很接近,而且看起來很相似。但是當有洞的時候,可能會有相距甚遠的不同的路徑。而「屬於相同分佈部分」的遙遠路徑可能被認為是類似於量子疊加效應的事實。
遊戲中是否有類似於廣義相對論和路徑積分(path integral)的概念?為了清楚地表述這個問題,我們必須更仔細地定義「遊戲空間」的特徵。很可能會有因果圖(causal graph)的類似物。也很可能遊戲空間中也會有一個類似能量的概念,與遊戲空間中不同地方的「活動密度」相關。
那麼,引力現象的類似物將是這樣的:最好的遊戲的遊玩方式(即通過遊戲圖的測地路徑)將傾向於被高活動密度的存在所偏轉。換句話說,如果一個遊戲處於某種狀態時有很多事要做,那麼好的遊戲遊玩將傾向於「被拉向那個狀態」。在某種程度上,這並不令人驚訝:當遊戲圖中存在高密度的活動時,往往會有更多關於做什麼的選擇,因此,如果一個玩家經過那裡,就更有可能 「玩出一場精彩的遊戲」。
到目前為止,我們還沒有明確地談論遊戲的策略。但在我們的多重計算框架中,策略有一個相當明確的解釋:它是可能規則空間(rulial space)中的一個地方,在那裡,人們實際上是假設了一套關於如何構建多路圖的規則。換句話說,給定一個策略,人們就會在多路圖中選擇一些邊(或者在相關的多路因果圖中選擇一些可能的事件),而放棄其他的邊。
一般來說,談論「可能策略的空間」可能很困難,因為這就像談論「可能程序的空間」。但這恰恰是可能規則空間(rulial space)讓我們談論的東西。「策略空間」到底有什麼樣的「幾何結構」,將取決於我們如何選擇協調可能規則空間。但是,再一次,通過僅僅只看類似於博弈論中討論的那種東西,將傾向於實現某種程度的粗放(coarse-graining)——在這種程度上,我們可以預期所有各種標準的「結構化」的博弈論結果將普遍成立。
譯註:Rulial space是 Wolfram 自創的一個術語,意指所有可能的規則以及這些規則的所有應用方式所組成的空間。比如,從符號A開始應用符號替換規則{A → AB, BB → A},可以用下面的多路圖表示這個規則所有可能的應用方式:
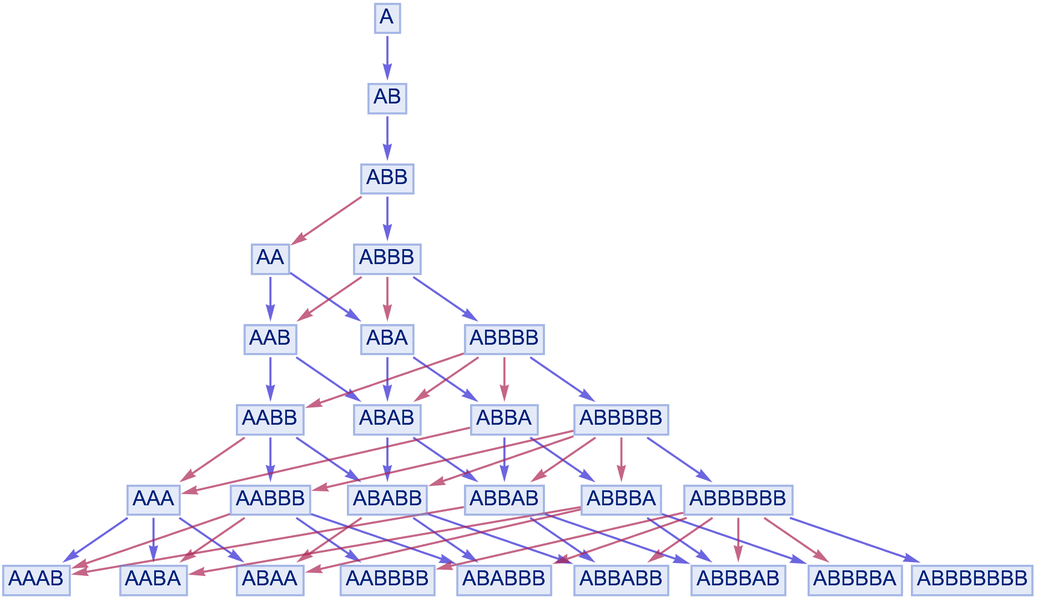
這個圖只畫出了前幾步,完整的圖應該是無限的
假設只有A、B兩個符號,只考慮長度最多為2的符號串,那麼所有這樣的可能的替換規則有
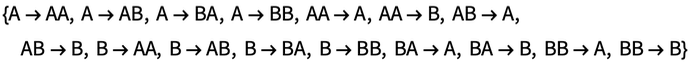
按照上面的方式畫出所有這些替換規則對應的多路圖,並把這些多路圖合併成一個圖,就構成了這個有限語境下的 Rulial space。
現在想象我們考慮的不僅僅是上面這些符號替換規則,而是宇宙中所有可能的規則,這個巨大的Rulial Space可以認為包含了一切”可計算的事物(everything that is computationally possible.)“。
推薦閱讀:The Concept of the Ruliad
個人筆記
Personal Notes
即使在小時候,我也從未特別喜歡玩遊戲或做拼圖。而這也許是我太像個科學家的一個標誌。因為只是選出特定的棋步對我來說總是顯得太武斷任意了。為了引起我的興趣,我需要一個更大的圖景,更加前後一致的認知敘事。
而現在,從某種意義上說,這正是我在這裡討論的對遊戲和謎題的多重計算方法帶給我們的東西。是的,能夠思考做出特定的動作是非常「人類視角化(humanizing)」的。但是,多重計算方法立即給人了一種連貫的全局觀,至少對我來說,理智上更令人滿意。
我在這裡討論的探索可以被認為是源於《一種新的科學》中的一個註釋。在《一種新的科學》的第五章中,我有一節首次介紹了多路系統。在那一節的最後一個註釋中,我討論了「遊戲系統」。

我在20世紀90年代做了這方面的研究——事實上,我現在發現1998年的一本關於井字棋的文件,其中得出了一些相同的結果

其中還有一個看起來很耐人尋味的關於井字棋的圖表:
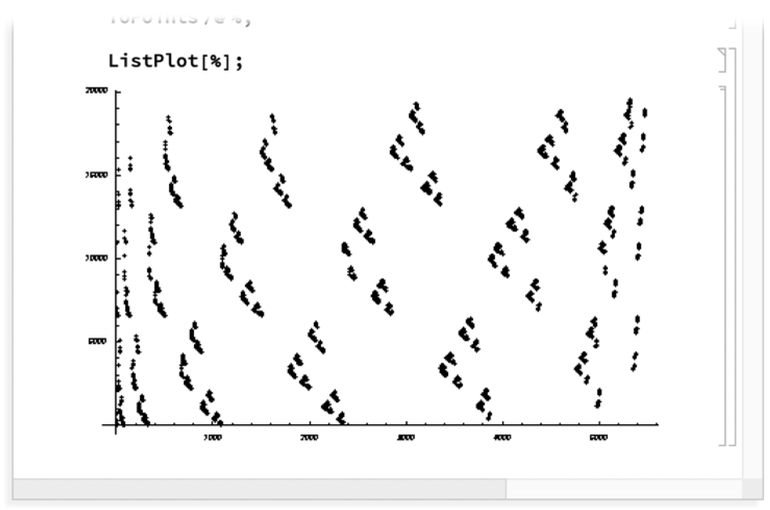
但在那個時候,我並沒有從我生成的這些遊戲相關的圖中得出什麼結論;它們只是顯得龐大而複雜。20年過去了,我沒有再多想這個問題。但後來在2017年,我的兒子克里斯托弗在玩一個叫《Rush Hour》的桌遊。

也許是家族傾向的表現,他決定構建其遊戲圖——得出了對我來說似乎是非常令人驚訝的結果。
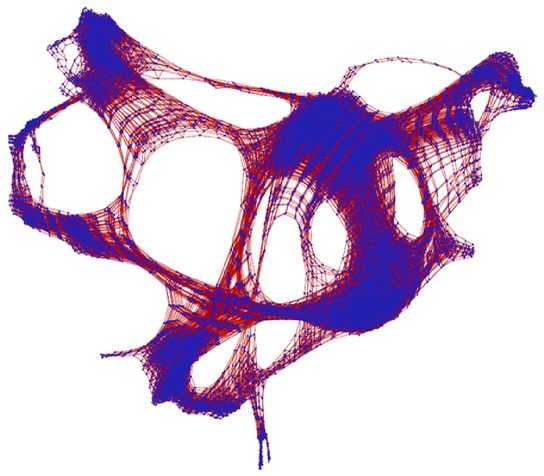
當時我並沒有試圖去理解這裡的結構,但我還是把它「歸檔」了,作為遊戲圖可以有「可見的大規模結構」的證據。
幾年後——2019年底——我們的物理項目正在進行中,我們已經意識到,量子力學和多路圖之間存在著深刻的關係。量子力學一直看起來是神秘的東西——純數學形式主義的抽象結果。但是,看到與多路系統的聯繫,開始暗示人們實際上能夠「理解量子力學」,因為它可以從一些具體的基礎結構中「機制地產生」。
我開始思考如何在一個直觀的層面上解釋量子力學。為此,我需要一個熟悉的類比:可以與多路系統聯繫起來的日常事物。我立即想到了遊戲。2020年9月,我決定考察一下游戲,以更詳細地探索這個類比。我很快就分析了井字遊戲和尼姆遊戲,以及簡單的滑動塊謎題和漢諾塔。但我想探索更多的遊戲和謎題。而且我還有其他項目要做,所以遊戲和謎題的多重計算分析被擱置了。
今年早些時候,漢諾塔又出現了,當時我把它作為一個生成類似證明的多路圖的例子,與我對元數學的物理化研究有關。最後,幾周前我決定是時候寫下我到目前為止所知道的關於遊戲和謎題的東西了——併產生了這裡的東西。
致謝
Thanks
感謝 Brad Klee 和 Ed Pegg 在本文給出的分析的最後階段提供的各種幫助——以及 Christopher Wolfram 在2017年的靈感和2020年的幫助。

日 | 落譯介計劃 是媒體實驗室落日間對一些有助於思考遊戲/電子遊戲的外文文本翻譯和推薦/索引計劃。(查看網站)。
遊戲-湧現-自然
David Krakauer 與達爾文下圍棋 Playing Go with Darwin (2020)
Jonathan Blow 遊戲設計的真如 Truth in Game Design (2011)
Michael Nielsen 重塑解釋 Reinventing Explanation (2014)
和厭氧菌的節目 E32 賽博文本中的幽靈作者
感謝支持落日間的朋友們!
歡迎讚賞或在愛發電贊助落日間