我們先從兩個簡單的問題入手:
什麼是紋素?
紋素是一個紋理的最小顆粒,即一個大小1024 * 1024 大小的紋理,它包含1024 * 1024 個紋素。
什麼是像素?
像素顯示設備上的最小顆粒,即一個大小1024 * 1024 大小的屏幕,它包含1024 * 1024 個像素。像素的多少與密度,決定了這塊屏幕分辨率的大小。
像素與紋素看起來非常相似,只不過一個主體是物理設備,一個主體是一張圖片。
在日常生活中的很多情況下,我們通常不會對像素與紋素概念做區分,我們也經常會說一張圖片的大小是 xxx 像素。但是在遊戲的概念中,這兩個概念很多時候都不應該被混淆。
舉個例子,假設一塊 4k 分辨率屏幕上,正正好好鋪滿了一張 4k 大小的圖片。此時紋理的紋素數量與屏幕的像素數量之比為 4k:4k = 1:1,即一個紋素對應一個像素。那麼如果此時將屏幕變更為 2k 分辨率的屏幕呢?此時紋理的紋素數量與屏幕的像素數量之比為 4k:2k = 2:1 即兩個紋素對應一個像素,此時像素明顯是不夠用的。
紋理顯示在屏幕上時,最理想的狀態就是每個屏幕像素對一個紋素。但是這並不現實,攝像機距離紋理的遠近決定了紋素對應像素的多少。當紋素對應像素的比例在某些值時,紋理在屏幕上顯示出奇怪的效果。


左:無mipmap;右:mipmap
miamap 機制會提前按照特定算法,生成不同縮放比例的紋理,並且根據紋素與屏幕像素的比例,來選擇不同縮放比例的紋理,儘量將紋素像素比維持在一個合理的大小。

左 128*128;中 64*64;右 32*32
由上圖可知:
mipmap0(128 * 128) ÷ 2 = mipmap1(64 *64)
mipmap0(128 * 128) ÷ 4 = mipmap2(32 *32)
mipmap 等級遞進(尺寸縮小)是以 2 的冪為係數的。
現在我們假設,一張 128*128 尺寸的紋理顯示在屏幕上 128*128 大小的區域中,此時紋素像素比為1。
然後我們將攝像機拉遠,直至該紋理顯示區域大小變為 64*64,此時紋素像素比為 128/64 = 2,即兩個紋素對應一個像素,這種情況下,我們理想的狀態是將紋理切換成 mipmap1,也就是尺寸為 64*64 的紋理,即一個紋素對應一個像素。換個角度就是說我們要將原始紋理大小縮小2倍,即 2的1次冪(mipmap1)。
繼續推算,當紋理顯示區域大小為32*32,我們可以計算出,原始紋理大小要縮小4倍,即2的2次冪(mipmap2)。
以此類推我們可以得到一個結論,我們會按照上述計算方式,選擇結果中2的冪數作為mipmap等級。
實際計算中,為了確認紋素與像素比,我們必然要提前計算兩個像素之間對應的紋素差值,還是上述例子,一張 128*128 尺寸的紋理顯示在屏幕上 64*64 大小的區域中,此時紋素與像素比值為 2:1,即兩個紋素對應一個像素,那麼兩個像素之間對應的紋素位置值(uv * 紋理分辨率)的差值即為2。
這種計算差值的操作,可以使用 gpu 提供的方法dFdx 與 dFdy (偏導數函數)來實現,如下圖:
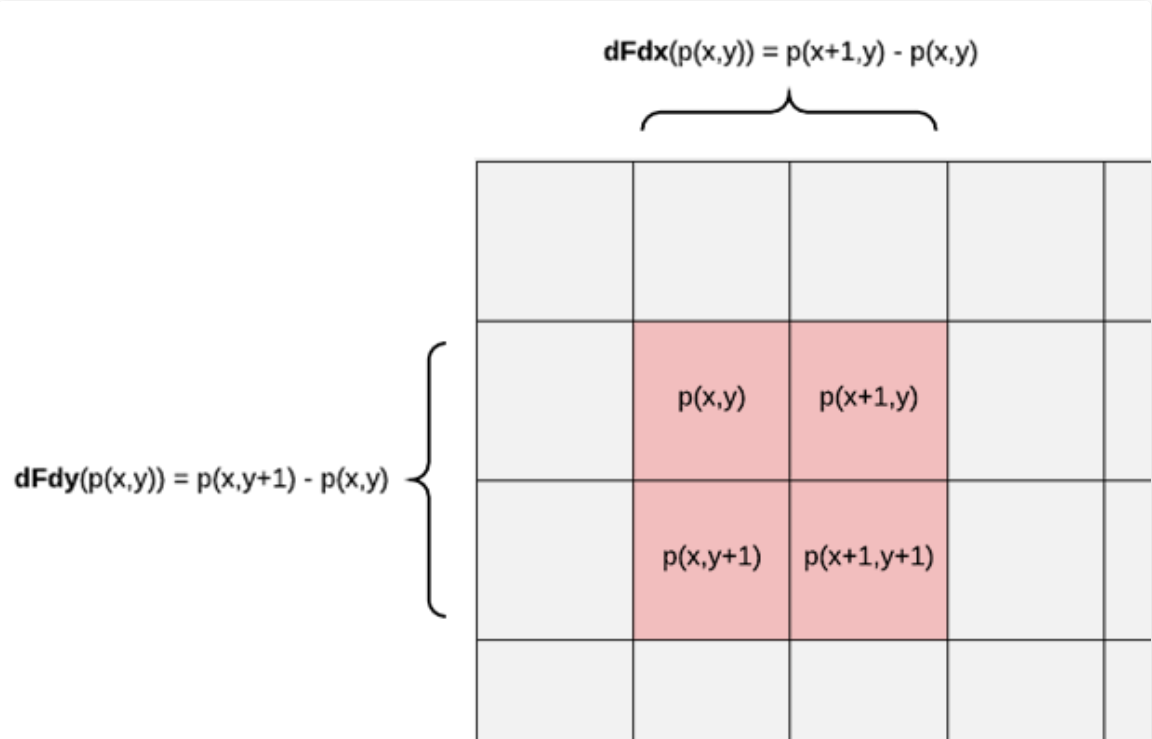
gpu 在渲染像素時,都是以 2*2 大小的像素塊為最小單位進行的(上圖中紅色塊),這就為偏導數計算提供了前提條件。每一塊 2*2 的像素塊中的相鄰像素會共同計算偏導數,然後這個偏導數會在這兩個相鄰的像素成員中共享。
在 shader 中計算偽代碼如下:

為了更直觀的理解上述 shader 中的計算方法,我們可以以下圖為參考:
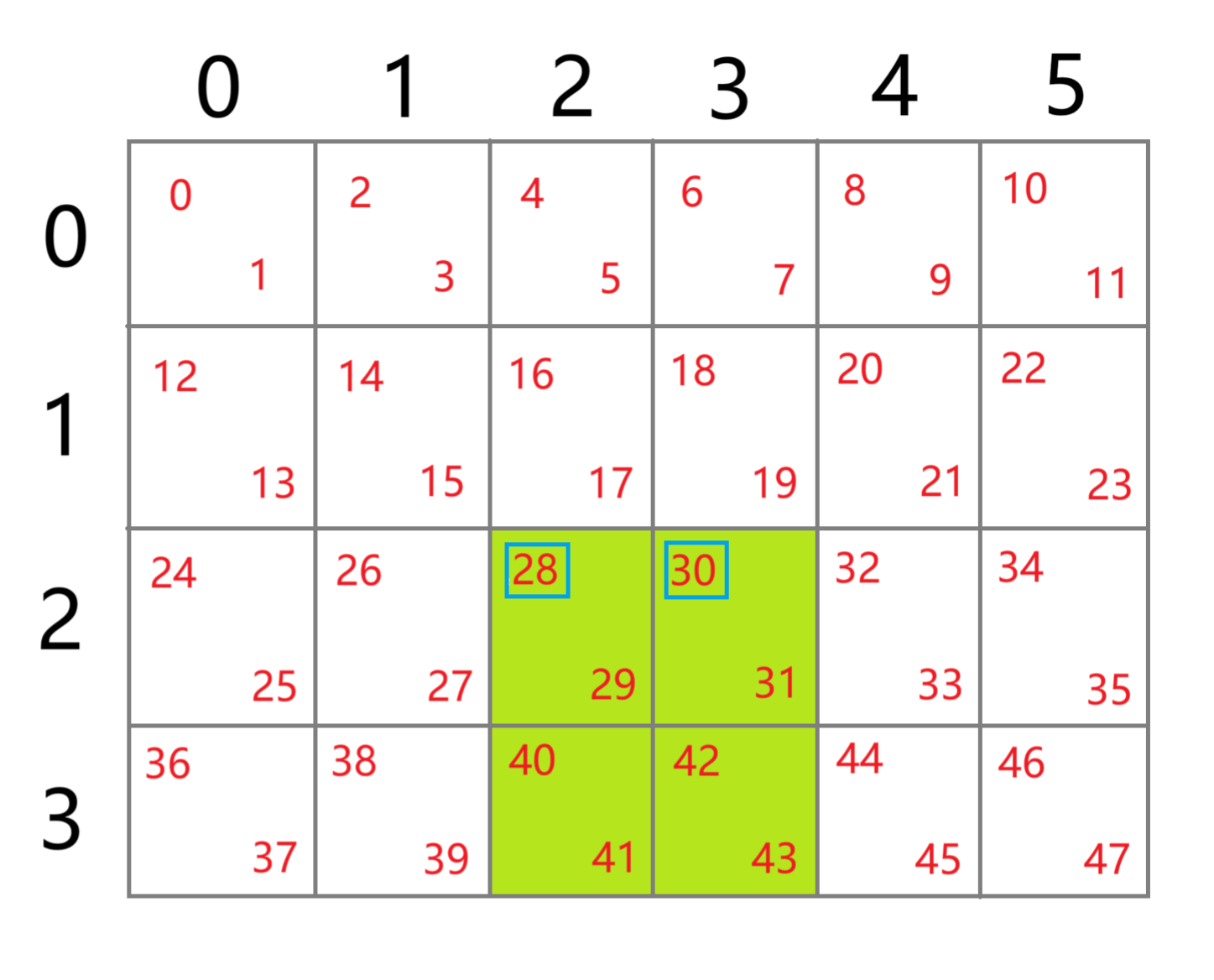
如圖,我們假設這是一個 6 * 4 = 24 大小的顯示器,灰框表示像素;這個屏幕上要顯示一張 6 * 8 = 48 大小的紋理,紅色數字表示紋素的編號。此時紋素與像素比為 48:24 = 2:1,即兩個紋素對應一個像素,所以圖中一個灰框中有兩個數字。我們假設被標記為綠色像素為 gpu 最小渲染單位:一組 2*2 像素塊。
由藍色框標出的數字相減,我們便得到一個值為 2 的橫向偏導數(ddx),這個偏導數的值代表了相鄰像素對應的紋素之間的差值,即兩個相鄰像素間相差多少紋素。
為了計算 mipmap 的 level 值,我們將的得到的偏導數值導入公式 ㏒b(Xⁿ),此公式計算時,偏導數由向量的點乘得到,原因是因為 uv 可能導致偏導數為負,所以使用向量對自身的點乘,得到向量長度的平方值。結合數值與這個公式 ㏒b(Xⁿ) ,即:
frag_size = 2 * 2 = 4
㏒2(√4) = ㏒2(4½) = 0.5 * ㏒2(4) = 0.5 * 2 = 1
所以我們要取 mipmap1 為最適合當前狀況的紋理等級。