原文鏈接
1993 年,id Software 發佈了 FPS 遊戲 Doom
,此遊戲一經發售就立刻成為現象級作品。如今也已被視為影響最為深遠的遊戲之一。
在 Doom 發售十年後的 2003 年,記者 David Kushner 出版了一本關於 id Software 的書《Doom 啟示錄》,並從此成為了關於 Doom 誕生的重要文獻。我在幾年前閱讀了《Doom 啟示錄》,其中的大部分內容已經被我遺忘。但唯獨有一個關於首席程序員 John Carmack 的故事一直縈繞在我心頭。我們會在後面詳細回顧這個故事,但簡單地說,在 Doom 的開發初期,Carmack 發現到他編寫的 3D 渲染器在渲染一些特定關卡的時候會慢到令人髮指。這是令人無法接受的,因為 Doom 理應是一款動力十足充滿激情的遊戲。Carmack 意識到這是一個觸及根基的問題,他需要找到一個更好的渲染算法來解決它。於是他開始閱讀論文,並最終實現了一個叫做 Binary Space Partitioning (BSP)的技術。這項技術在此之前從來沒有被應用在電子遊戲中,卻極大地提高了 Doom 引擎的運行速度。
這個 Carmack 將最尖端的技術應用在電子遊戲上的故事總是能打動我。對我來說,這正是 Carmack 之所以能成為一個傳奇的原因。儘管他在諸多方面都無愧於天才遊戲程序員的稱號,這段關於學術論文和 BSP 技術的歷史卻在我心中位列榜首。
當然了,這個故事讓人印象深刻的原因之一就是,Binary Space Partitioning 這個技術的名字聽起來很高深,感覺很難自己動手實現它。很長一段時間我都認為這是 Carmack 做出的一個智力飛躍,但我一直以來都沒有真正理解 BSP 是什麼,或者在 Carmack 決定使用它的時候這項技術有多先進,所以我一直都不確定,如果繪製一條從辛普森到愛因斯坦的智力光譜,Carmack 把 BSP 添加到 Doom 中這件事能排到哪?
同時我也好奇,BSP 的技術最初是從哪來,它最後又是如何被 Carmack 發現的。所以這篇文章不僅是關於 Carmack 和 Doom,也是關於 Binary Space Partitioning Tree (BSP 樹)這一數據結構的歷史。有趣的是,BSP 樹和許多其他的計算機技術一樣,源自軍方的研究活動。
沒錯:E1M1,也就是 Doom 的第一關,由美國空軍為您呈現。
VSD 問題
BSP 樹的設計是為了解決計算機圖形學中一個非常棘手的問題: 為了渲染一個三維空間,給定一個視角的情況下,渲染器必須能夠區別出什麼能被看到而什麼不能。 如果你有很多時間的話,這不是什麼大問題,但一個實時的遊戲引擎需要在一秒內判斷至少 30 次。
這個問題有時會被稱作可見表面決策(Visible Surface Determination)。 Michael Abrash,一個和 Carmack 一起開發 Quake(id Software 在 Doom 之後的作品)的程序員, 曾經在他著名的《圖形編程黑皮書》(Graphics Programming Black Book
)中提到 VSD 問題:
我想談一下我認為最棘手的 3-D 問題:可見表面決策(在每個像素上繪製正確的表面), 以及它的近親問題,多邊形剔除(通過儘快剔除不可見的多邊形來加速可見表面決策)。 為了表述的簡潔,我在下文會用 VSD 來同時指代這兩者。 為什麼我會認為 VSD 是 3-D 技術中最棘手的挑戰? 雖然類似紋理映射這種光柵化相關的問題也很有趣且重要,但他們的應用範圍相對有限, 而且可以被移交給諸如 3-D 加速器之類的硬件來處理; 同時,他們的處理難度只和屏幕的分辨率相關,所以相對來說比較容易應對。 然而,VSD卻是一個開放性的問題,已經有幾十種應用方法。 最重要的是,如果不能用恰當的方法應對,VSD的規模會隨著場景的複雜度呈平方甚至立方級數增長, 所以它很快就會變成渲染真實世界的一個限制因素。
Abrash 所談及的是在 90 年代末期時想要解決 VSD 問題的難度。 此時 Doom 的成功已經證明普通玩家想要在他們的家用電腦上玩到圖形密集性遊戲(graphically intensive games)。 在 90 年代初期 id Software 該開始發行遊戲的時候, 遊戲開發必須精打細算,以圖能夠在那些不是為了遊戲而設計的電腦上運行。 本來這些電腦只會用來運行一些文字處理軟件或者表格應用之類的小玩意。 為了讓遊戲能跑得起來——特別是 id Software 在 Doom 之前開發的一些 3D 遊戲——id Software 必須非常有創造力, 因為在這些遊戲中,他們的關卡設計需要保證 VSD 問題易於解決。
舉例來說,id Software 在 Doom 之前發售了一款叫做 重返德軍總部 3D 的遊戲。 在這款戲中,每個關卡的牆壁都是軸對齊(axis-aligned)的。 換句話說,在 重返德軍總部 的世界裡,你只能有南北朝向或者東西朝向的牆。 每面牆的間隔必須是格子的整數倍,也就是說走廊要麼是一格寬, 要麼是兩格寬,但絕對不可能是 2.5 格寬。 儘管這種限制使得軟件團隊設計的關卡看起來都很相似, 但卻令 Carmack 對 重返德軍總部 渲染器的編寫工作變得輕鬆了許多。
重返德軍總部 通過從屏幕向虛擬世界發射光線來解決 VSD 問題。 基於光線的渲染器一般叫做「光線投射渲染器」(raycasting render)。 這種渲染器通常都很慢,因為要通過光線投射來解決 VSD 問題需要找到光線和虛擬世界世界中的某個物體第一次相交的位置,而這通常會帶來大量的計算。 但是對 重返德軍總部 來說,因為所有的牆面都是軸對齊的,所以光線只能在網格線上和牆壁相交。 因此渲染器要做的事情就只是檢查這些交點。 渲染器會從離玩家最近的交點開始檢查,然後是次近的交點, 以此類推,最終當它遇到一面牆時就停止檢查。 通過這種方式,只需要一點微不足道的代價就可以解決 VSD 問題, 因為這種算法就只是從每一個像素射出一條光線,令光線一直行進直到擊中一面牆, 而光線的行進對 CPU 週期來說則非常廉價。 實際上,因為所有牆體的高度都是一樣的,所以對每一列像素都只需要發射一條光線即可。
這個渲染技巧足以讓 重返德軍總部 在專用的圖形卡問世之前就可以運行在性能孱弱的家用 PC 上, 但這個方法無法套用在 Doom 上,因為 id 團隊當時已經決定他們的新作必須支持更多新特性, 包括斜向的牆壁、樓梯、不同高度的單元格等等。 光線投射方案不再可行,因此 Carmack 編寫了一個新的渲染器。 重返德軍總部 這種為每一列像素髮射一條光線的渲染器是「圖像優先」(image-first), Doom 的渲染器則是「物體優先」(object-first)。 這意味著不同於遍歷所有屏幕上的像素來決定它們的顏色, Doom 的渲染會遍歷場景中的所有物體,並將它們投影到屏幕上。
對於物體優先的渲染器來說,解決 VSD 問題最簡單的辦法就是使用 z 軸緩存(z-buffer)。 每次你要把一個物體投影到屏幕上並繪製相應的像素時,你都可以進行一次檢查。 如果你要繪製的部分比已經繪製完成的物體距離玩家更近,你就可以覆蓋當前的像素。 否則你就跳過繪製過程。 這個方法非常簡單,但問題是 z 軸緩存需要很多內存,而且渲染器很可能會花費很多 CPU 週期來投影一些玩家永遠都看不到的幾何體。
在 1990 年代早期,基於 z 軸緩存的方案還有一個問題:當時 IBM 兼容機使用了一個叫做 VGA 的圖形調製系統,這導致對輸出緩存的寫入操作非常昂貴。 如果你繪製的像素在之後會被覆蓋重繪,這些被浪費的時間就會大大拖累渲染器的性能。 因此比較理想的做法是,優先繪製離玩家最近的物體,然後是那些物體之後的物體, 直到所有的像素都繪製完成。 此時渲染器需要停止渲染,避免把時間花費在那些玩家永遠都看不到的遠處的物體上。 但是把物體由近及遠地排序,實際上和 VSD 是等價的。 也就是說,我們又回到這個問題:玩家到底能看到什麼?
最開始,Carmack 嘗試通過 Doom 的關卡布局來解決這個問題。 他的渲染器會首先繪製玩家當前所在房間的牆壁,然後再繪製能被玩家看到的相鄰房間的牆壁。 如果每個房間都是凸多邊形(譯註:即房間內的牆壁不會相互遮擋),那麼這個問題就可以被解決。 那些不是凸多邊形的房間則可以被切割成多個凸多邊形的區域。 這個算法被成功的運用在 Doom 發售三年之後的 毀滅公爵 3D 上,此時 CPU 已經有了更高的性能。 但是在 1993 年,在當時可用的硬件平臺上使用這個算法的 Doom 渲染器在處理比較複雜的關卡時則會捉襟見肘, 尤其是當凸多邊形區域之間會互相嵌套的場景更是如此,比如圓形樓梯就肯定會導致這種情況。
就在 id 團隊意識到 Doom 引擎不夠快的時間點前後,id Software 收到了任天堂的委託, 要把 重返德軍總部 3D 移植到 SFC 平臺,而 SFC 甚至比當時的 IBM 兼容機性能還要弱。 結果證明,光線投射版本的 重返德軍總部 渲染器沒辦法在 SFC 上快速運行, 所以 Carmack 開始尋找一個更好的算法。 事實上 Carmack 正是為了 SFC 版本的 重返德軍總部 才開始研究和實現 BSP 算法的。 其實 重返德軍總部 的問題要更容易處理一些,因為它的牆壁都是軸對齊的; Doom 的情況要更復雜一些,但是 Carmack 意識到 BSP 樹也可以解決 Doom 的性能問題。
Binary Space Partitioning
BSP 方法可以通過把一個 3D 場景提前分割成不同區域來讓 VSD 變得易於解決。 想象你在空間中劃出一條線(在 3D 空間中則是一個平面), 同時你知道玩家或攝像機位於這條線的哪一邊, 而且你還知道位於另一邊的任何物體都無法遮擋這一邊的物體。 只要你這樣重複分割這個空間,最終你會得到很多區域, 而且你可以知道不同區域之間的遮擋關係。
最早關於這種分割 3D 空間方法的論文出自美國空軍的研究者。 他們嘗試論證計算機圖形技術有沒有足夠的效率用於飛行模擬。 它們在一篇 1969 年的一篇叫做 Study for Applying Computer-Generated Images to Visual Simulation 的報告中公開了他們的發現。 報告指出計算機圖形技術可以用來訓練飛行員,但同時也預警了 VSD 帶來的實現上的複雜度:
在實時計算圖像時,我們要面對的最重要的問題之一便是優先級問題,或是隱藏線問題。 在我們的日常環境的透視中,這個問題輕而易舉就可以解決。 一個非透明物體上的點,會遮蓋住相同視線上所有更遠的點。 對計算機來說,這個問題卻異常艱鉅。 通常來說,解決優先級問題所需要的計算量會隨著周圍環境的複雜度成指數級增長, 並很快就會超出透視圖像計算的負載範圍。
研究人員提到一個算法,這個算法可以生成一個被我稱為遮蔽矩陣(occlusion matrix)的矩陣。 據說這個算法曾被運用在 NASA 的一個項目中。 研究人員指出,如果一個平面將一個場景分為兩塊區域,那麼位於不同區域的所有物體間的優先級問題 都可以藉助這個平面來解決。 通常來說你可能需要自己將這個平面添加到場景中, 但是通過一些特定的幾何方法,你也可以直接使用場景中的物體已有的平面。 他們給出瞭如下圖的一個示例。 P_1, P_2 和 P_3 是分割平面。 如果攝像機在一個平面的正面(“true” side),那麼矩陣中 p_i 的值就是 1 。 基於這三個平面和視點位置,這個矩陣可以表現出這三個物體之間的關係: 如果一個物體 aiai 遮擋了物體 ajaj,那麼矩陣中的 A_ij=1。
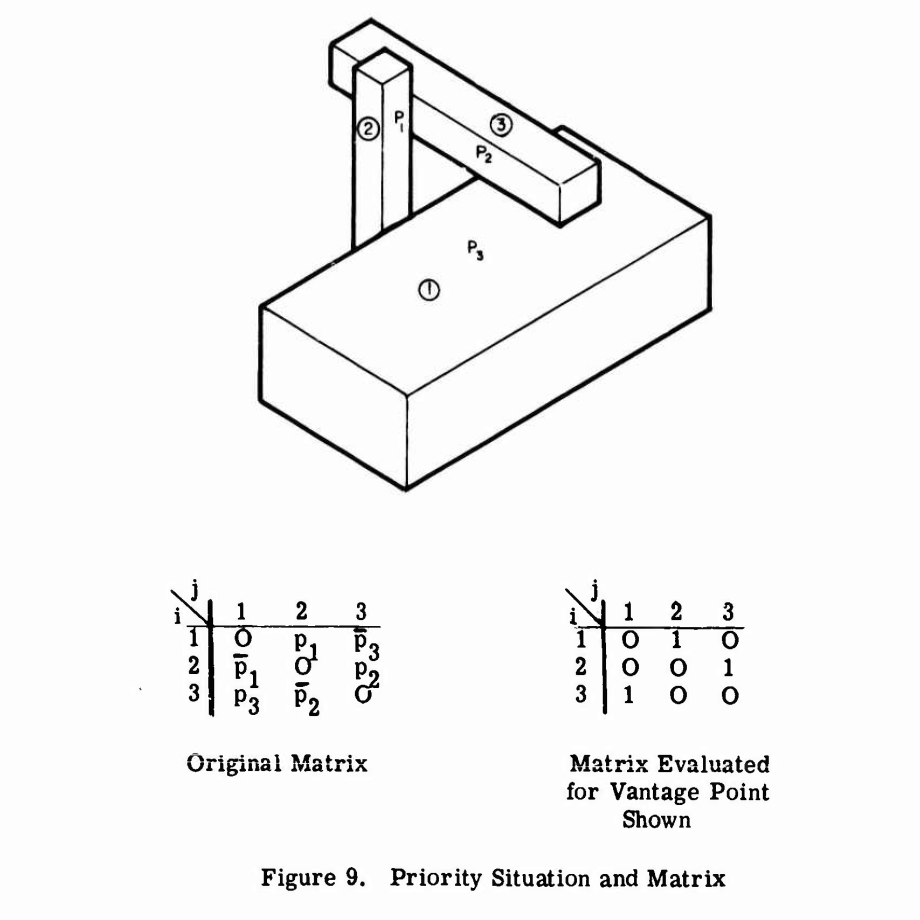
① ② ③ 為物體編號,P_1, P_2, P_3 為平面
研究人員提出,這個矩陣可以事先實現在硬件中,並對每一幀重新計算。 基本上來說,這個矩陣就是一個大型的開關,或者說是一種預置的 z 軸緩存。 當繪製一個物體時,如果要繪製的部分對應的這一列中有一個 1, 且對應的行已經被繪製,那麼這部分物體就不應該被繪製。 (譯註:以上圖為例,物體① 的列中有一個 1,說明它被其他物體(物體③)遮擋。 如果物體③ 已經被繪製了,那麼已經繪製的物體③就不應該被重繪)
這個矩陣帶來的一個主要的弊端是,如果要表現一個包括 nn 個物體的場景, 那麼這個矩陣的大小就會變成 n2n2 。 因此,研究者隨後便探索是否存在一種方法可以將遮蔽矩陣表達為一個「優先級列表」, 這樣之須臾一個長度為 nn 的列表就可以確定所有物體的繪製順序。 他們立刻就注意到對如上圖所示的這種特定場景來說,這種順序都是不存在的 (因為他們存在循環遮擋的物體)。 所以他們花費了大量的時間去從數學上區分出尋常(proper)和非尋常(improper)的場景。 最終他們得出結論:至少對於尋常場景來說,這個優先級列表是可以生成的, 而對場景設計者來說避免創造非尋常場景也並不困難。 這個 1969 年的研究最首要的貢獻也許是,它指出了通過分割平面來對物體排序是可行的,至少在理論上是可行的。
直到 1980 年的一篇叫做 On Visible Surface Generation by A Priori Three Structure 的論文才提出 一個切實的算法來真正地完成這項工作。 這篇出自 Henry Fuch,Zvi Kedem 和 Bruce Naylor 的論文引入了 BSP 樹。 論文作者聲稱,他們提出的這個數據結構是「另一個技術方案的替代方案,這個方案提出於十年前, 卻因為一些困難無法被廣泛應用的。」在這裡他們引用了 1969 年那個源自美國空軍的研究。 BSP 樹一旦被構成就可以方便的提供場景中物體的優先順序。
Fuchs, Kedem, 和 Naylor 非常詳細地解釋了 BSP 樹是如何工作的, 但我會在這裡提供一個沒那麼正式但更簡潔的說明。 (譯註:原作這裡的說明其實比較難懂,因此譯者在這裡參考維基百科中的示例進行說明,如有紕漏請多斧正。)
需要說明的是,在 BSP 算法中出現的平面都是雙向平面,即需要指定一個「前方」。 「前方」可以粗略的理解為在被玩家看到時面向玩家的方向。 這個方向一旦確定便無需更改,並不會隨視點的位置變化而變化。
BSP 樹的構建
BSP 樹的構建過程如下:
- 從將場景選取一個多邊形 P,將它作為根節點 N。
- 對於剩下的多邊形
- 如果它全部都在 P 的後方,則將它放在 N 左邊的列表中
- 如果它全部都在 P 的前方,則將它放在 N 右邊的列表中。
- 如果它只有一部分在 P 的前方,則將它分隔為前後兩部分,分別放入 N 左右兩邊的列表中。
- 對 N 左右兩邊的列表重複以上操作。
對 BSP 樹中的一個節點,所有左側子節點都在它的後方,而所有右側子節點都在它的前方。 下圖是一個具體的示例,可以詳細展示這個過程的具體步驟。
重複以上過程,直至所有的多邊形都被選為節點。
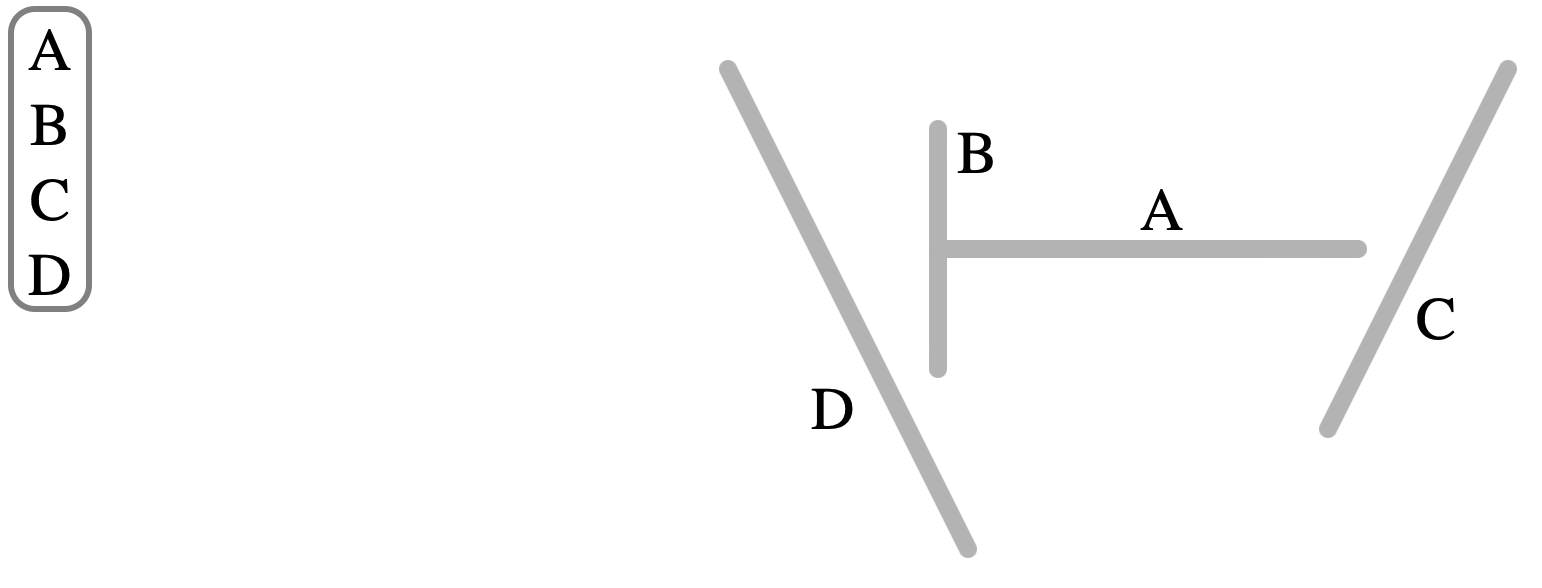
場景中有 A B C D 四個多邊形。
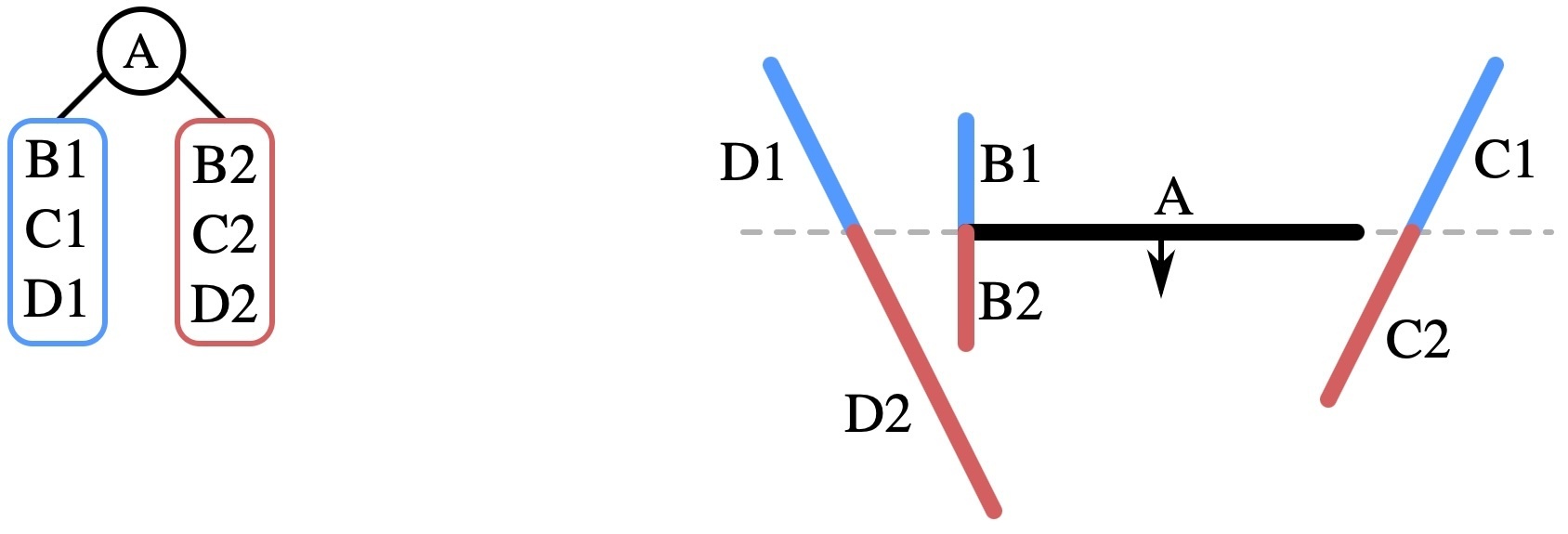
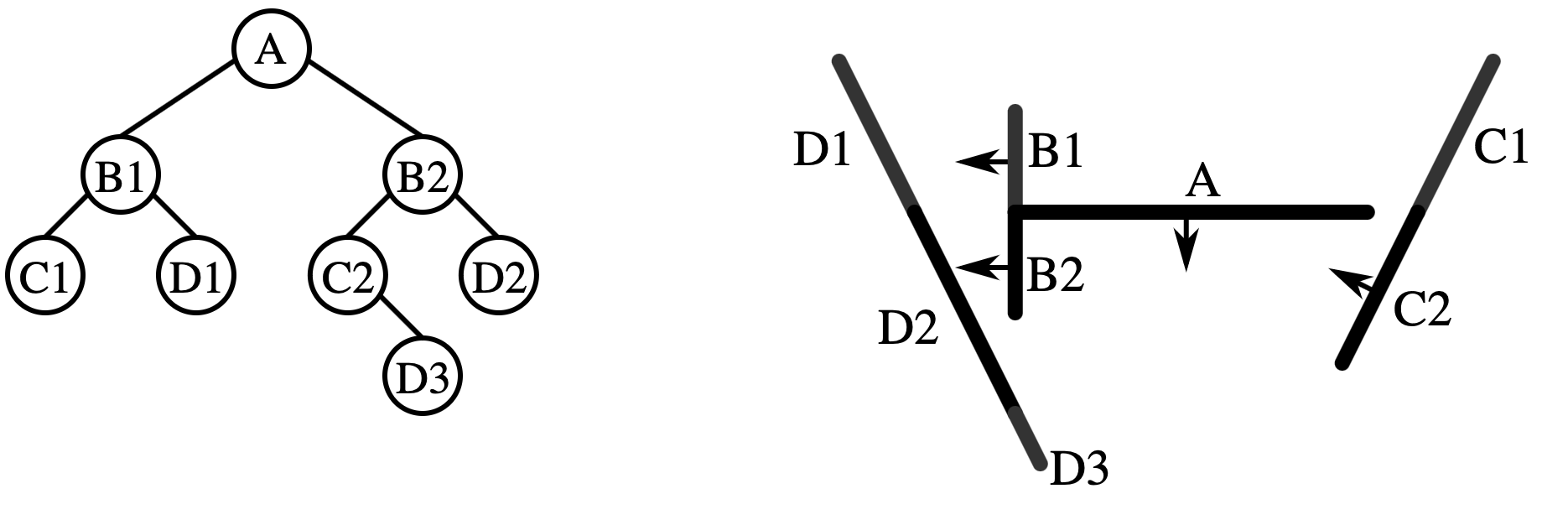
選取 A 作為第一個節點。由於 B C D 三個多邊形都被 A 分割,因此將他們分割為 B1 B2 C1 C2 D1 D2 六個多邊形,其中 B1 C1 和 D1 位於 A 的後方,B2 C2 和 D2 位於 A 的前方, 分別將它們放入 A 左右兩邊的列表中。
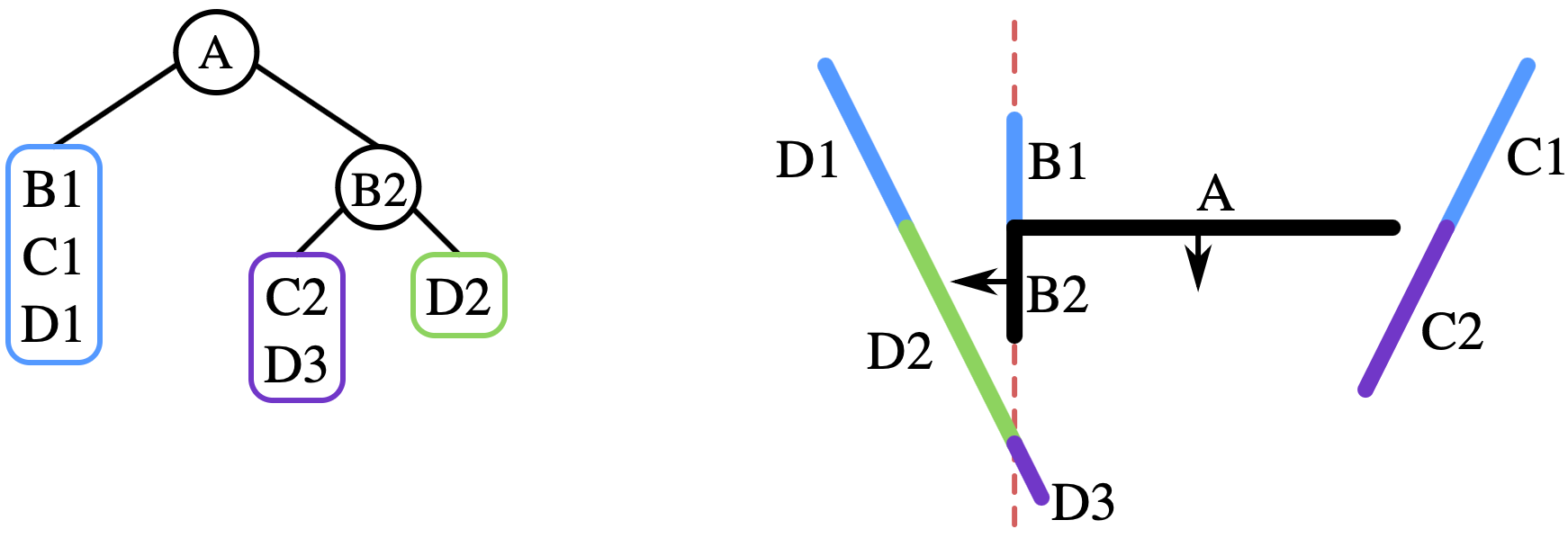
從 A 右邊的列表選取一個多邊形 B2 作為節點,此時 C2 完全位於 B2 的後方,因此放入 B2 左邊 的列表。D2 則被 B2 重新分割成 D2 和 D3 兩部分, 分別放入 B2 左右兩邊的列表。

重複以上過程,直至所有的多邊形都被選為節點。

場景中有 A B C D 四個多邊形。

選取 A 作為第一個節點。由於 B C D 三個多邊形都被 A 分割,因此將他們分割為 B1 B2 C1 C2 D1 D2 六個多邊形,其中 B1 C1 和 D1 位於 A 的後方,B2 C2 和 D2 位於 A 的前方, 分別將它們放入 A 左右兩邊的列表中。

從 A 右邊的列表選取一個多邊形 B2 作為節點,此時 C2 完全位於 B2 的後方,因此放入 B2 左邊 的列表。D2 則被 B2 重新分割成 D2 和 D3 兩部分, 分別放入 B2 左右兩邊的列表。

重複以上過程,直至所有的多邊形都被選為節點。
1 / 4
BSP 的使用
在渲染多邊形時有一種叫做「畫家算法」的方法,核心思想是由遠及近地繪製像素, 如此一來近處物體的像素就會將遠處物體的像素覆蓋,由此來實現遮擋的效果。 在 BSP 中這種方法體現在在渲染一個節點 N 時,根據視點 V 相對於 N 的位置, 要先渲染 N 左邊或右邊的節點。具體規則如下:
- 如果 N 是葉子結點(N 沒有子節點),則直接渲染 N
- 如果 V 在 N 的前方,
- 繪製 N 左邊的節點(對應多邊形位於 N 後方)
- 繪製 N
- 繪製 N 右邊的節點(對應多邊形位於 N 前方)
- 如果 V 在 N 的後方
- 繪製 N 右邊的節點(對應多邊形位於 N 前方)
- 繪製 N
- 繪製 N 左邊的節點(對應多邊形位於 N 後方)
下面以下圖為例詳細說明其操作步驟:
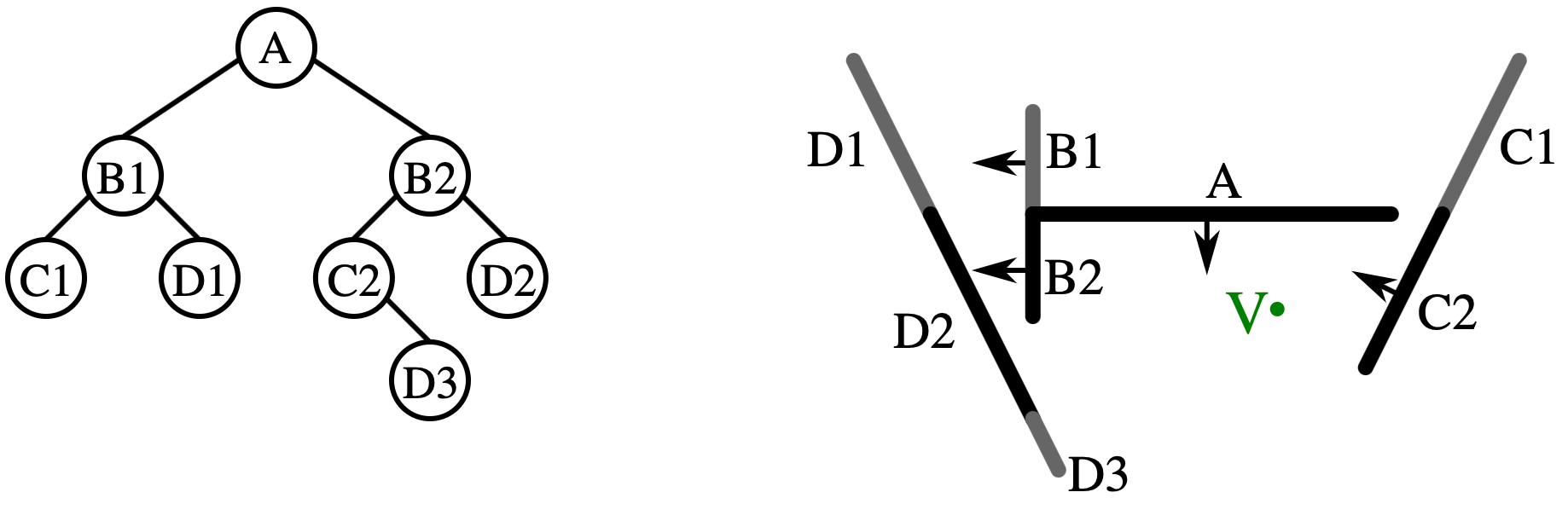
這裡的 BSP 樹的根節點為 A ,因此我們從 A 開始繪製多邊形。攝像機視點 V 位於 A 的前方,所以我們先繪製 A 後方的多邊形,即 {B1,C1,D1}。 接著繪製 A,此時 {B1,C1,D1} 中被 AA 遮擋的部分的像素就會被 A 的像素覆蓋。 最後被繪製的是 A 前方的多邊形,即{B2,C2,D2,D3}。 同樣的,此時如果有多邊形遮擋了 A ,它的像素也會覆蓋 A。
類似地,對 {B2,C2,D2,D3} 的繪製從 B2 開始。由於 V 在 B2 的後方, B2 會遮擋位於它前方的多邊形,並可能被位於它後方的多邊形遮擋。 因此我們需要先繪製 B2 後方,即 BSP 樹中 B2 右邊的節點,即 {D2},接著繪製 B2,最後是位於 BSP 樹中位於它左邊的 {C2, D3}。(譯註:對 BSP 的解釋至此結束。此處開始為原文內容。)
正如 Fuchs, Kedem 和 Naylor 多次強調,BSP 樹真正簡潔之處在於它只需構建一次。 也許這聽起來有些意外,然而只要場景內的物體沒有移動,不論視點位置如何變動, 對一個場景的渲染都只需一棵 BSP 樹。 這也是為什麼 BSP 樹對實時渲染如此有用:最困難的工作都在於構建 BSP 樹, 而這個過程完全是提前完成的,無需發生在渲染過程。
Fuchs, Kedem 和 Naylor 還提出了一個需要進一步回答的問題, 即什麼樣的 BSP 樹才是一棵「良好」的 BSP 樹。 BSP 樹的質量主要取決於你選取的首個用於構建 BSP 樹的多邊形。 如前文所說,如果你選取的多邊形和其他多邊形的平面相交,你需要用它來分割所有與其相交的多邊形。 如果這種操作頻繁發生,那將大大增加場景中的多邊形數量。
那篇 1980 年的論文的作者之一, Bruce Naylor,在 1993 年發表了另一篇論文討論了這個問題, 論文題目為 Constructing Good Partitioning Trees 。 根據 Carmack 的一位 id Software 合夥人 John Romero 的說法, 這篇論文是 Carmack 在嘗試為 Doom 實現 BSP 樹時所參考的論文之一。
Doom 中的 BSP 樹
還記得 Carmack 最初設計的 Doom 渲染器嗎? 在那個版本中 Carmack 嘗試用從當前房間延伸至相鄰房間的方法來決定渲染順序。 用 BSP 樹來決定渲染順序效果更好,因為它避免了渲染器可能會重複進入某個房間或區域的情況, 而這種情況會浪費很多 CPU 週期。
「給 Doom 添加 BSP 樹」意味著在操作層面上為 Doom 的關卡編輯器添加一個 BSP 樹的生成器。 每當一個 Doom 的關卡設計完成,就會根據關卡的幾何結構生成一棵 BSP 樹。 據 Fabien Sanglard 所說,為一個關卡生成 BSP 樹大約需要 8 秒鐘,而為整個原版 Doom 的所有 關卡生成 BSP 樹則需要大約 11 分鐘。 有時 BSP 樹的生成可能會花費更多的時間, 因為 Carmack 的生成算法會嘗試找出一個「良好」的 BSP 樹。 一個 8 秒鐘的延遲在遊戲運行時是不可接受的,但是對線下場景來說這點時間完全值得等待, 尤其是考慮到 BSP 樹對渲染器性能帶來的巨大收益。 對每一個關卡生成的 BSP 樹都會作為關卡數據的一部分被載入遊戲。
Carmack 對 1980 年的論文所提出的 BSP 樹算法做了一個翻轉, 因為 Doom 啟動並將 BSP 樹載入內存後,渲染器會通過 BSP 樹由近及遠地繪製物體,而非由遠及近。 在 1980 年的論文中,Fuchs, Kedem 和 Naylor 展示瞭如何通過 BSP 樹來實現由遠及近的畫家算法, 但是畫家算法會涉及到很多重複繪製,這對 IBM 兼容機來說是巨大的性能代價。 因此 Doom 的渲染器選擇從距離玩家最近的物體開始繪製。 這個轉變很容易在 BSP 樹中實現,因為你只需要在繪製每一個節點時使用相反的決策順序即可。 為了避免已經繪製的多邊形被遠處的多邊形的像素所覆蓋,Doom 渲染器使用了一種內存需求更小的隱式 z 軸緩存。 它包括一個數組來記錄水平方向上的遮擋關係, 還有兩個數組分別用來記錄從上至下和從下至上的垂直方向的遮擋關係。 Doom 渲染器不需要使用真正的 z-buffe的原因是,它在技術上並不是完全 3D 化的遊戲。 這種簡陋的數據結構之所以能夠奏效是因為某些特定的東西絕對不會在遊戲中出現: 它只需要水平方向的遮擋數組是因為遊戲中沒有傾斜的牆壁, 只需要垂直方向的遮擋數組則是因為遊戲中不會出現一個窗戶在另一個窗戶的上方這種情況。
最後就只剩下一個問題,那就是如何在已經提前生成 BSP 樹的靜態關卡場景中處理移動的角色。Doom 中的敵人無法作為 BSP 樹的一部分,因為他們會移動,而 BSP 只能處理不會移動的幾何結構。 所以 Doom渲染器會先繪製靜態的關卡結構,記錄已經繪製的屏幕區域 (這裡用到了另一種內存高效的數據結構)。 接著它會由遠及近地繪製敵人,並將它們裁切到遮擋他們的屏幕區域內。 這個過程不如 BSP 樹的渲染過程高效,但由於通常來說敵人的數量都要比關卡的幾何結構少很多, 因此這裡的速度並不是什麼大問題。
對 BSP 樹的使用是一個關鍵性的勝利。 顯而易見,Carmarck 發現利用 BSP 樹完美地解決他的問題這一過程是極其乾淨漂亮的。 但問題是,這算是一個天才級別的動作麼?
在 Fabien Sanglard 關於 Doom 引擎的精彩著作中,它引用了 John Romero 關於 Bruce Naylor 的論文(Constructing Good Partitioning Trees)的評論。 John Romero 認為這篇論文主要是關於利用 BSP 樹來移除 3D 模型背面的技術, 而 Carmack 認為這技術可以為 Doom 所用,於是他就實現了它。 這段描述是一種對 Carmack 的稱讚,因為它暗示了在其他人還在使用 BSP 來渲染靜態場景時, Carmack 已經看出這項技術可以被用在實時的電子遊戲中。 類似的評價也出現在了《Doom 啟示錄》中: Kushner 暗示了 Carmack 閱讀了 Naylor 的論文之後 問自己,「萬一你不只能用 BSP 來創造 3D 圖像,還能用它來創造整個虛擬世界呢?」
但這種說法忽略了 BSP 樹的歷史。 在美國空軍的研究者首次意識到通過分割空間可以加速渲染時, 他們就對加速實時渲染過程產生了興趣, 畢竟他們本來就在嘗試制開發一個飛行模擬器。 那個飛行模擬器的樣例在 1980 年 BSP 的論文中再次出現。 Fuchs, Kedem 和 Naylor 談論了 BSP 如何在飛行模擬中發生作用: 飛行員可以通過飛行模擬器在同一個機場中反覆練習降落, 由於這個過程機場的幾何結構不會變化,因此只需要生成一次 BSP 樹。 很顯然,他們當時就是在考慮實時模擬。 在論文中關於研究動機的部分,他們甚至提到了為什麼實時圖形系統需要在 1/30 秒內生成一張圖片。
所以,Carmack 並不是第一個想到將 BSP 樹運用在實時圖形模擬場景中的人。 當然,誕生這個想法和將它付諸實踐完全是兩回事,但就算是在實現層面, Carmack 所參考的內容很可能也比通常所認為的要多。 至少在本文撰寫時,維基百科關於 BSP 樹的頁面中依然有信息指出 Carmack 參考了 Chen 和 Gordon 發表於 1991 的論文 Computer Graphics: Principles and Practice。 此論文在 1990 年亦曾作為教材使用。 儘管關於此條信息並沒有明確的參考鏈接,但它很可能是屬實的。 Chen 和 Gordon 這篇 1991 年的論文中給出了基於 BSP 樹的由近及遠的渲染方法, Doom 所使用的方法基本與其相同,其中包括我所說的「隱式z-buff」數據結構。 在教材版本中則全面介紹了 BSP 樹,並提供了包括構建和渲染 BSP 樹的偽代碼。 (我曾有幸在我大學的圖書館中略讀過此教材的 1990 版。) Computer Graphics: Principles and Practice 是計算機圖形學的經典教材,所以 Carmack 很可能也擁有一本。
無論如何,Carmack 發現自己面臨一個全新的問題——我們怎麼才能在一個連支持浮點運算的 CPU 都沒有的計算機上運行一個 FPS 遊戲? 他做了研究,證明了 BSP 樹是一個對實時電子遊戲非常有用的數據結構。 即使 BSP 樹在十年前就已經被髮明, 而在 Carmack 閱讀到 BSP 樹的相關文獻時這項技術已經被充分研究, 我依然認為這項工作是令人印象深刻的壯舉。 也許真正值得我們慶祝的成就是,Doom 遊戲引擎作為一個整體是如此乾淨漂亮。 我們不應該忽略的是, VSD 問題只是 Carmack 為了讓 Doom 正常工作所需要解決的眾多問題中的一個。 在此同時,他還能夠研究和實現一個大部分程序員聞所未聞的複雜數據結構, 這些才真正體現出他在技術上的天才之處,以及對完美作品的追求。