第一题不说了
ABC
第二题可以看到按钮A与按钮C是对称的，即解题步骤中将A和C交换也是可以的。
我们可以采用逆推的方法，从结果往回推
可以得到两种结果:CBAC和ABAC再根据对称性，交换A和C，则可以得到另外两种结果ABCA和CBCA
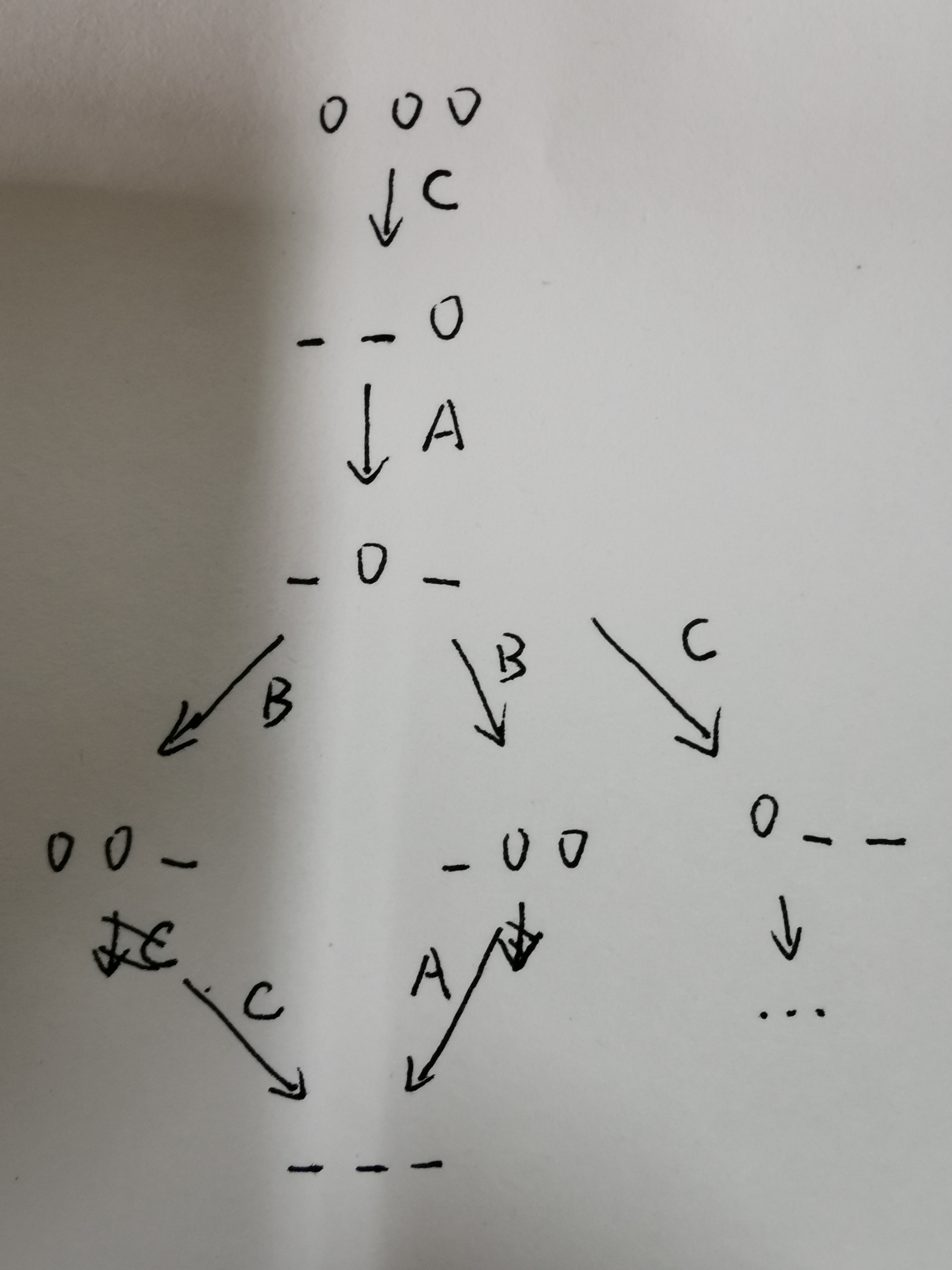
第三题与第二题类似，可以逆推，但前两步可以正推，即第一二步一定是AB
可以得到结果为ABCABA或ABACBA第四题不讲了
第五题
A按钮控制黄绿，B按钮控制红，C按钮控制红绿。
可以看到只有黄色是只由一个按钮控制的（而且其他按钮对格子的前进或后退都是固定的，不会因格子位置的变化而变化），所以必须先让黄色归位，先按7个A，剩下的自然先按C，同样因为C可以控制绿色而B不能。所以结果自然出来了AAAAAAACCBBBBB。其中ABC顺序可以任意更换
第六题可以用方程组（矩阵）的思想
但四个x之和并不是总步骤数，因为四个x转换也要步骤，10步的那个就输在转换步骤太多故最后结果为AAAACAABA
第七题不说了
第八题先观察，在每个颜色的格子未耗尽之前，都是以偶数转移的，而绿颜色需要三个，故我们必须把一个颜色的格子耗完（显然这个颜色是绿色），可以是一次耗完也可以是多次，一次耗完步骤更少，但一次耗完有一个明显的缺陷，就是一个颜色的格子过多。再反过来看，如果要把绿色填满（从零填到六），有多种方法，可以是一次，也可以是多次（无论一次还是多次，最后一个步骤都是两个颜色剩余相同数量的格子并将其移到第三个颜色），根据前面分析的绿颜色数量为零，我们可以在绿颜色格子耗完的过程中让黄红剩余相同数量的格子即三个，这样就不难得出答案:
CCB CCA AAAC
第九题思路差不多，这里不予证明，留给读者当作练习自行完成(￣へ￣)
提示:绿色最少，先耗绿色，填绿色时发现黄色耗完，再填黄色
结果:CCCCB AAAAC CA
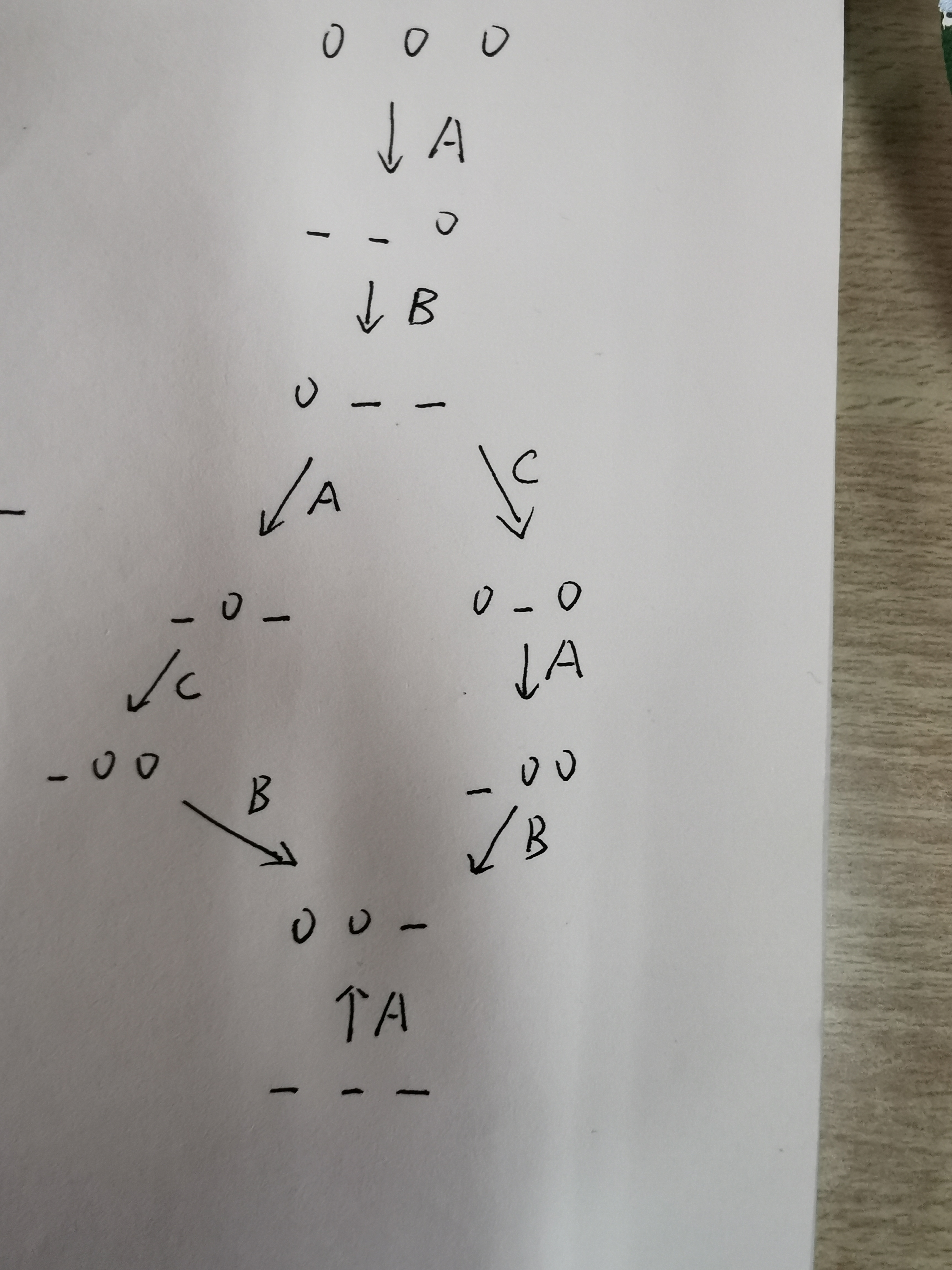
第十题
利用逆推和对称
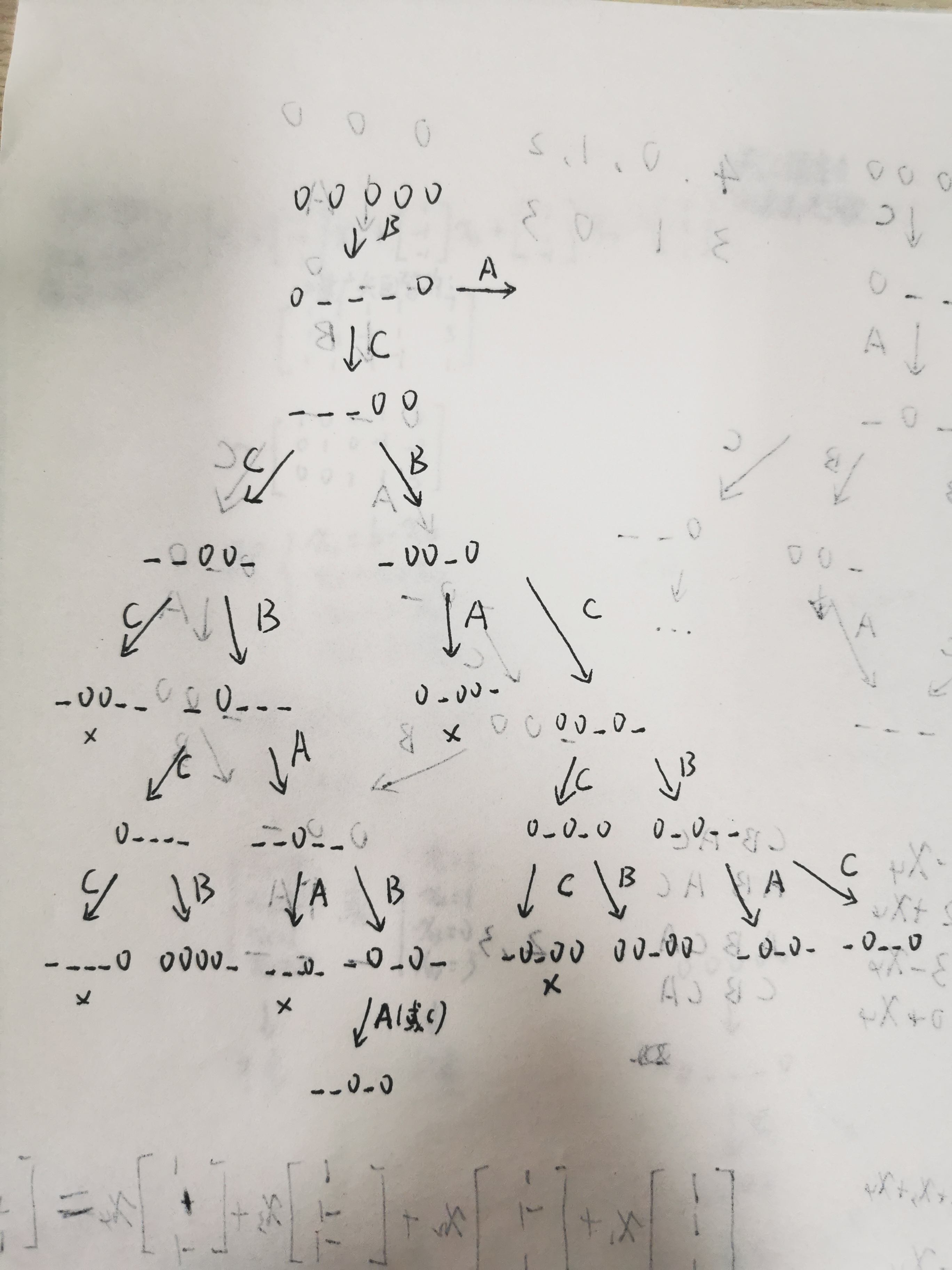打叉的被排除是因为它与它的上面的几个图形重复或对称，这导致这一条支线步骤肯定比被重复的长画到有思路的就可以尝试正推了
经尝试，上图最右面的支路步骤最少
结果为BCBCBCBCB