如果有懒得填/不会填可以直接回复，我刚好一并补充每一关作业。
玩了三天，有所经验和总结，在此分享。欢迎大佬交流更多骚操作。
前置技能：读懂规则。
首先以第六关为例。
首先相当的经典，并没有能够一下就填出来的行或列。但我们可以考虑第一个原则：
「开局找多的填」
很明显这里最后一列，「6,2」是最多的，考虑直接推演这家伙。
但显然是无法直接确定的，如何推演呢？
考虑第一种操作：
「暴力演算，保留合法部分」
这里说的暴力演算并不是指随便找一种可能填，然后去试错，而是列出所有可能，寻找这些可能重叠的部分。
如这个最后一列，「6,2」，一共只有这几种可能：
⚪⚪⚪⚪⚪⚪❌⚪⚪❌
⚪⚪⚪⚪⚪⚪❌❌⚪⚪
❌⚪⚪⚪⚪⚪⚪❌⚪⚪
可以发现，这几种可能中，[2,6]区间必填，第9个必填，所以我们可以直接填上：
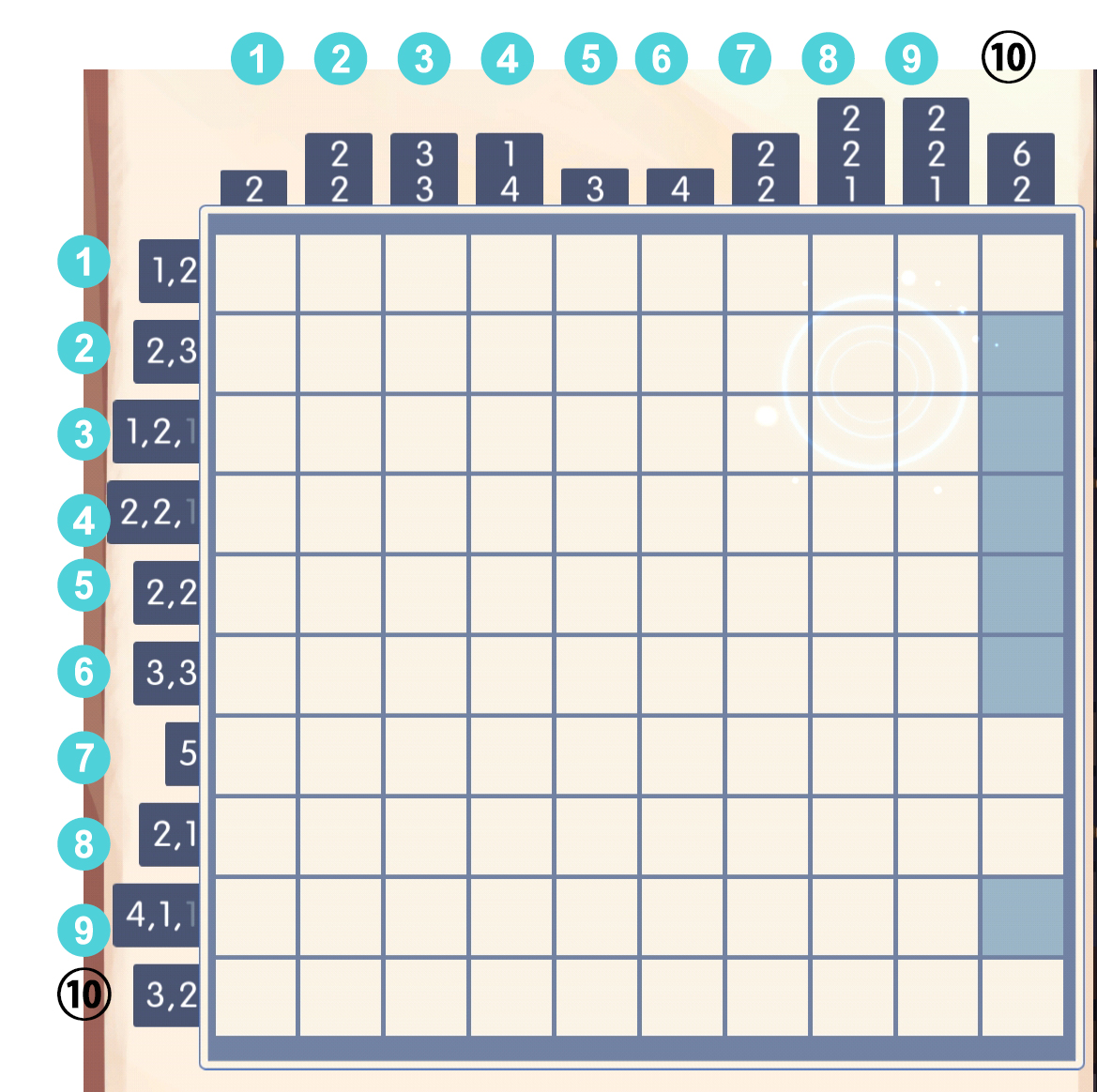这时候根据第[2,6]行（意思是第2行到第6行）的数字，可以直接推理：
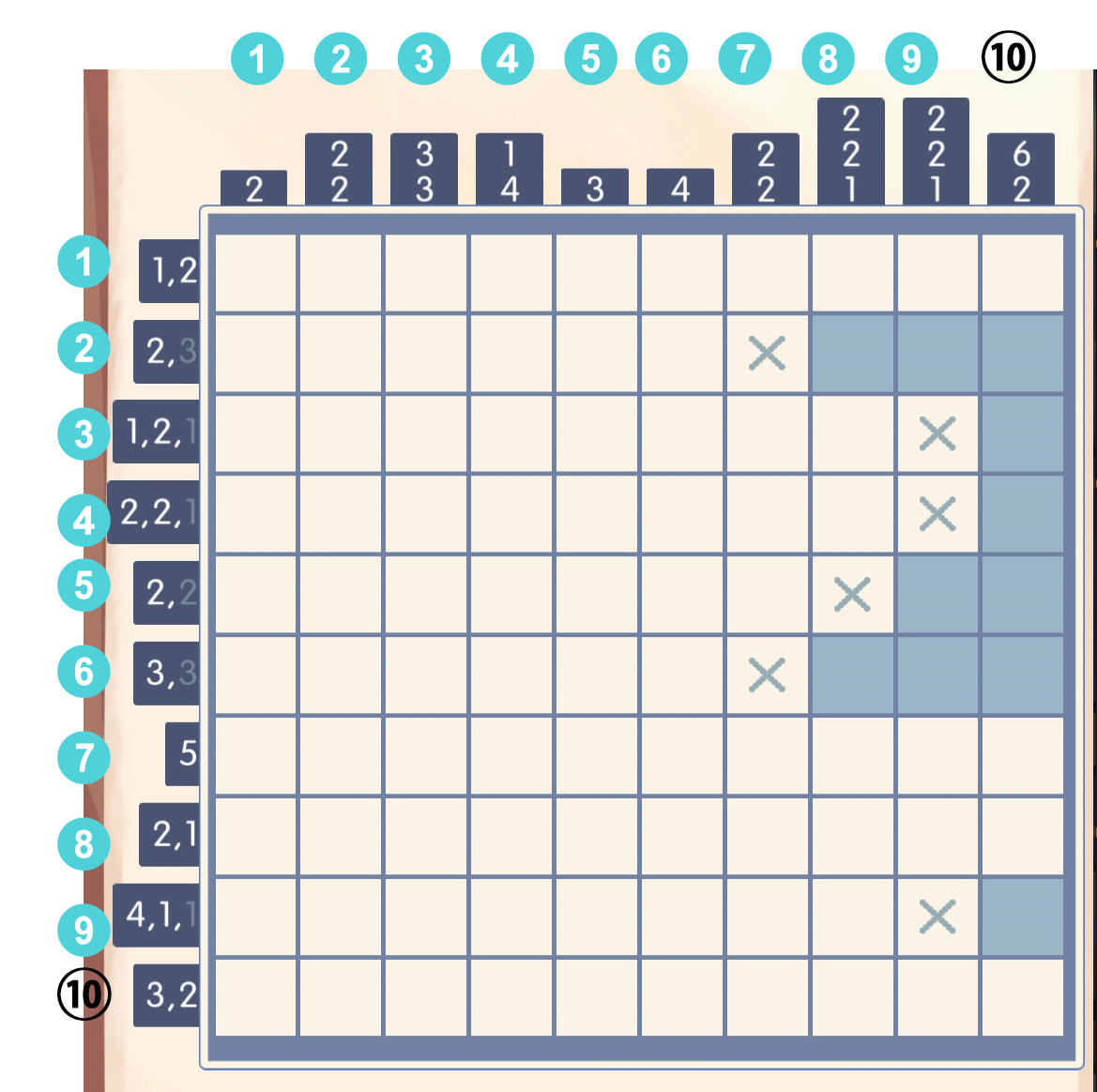观察第九列，很明显第一个必填：
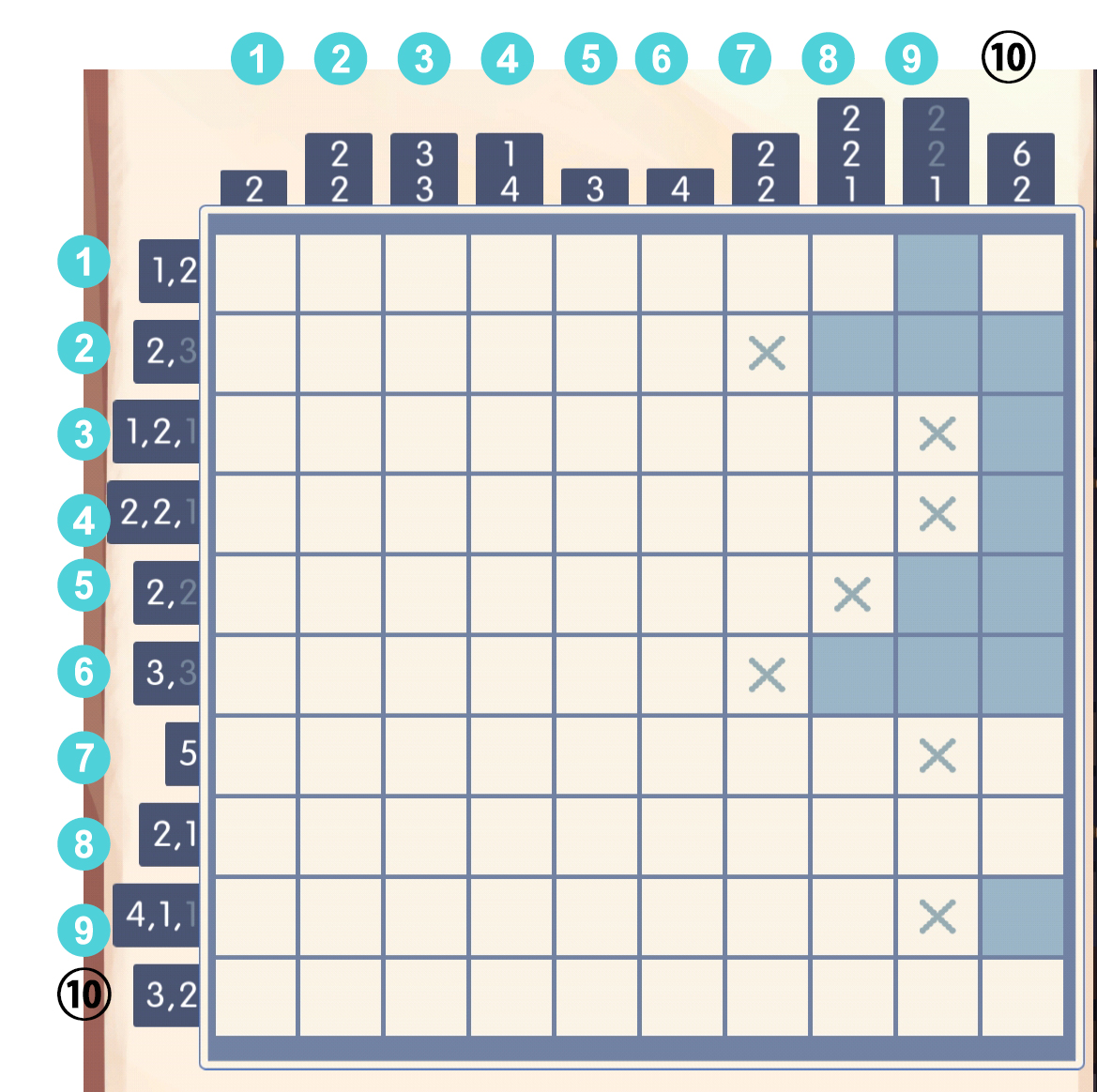再看第八列，需要填2,2,1。一个显然的结论是，2,2不可能填在前4个格子内，所以第二、六行的格子分别与这两个2配对，我们可以直接填[6,7]
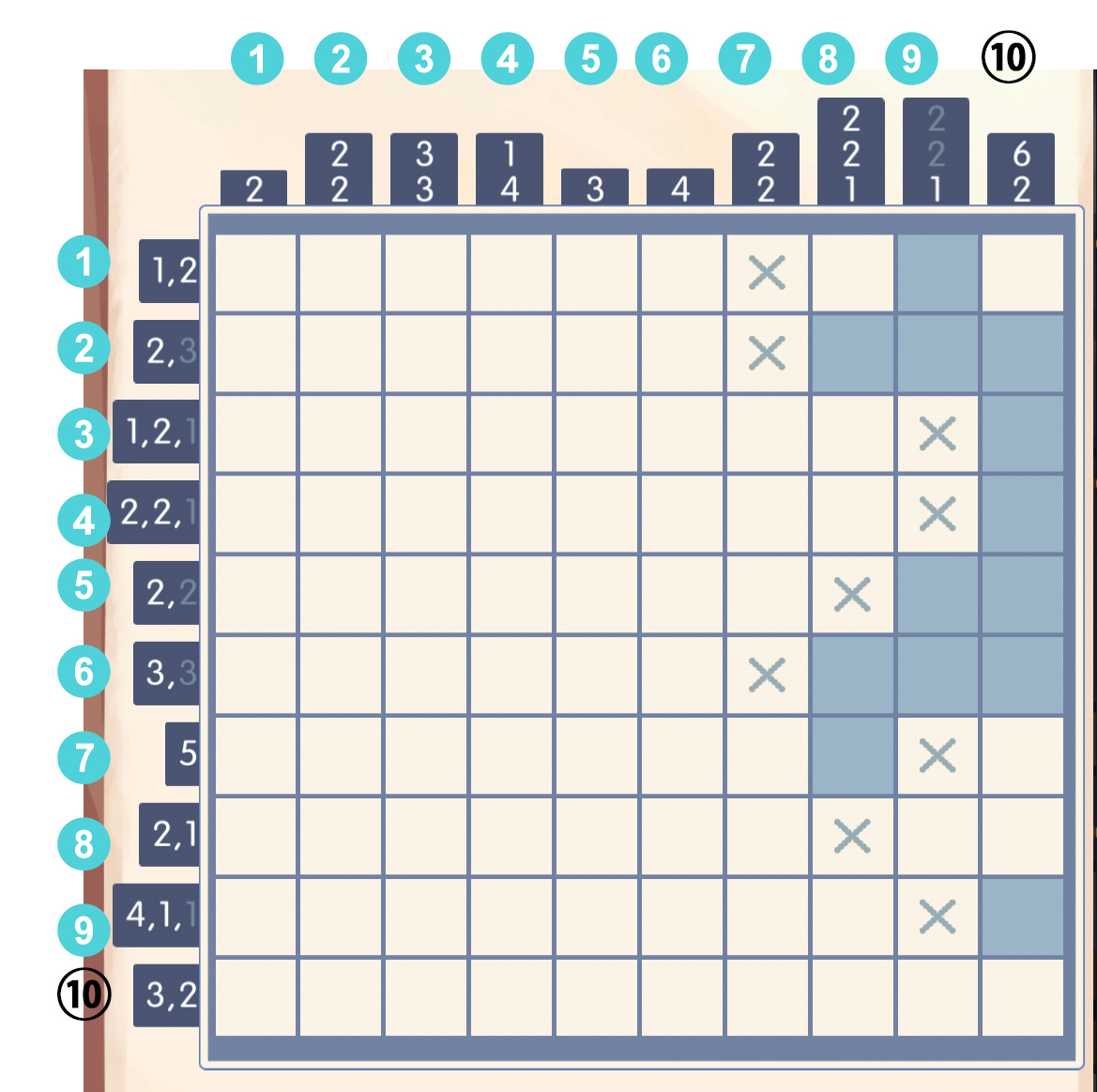于是，这里有个明显的小结论：「如果找到某个格子对应的数字，同时发现这个格子的一边被堵住了，可以直接填出」
发现第七行的格子必然对应的是数字5，同时格子右边被堵住了，可以直接填出：
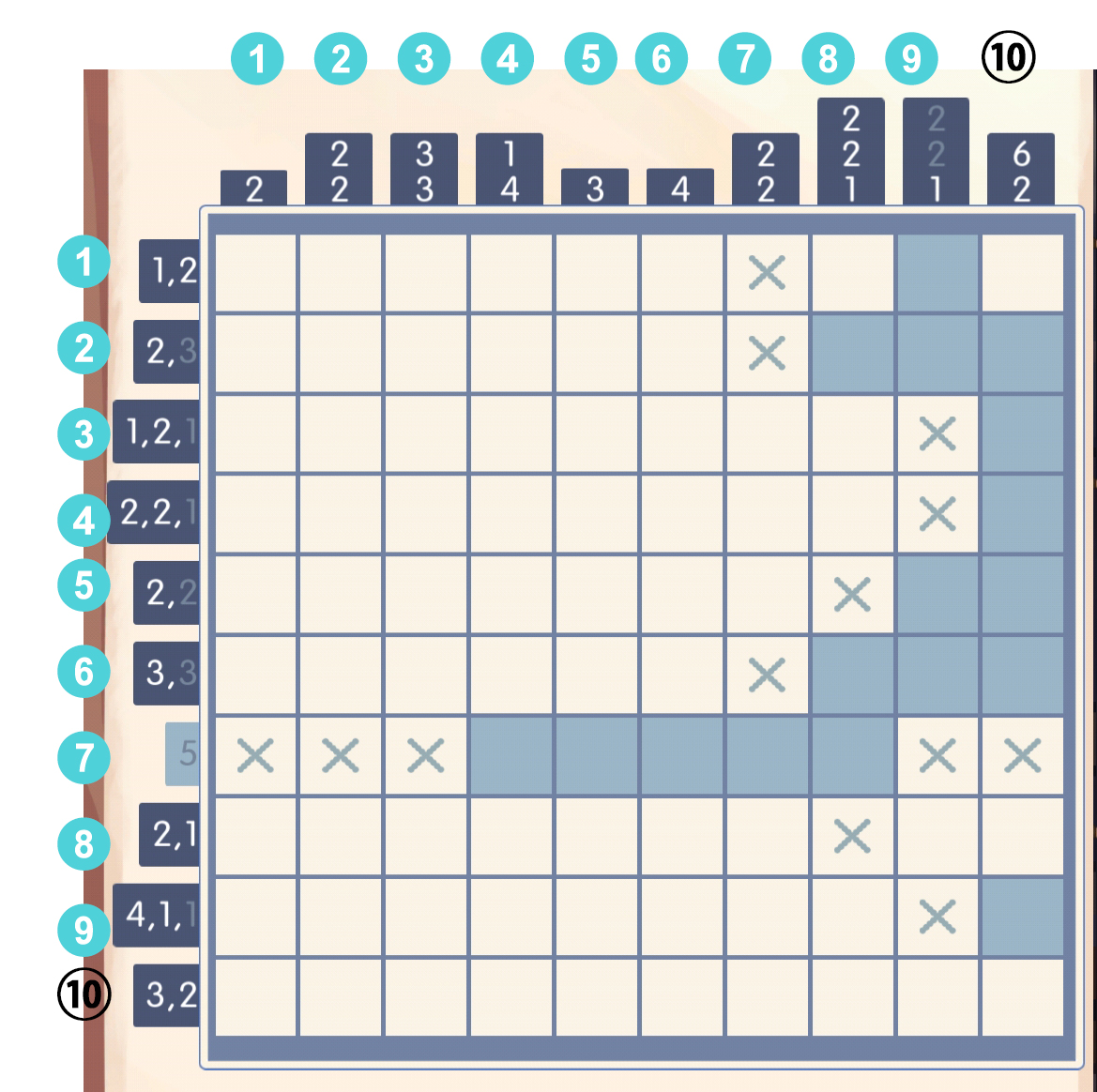于是第七行把最后一列的数字6封住了，6只能往上填：
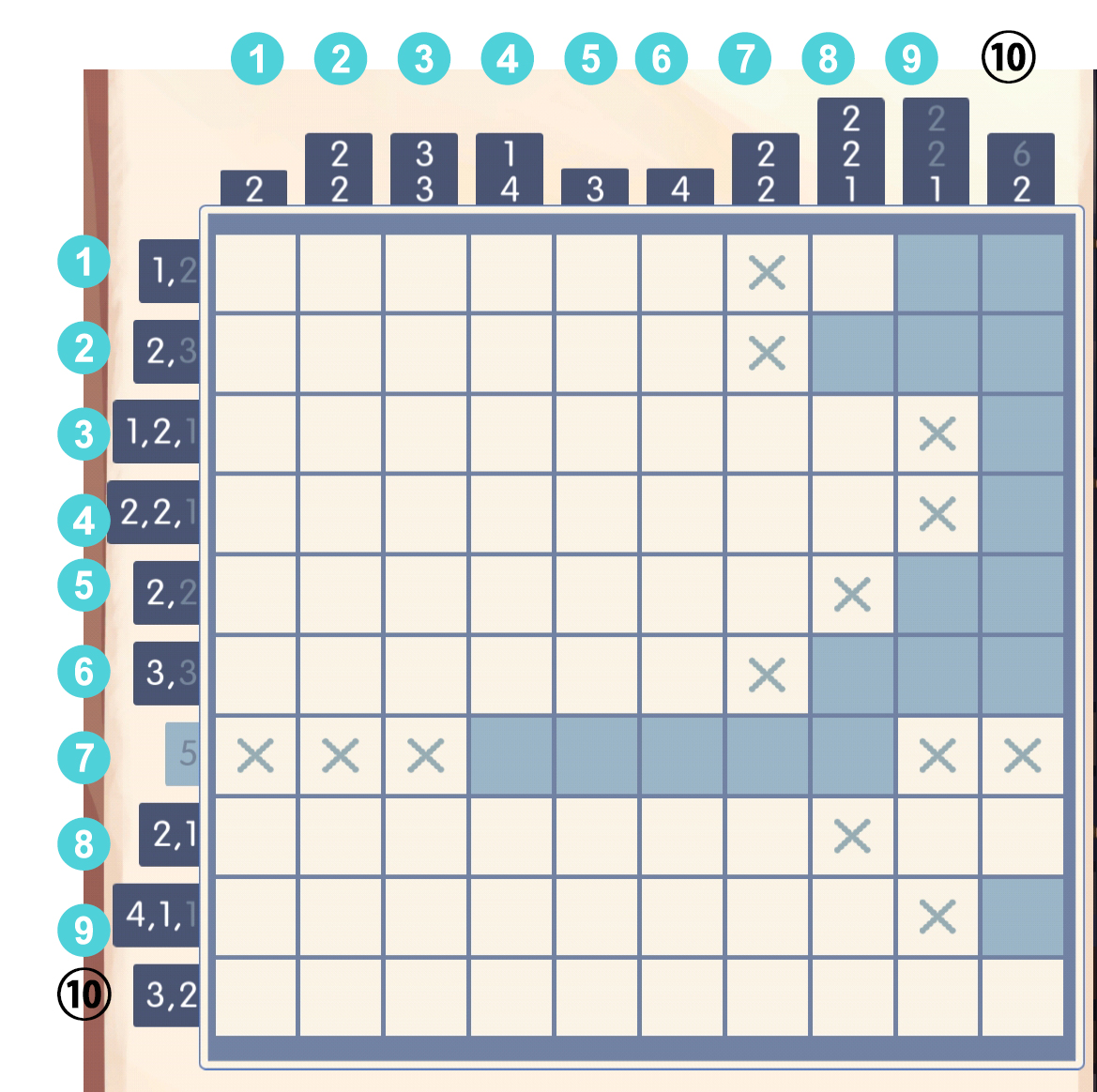填完之后观察第一行，可以把第八列给封上，于是第八列的第一个数字2就呼之欲出了：
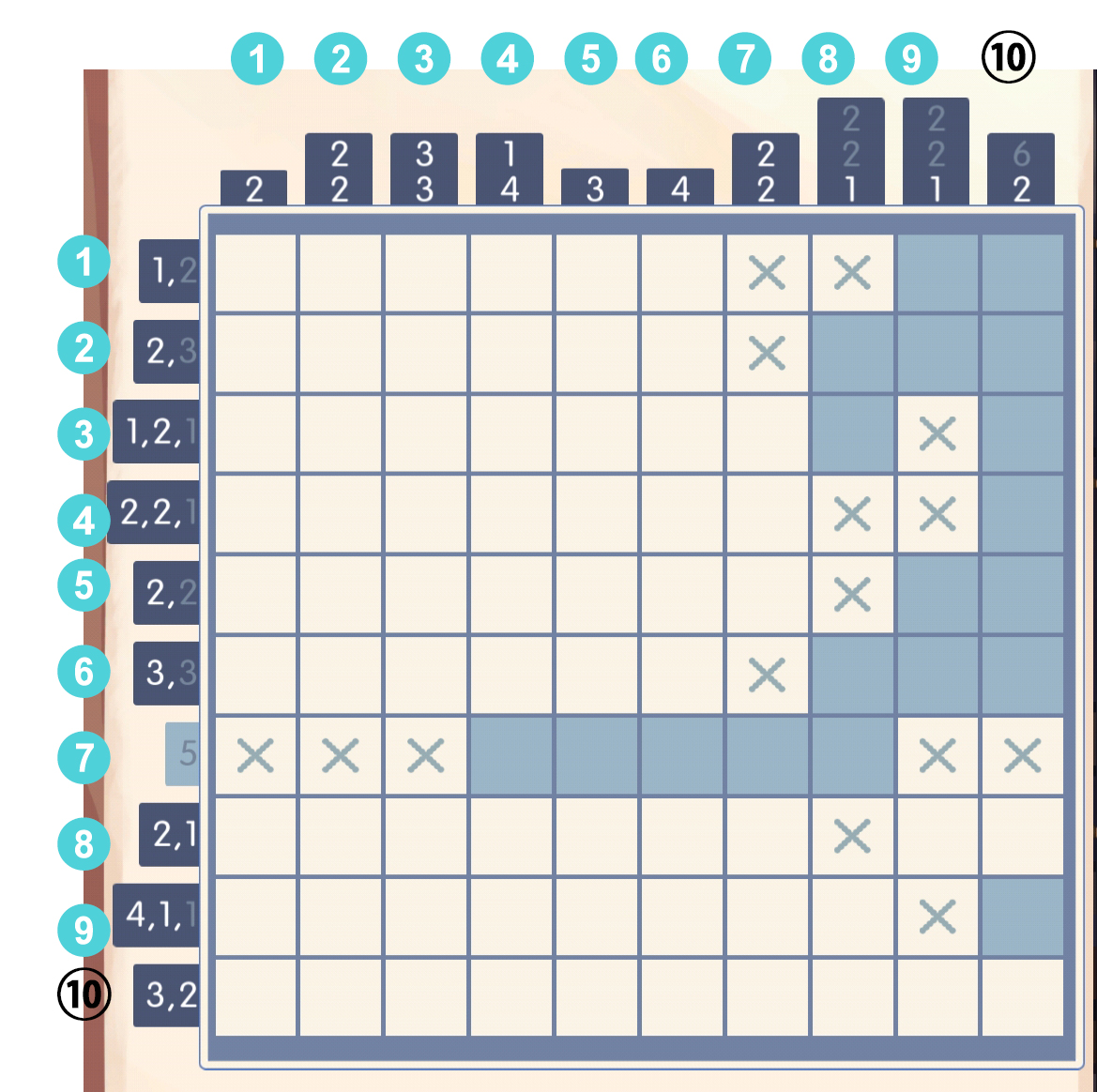刚看完第八列，现在再来推演第七列，一个基本原则：「考虑并存问题，推演数字位置」
发现[7,10]这个区间中，明显不能并存两个数字2，于是一个数字2在上，一个数字2在下。
对于在下的那个数字2，可以直接填[7,8]（堵住了，详见前面的小结论），对于在区间[3,5]的数字2，暴力演算一下[3,4][4,5]两种情况，显然4必填（下面这张图很明显可以把第七列的[9,10]填叉，不知道我当时在想啥）：
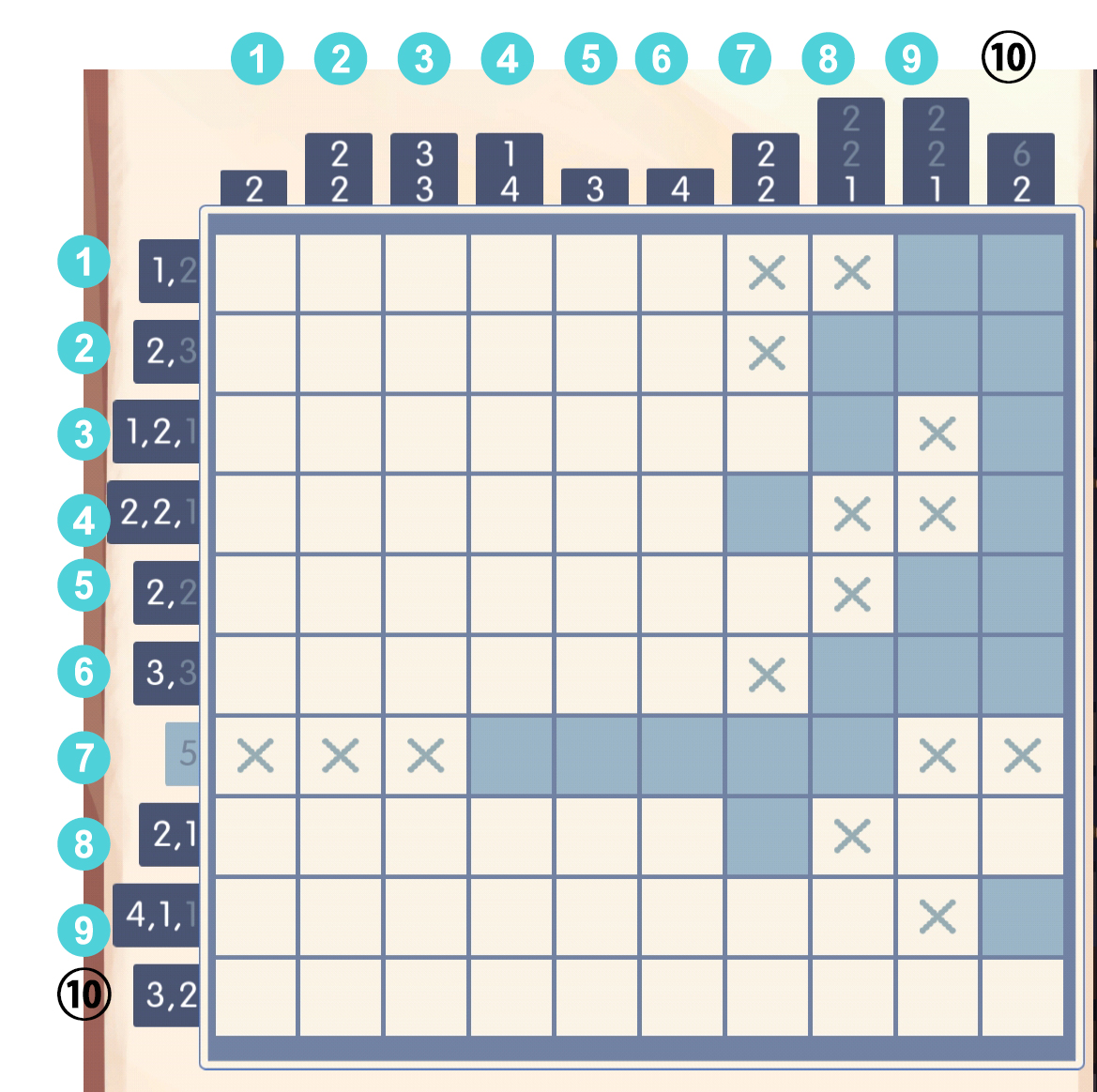把第七列的第四个填出来之后，就可以直接确定第四行的第二个数字2了：
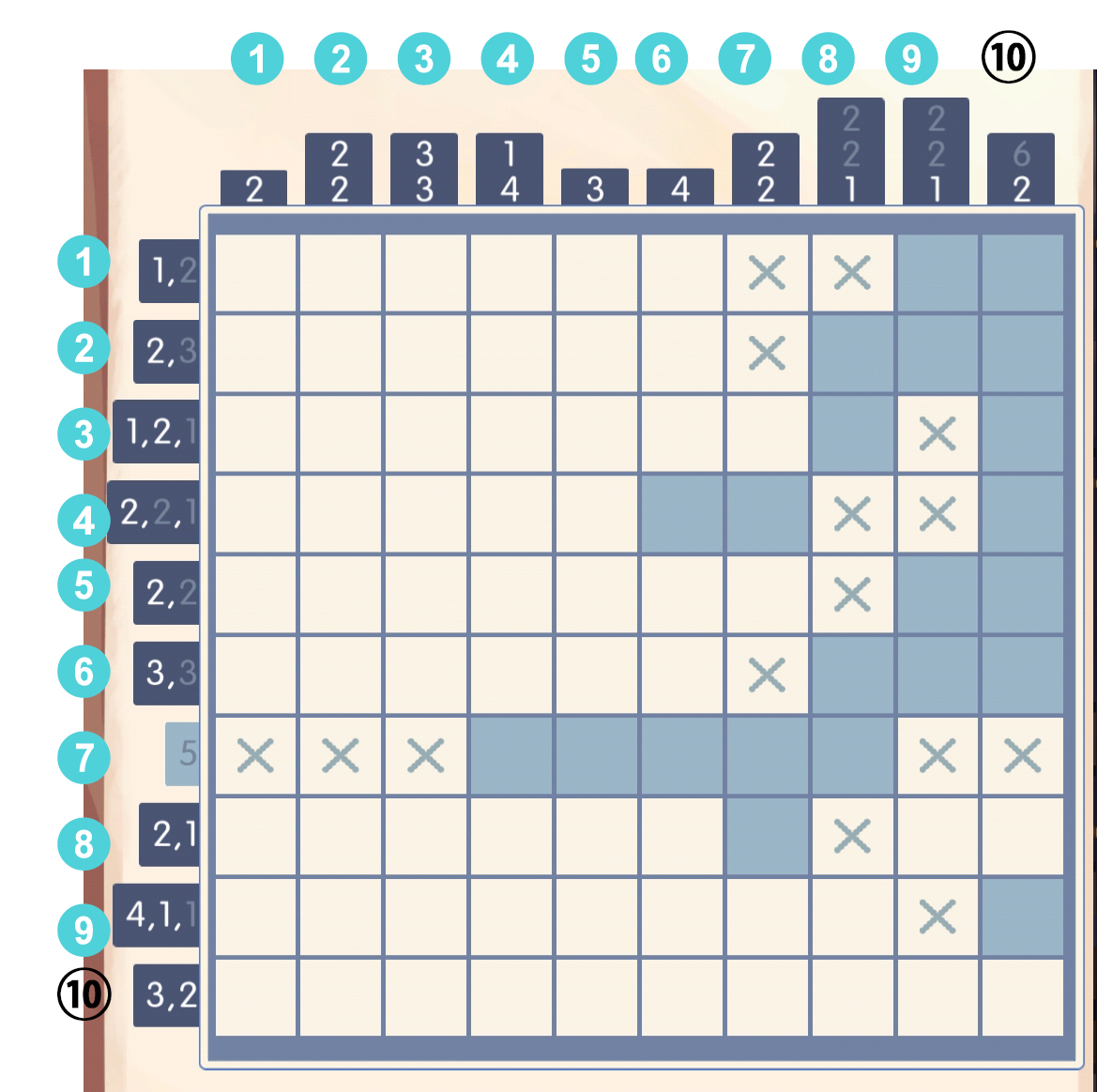于是我们发现，第六列的数字4被[4]和[7]两个方块要挟了，必然填区间[4,7]：
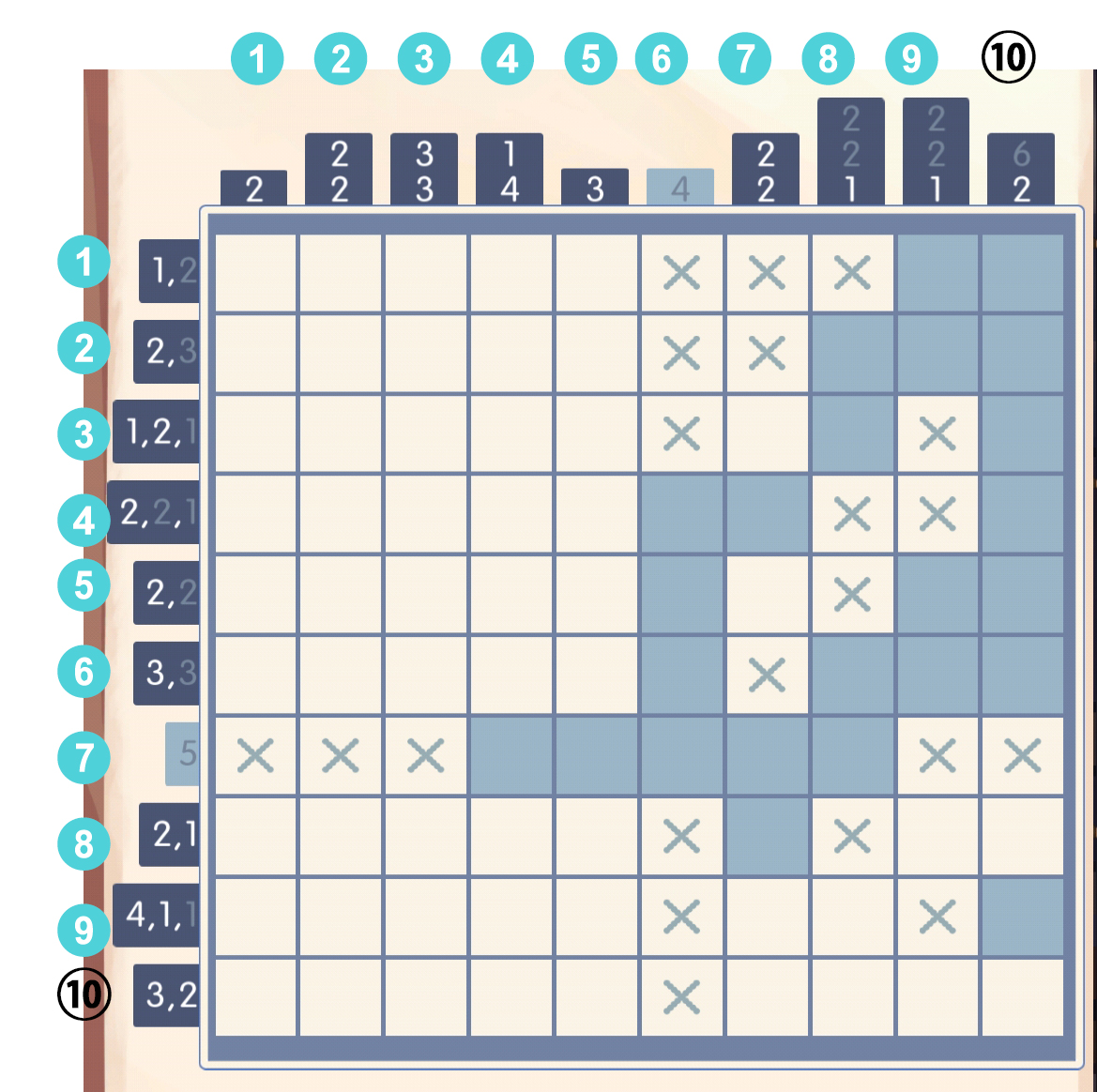这时候，暴力演算一下第十行，显然3,2不能并存于[1,5]，所以[1,5]是3，[8,10]是2（因为上面说过了，第七列的区间[9,10]显然是可以填叉的），演算完后发现，对于第十行，[3]和[8]必填（由于我太蠢了错过了填[8]🤣，说明了填叉帮助推理的重要性！！！）：
于是第三列的第二个数字3对应着这个(10,3)方块，直接填吧：
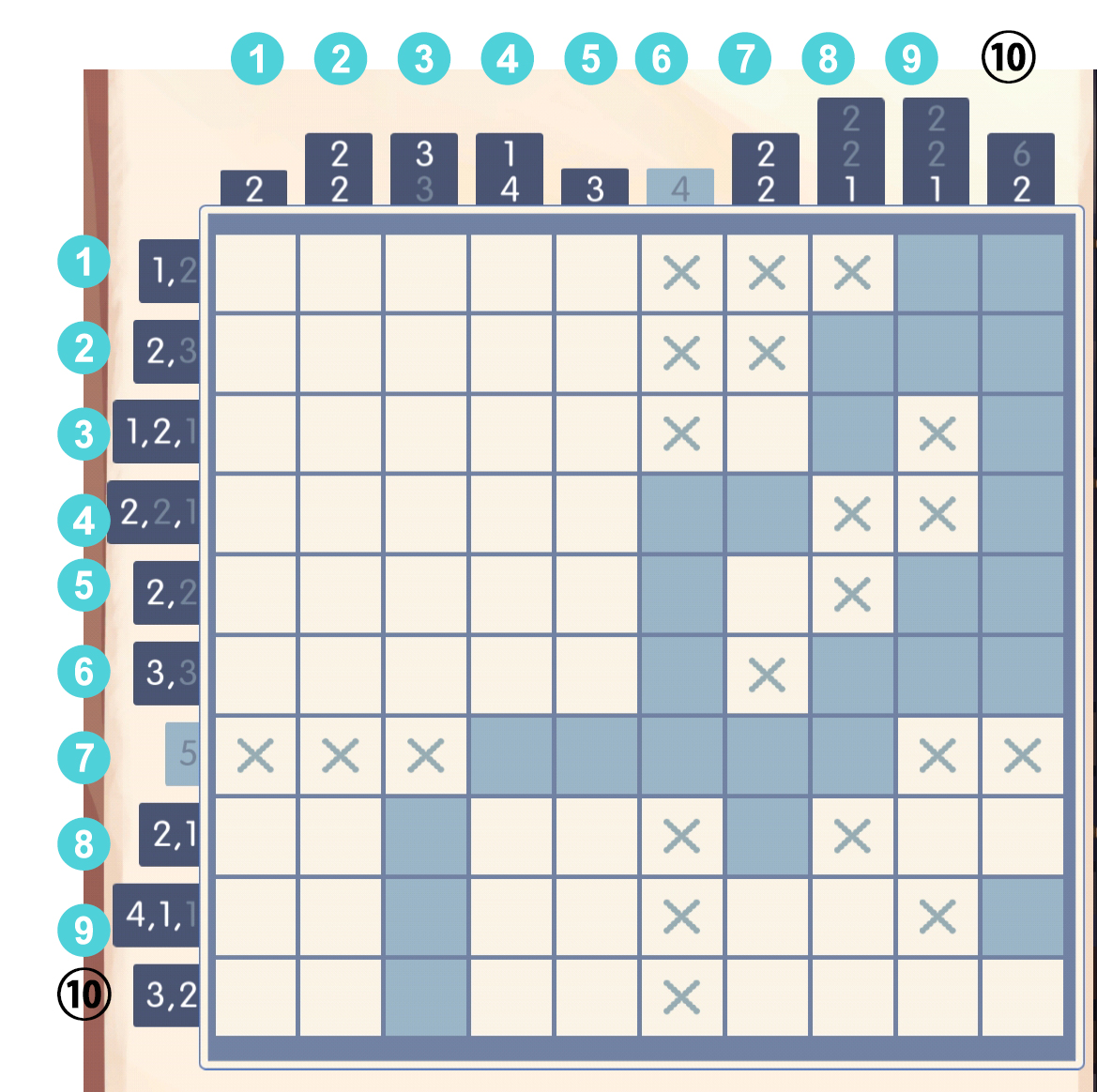于是，对于第8行，区间[9,10]必填叉，
对于第9行，4,1必然不能共存于[1,5]，所以4在[1,5]，1在[7,8]，暴力演算[1,5]，发现[2,4]必填：
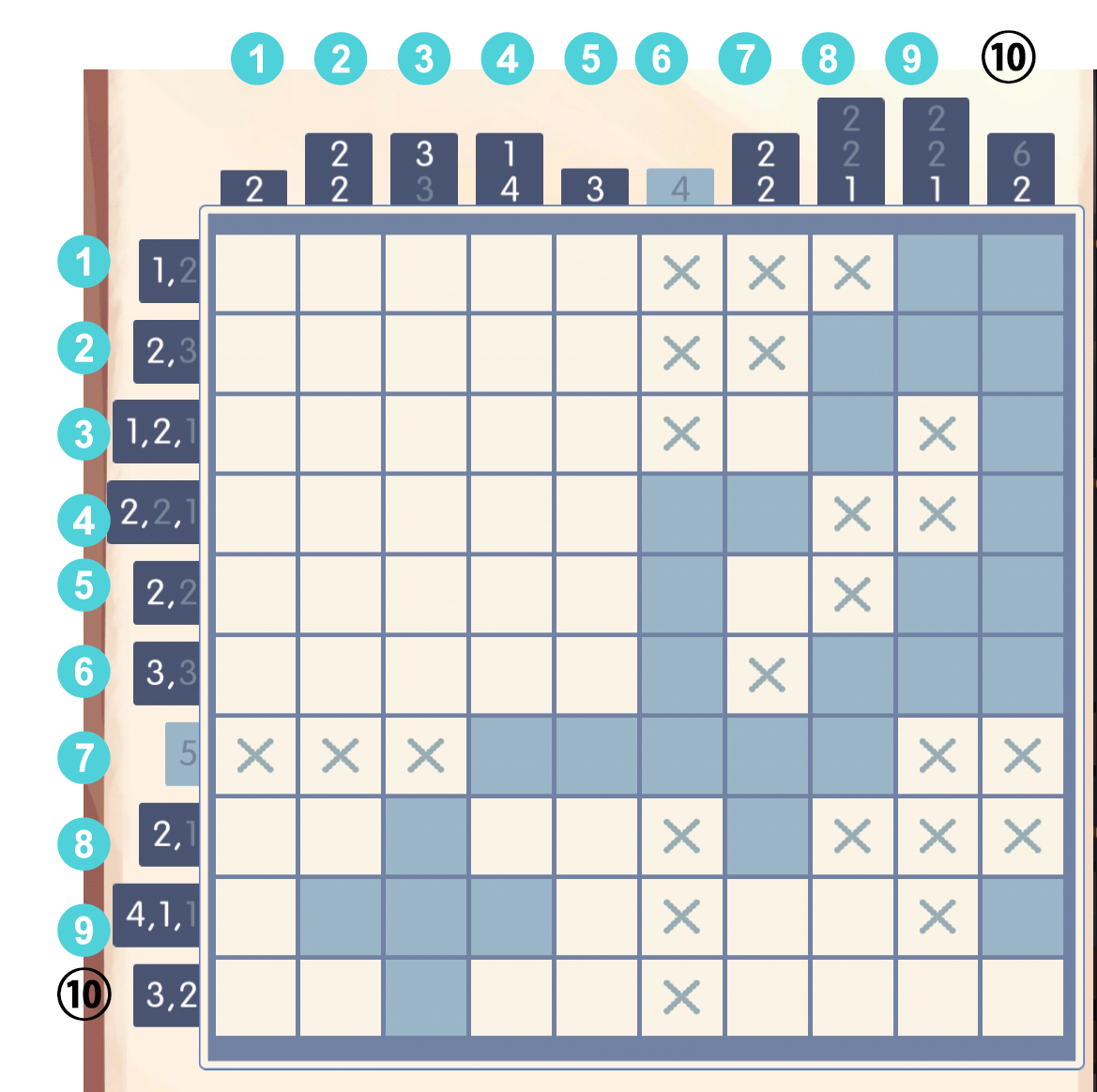考虑演算第4列，于是有一个小trick：「反证法」
如果[7]对应数字1，那么[9,10]显然不能对应4，于是[7]必然对应数字4，那么[7]和[9]就把4要挟住了，暴力演算一下，要么填[7,10]要么填[6,9]，显然[7,9]必填：
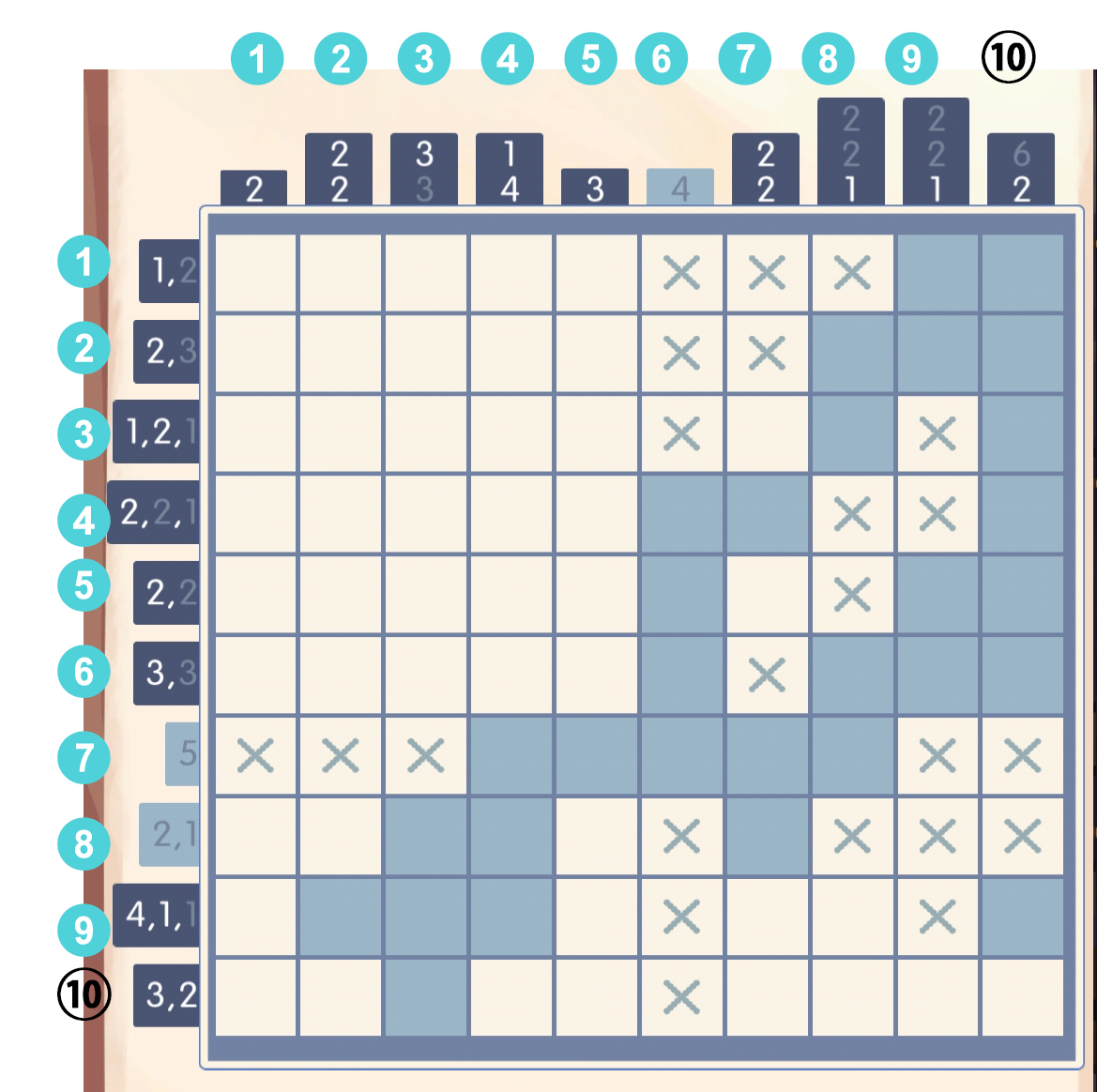于是第八行可以全填叉了。此时发现对于第5列，[7]处的方格被堵住了，而且它显然对应数字3，第十列的[9]也被堵住了，于是有如下情况：
然后第十行的数字2显然可以填了，第五行也应该打叉：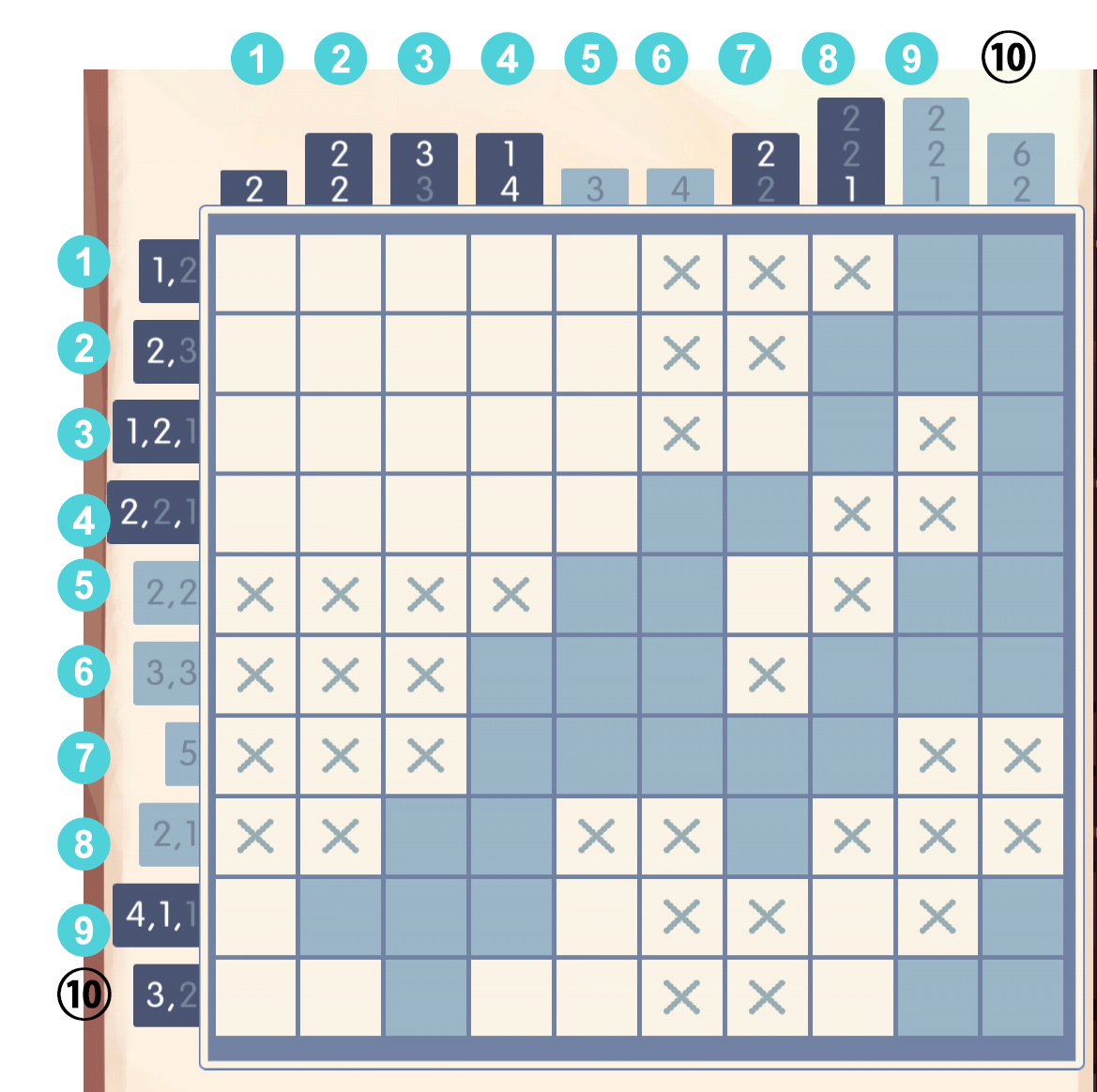
第十行的[8]显然是叉，于是八列的最后一个1就可以填了：
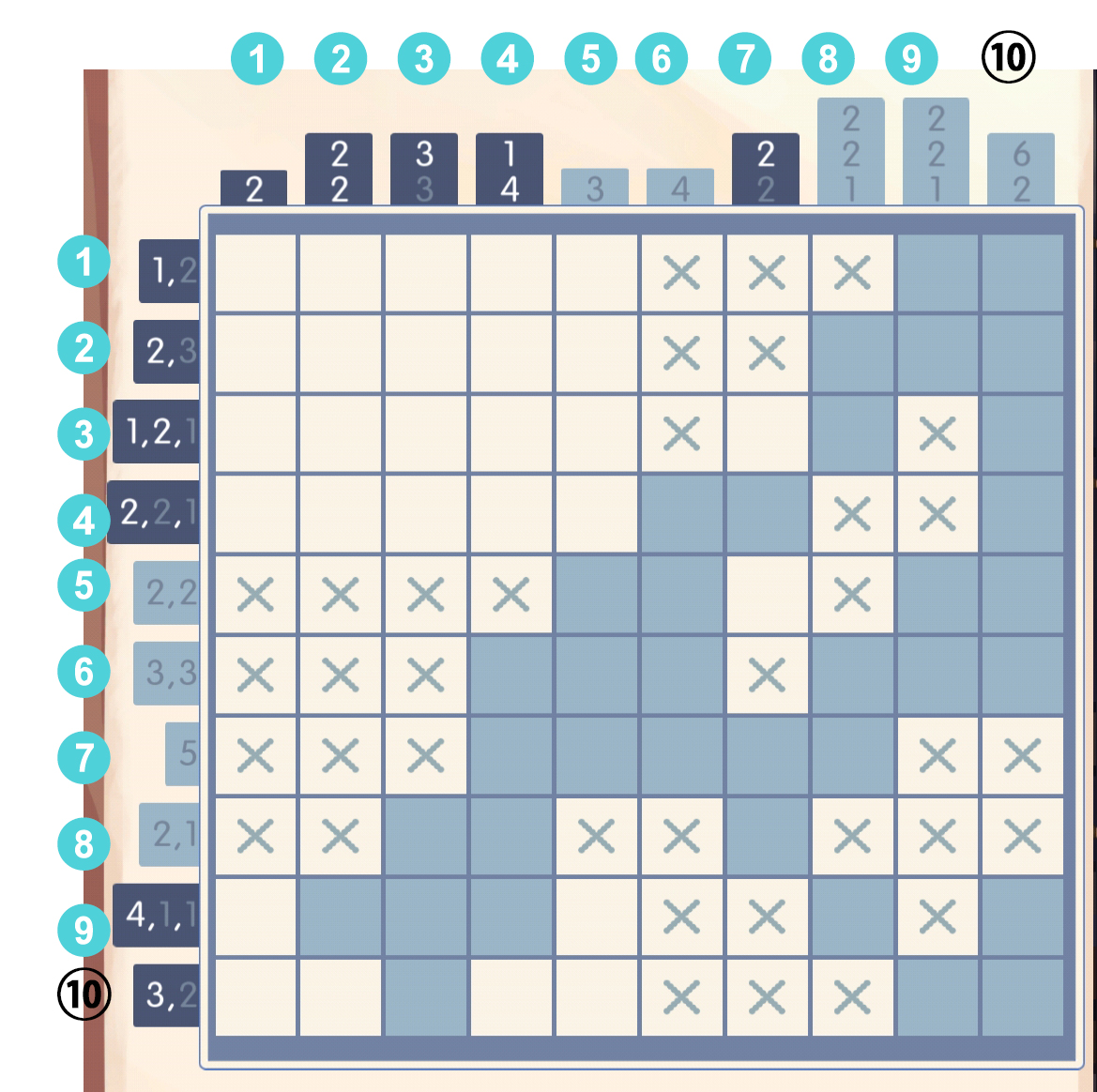于是填一下第七列的第一个数字2：
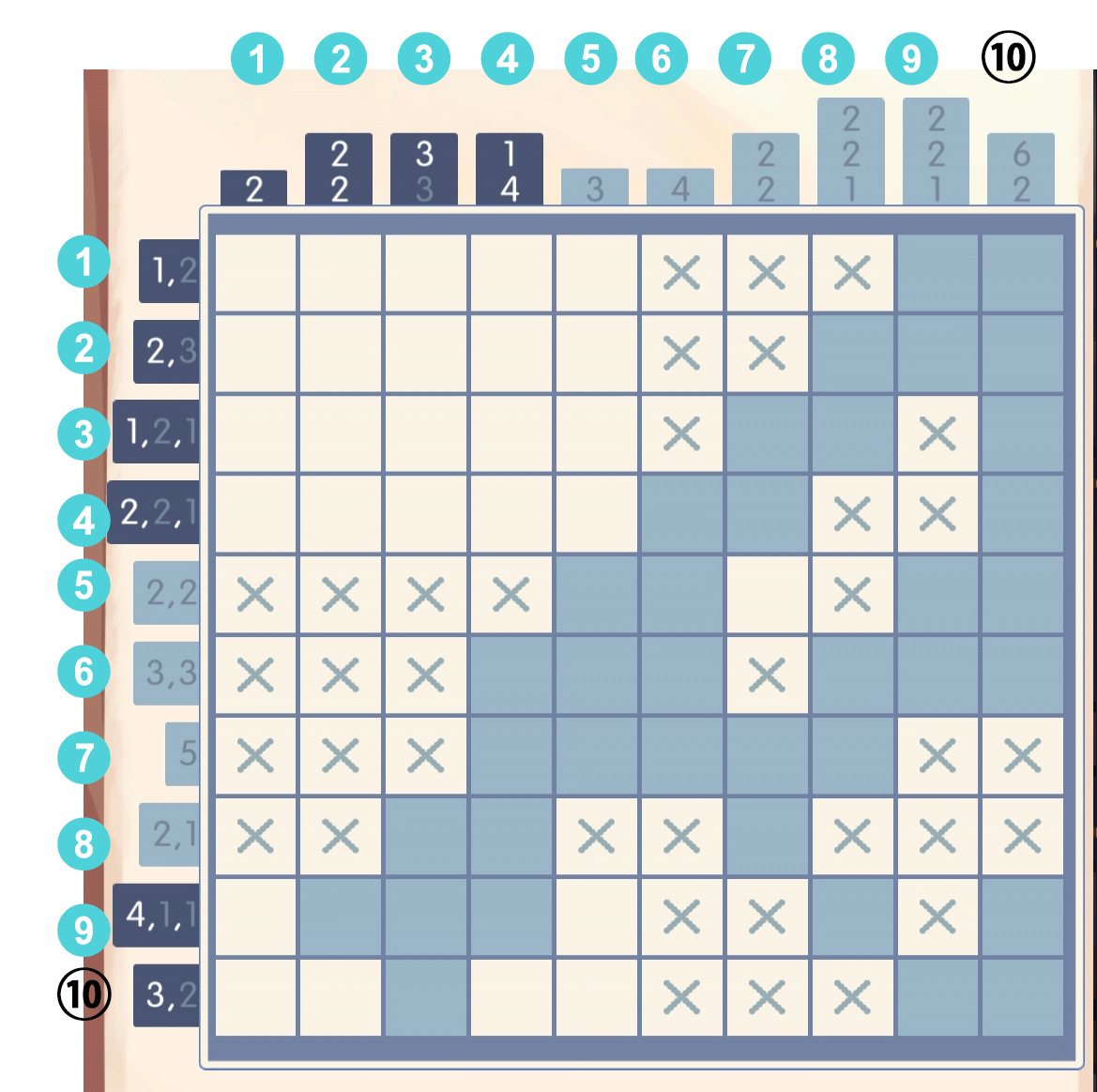打上叉叉：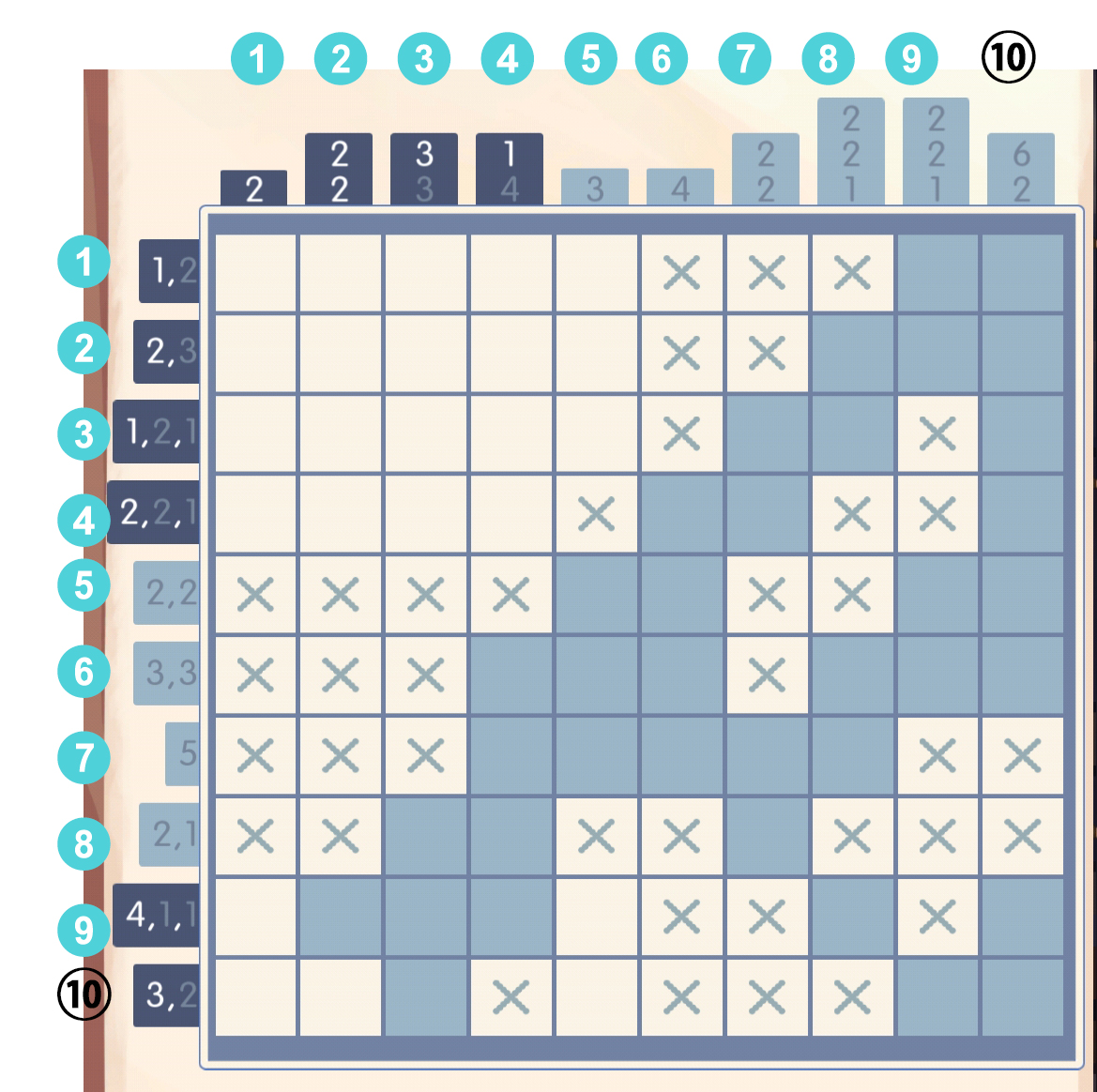
于是第十行和第九行都可以填了，填完后意外地发现第一列已经满了：
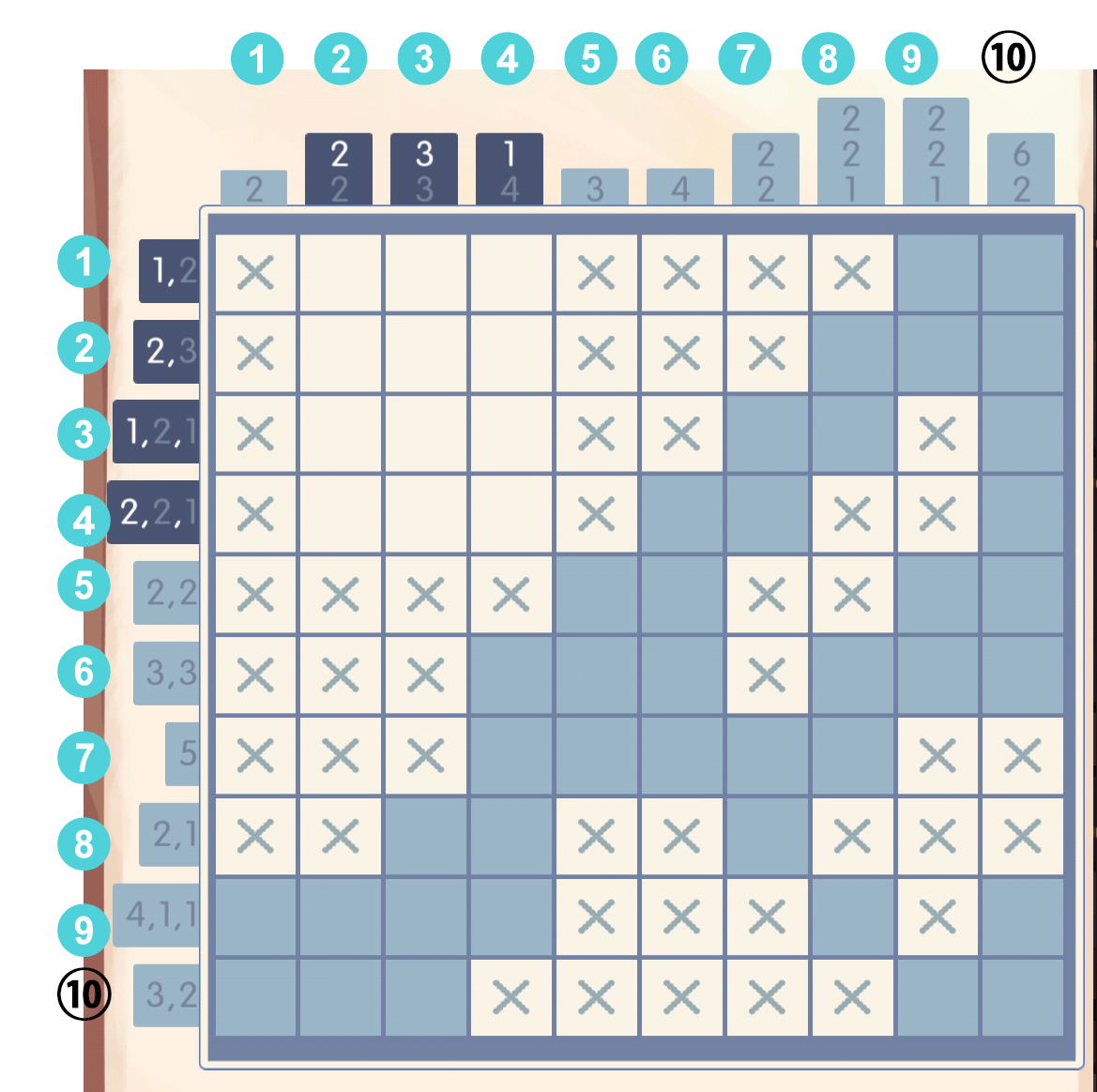先找一个突破口，暴力演算第四行，显然[3]必填：
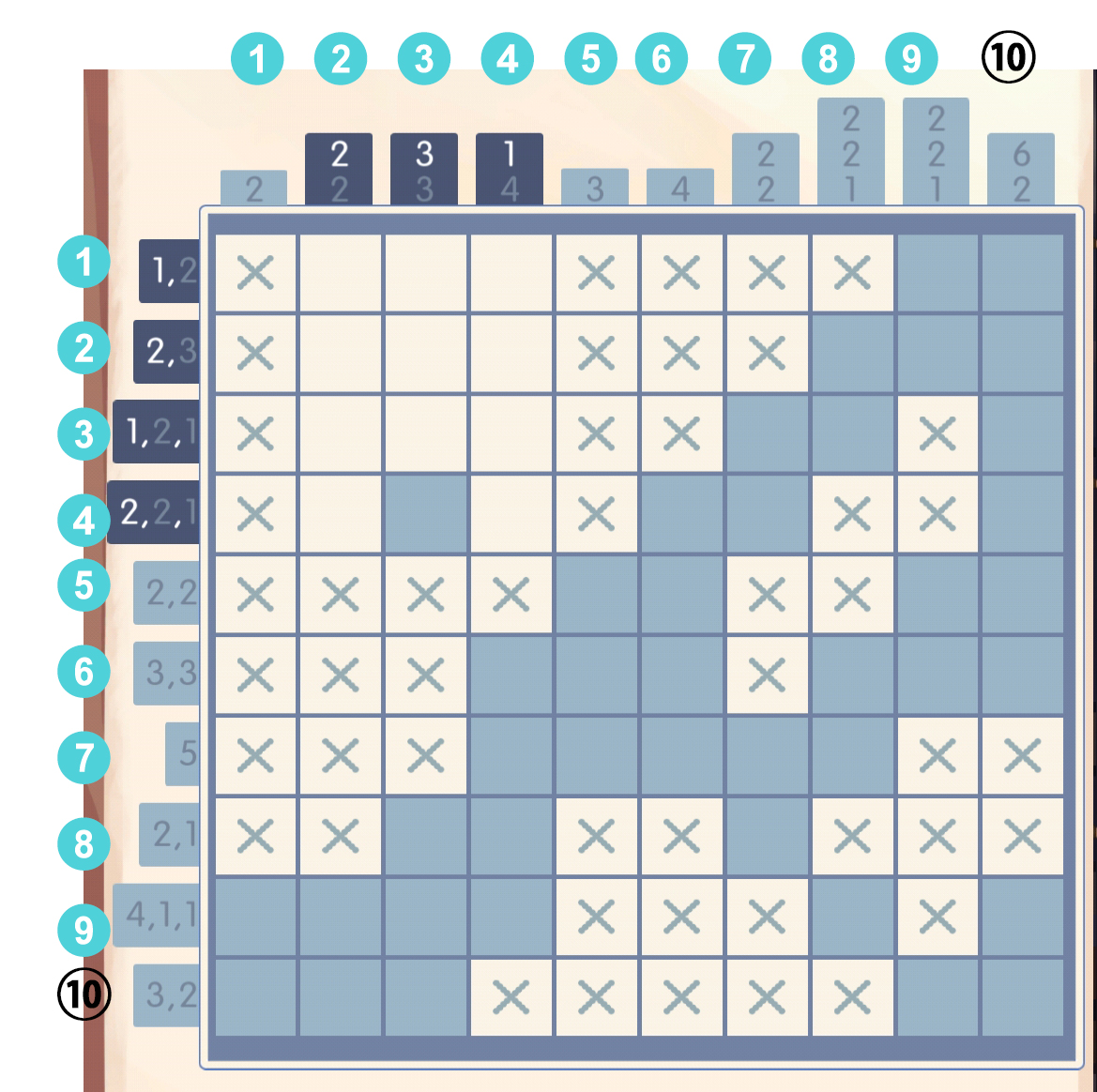于是根据第三列的数字3，可以直接弄出来，此时第三行意外填满：
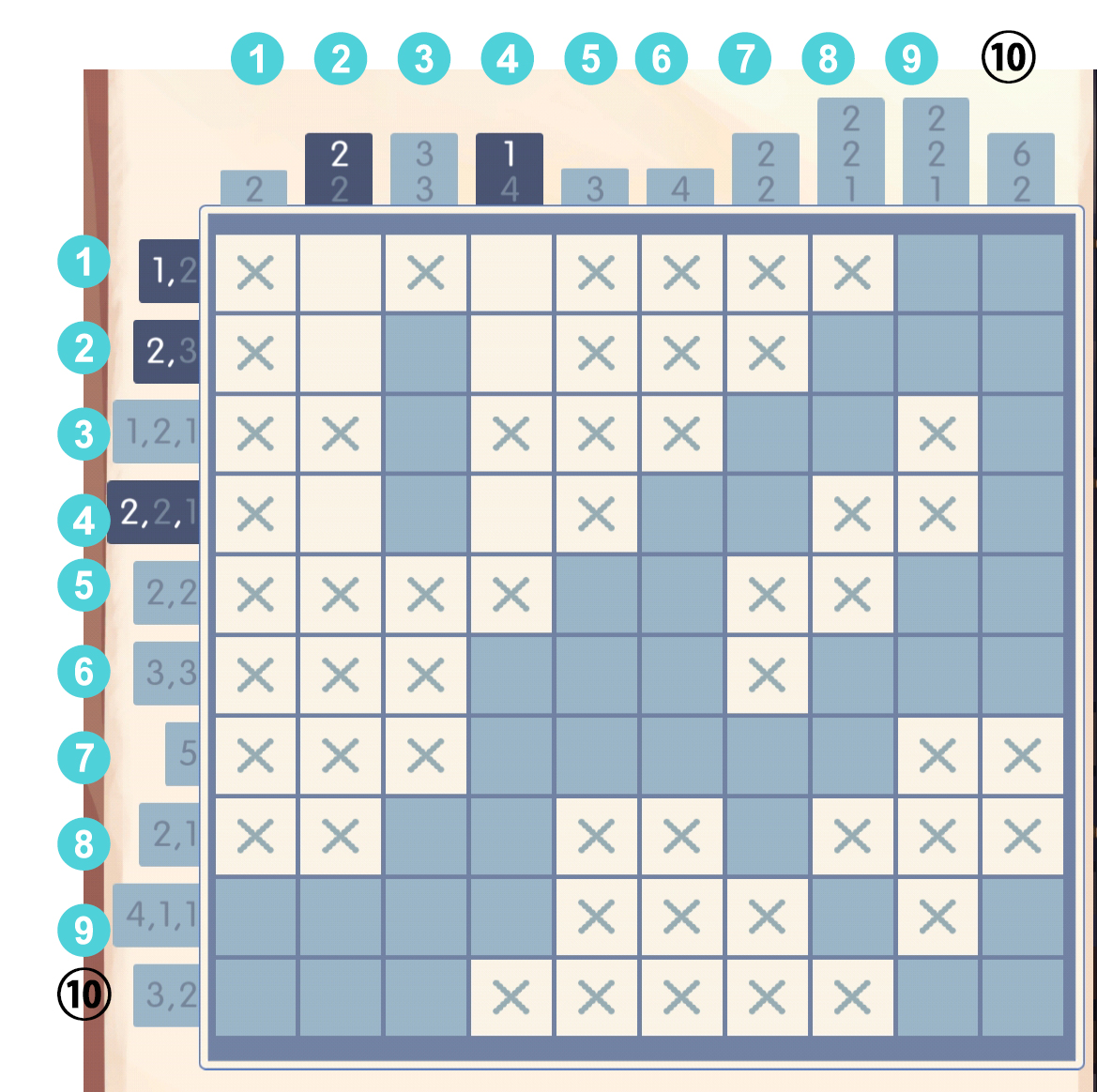第二列不用说也知道了：
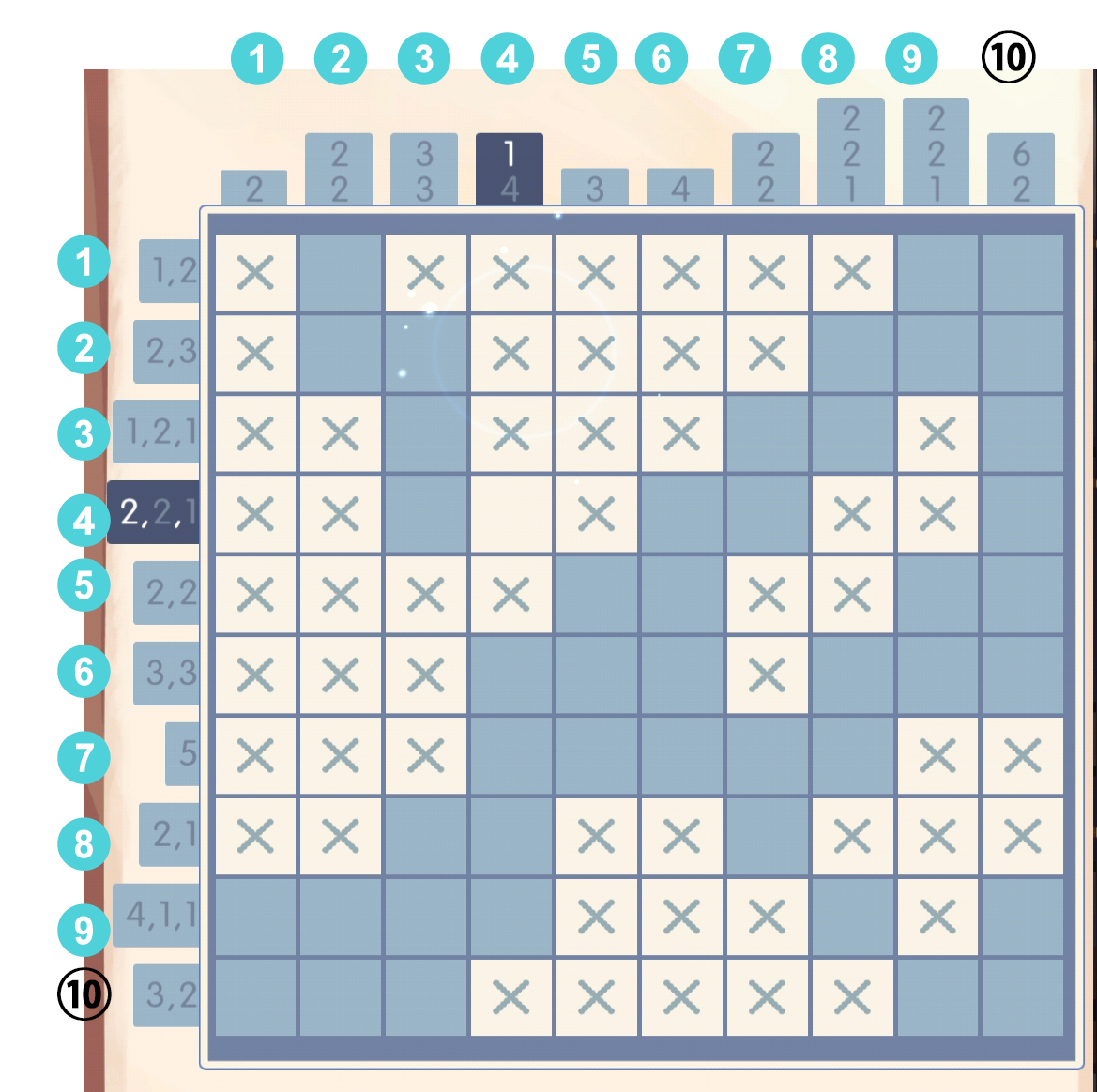最后剩一个，诶，我就不填最后，总结一下知识点！！
一大原则：「开局找多的填」
三大操作：「暴力演算，保留合法（相同）部分」「考虑并存问题，推演数字所在区间」「反证法」
小学二年级就学过：「如果找到某个格子对应的数字，同时发现这个格子的一边被堵住了，可以直接填出」