引
“咚咚咚。”
“门外是谁?”
“原来白羊在家啊!叫了半天也没人答应,我还以为白羊不在家呢。”
忽然想到什么,齐夏浑身一震。一阵细小的滴答声在耳边陡然响起,整个人汗毛竖立。眼前景象如雨滴落入水面般荡起涟漪,变得支离破碎。
……
“门外不是我”
序
"There are two ways of doing calculations in theoretical physics.
One way, and this is the way I prefer, is to have a clear physical picture of the process you are calculating.
The other way is to have a precise and self-consistent mathematical formalism.
...
You have neither."
——Enrico Fermi
1 概述
水体模拟一直是计算机图形学的热点研究领域之一,也是游戏开发、影视制作等领域必不可少的技术手段。如果VR技术进一步发展想要实现元宇宙的梦想,如何在虚拟世界呈现出像现实世界一般逼真的流体效果更是一个绕不过去的话题。从半衰期(Half-Life, Valve 1998)的纯动画纹理贴图,到侠盗猎车手5(Grand Theft Auto V, Rockstar 2013)的纹理动画加粒子特效,到死亡搁浅(Death Stranding, Kojima Project 2019)的弱交互水面,再到最后生还者:第一部(The Last of Us Part I, Naughty Dog 2022)的强物理交互水体,可以看到水体模拟技术不断进步的一个演化过程。

流体力学研究现实中流体作用和运动规律,计算流体力学希望准确快速地再现实际物理流动。看似与计算机图形学的水体模拟目的相同,但计算流体力学并不涉及图像的渲染和呈现过程,而水体模拟也不需要完全遵循物理规律:对它而言更重要的是让观察者“认为”水足够拟真。二者的交集为流体力学的基础研究方法,即对物理对象或过程进行建模并用数学语言描述。由于不懂计算机图形学,以下主要内容均为交集部分。
浅水方程(Shallow Water Equation)是从流体力学基本方程(组),纳维-斯托克斯方程(Navier-Stokes Equations,下称NS方程)基于若干假设简化得出。圣维南伯爵于1871年提出的圣维南方程就是浅水方程的1维形式,而浅水方程至今仍有重要地位,被广泛应用在海洋河流流动、潮汐、溃坝等众多领域。20世纪80年代左右,人们开始研究使用计算机对自然现象进行建模渲染。到90年代前后,将流体视为大量粒子系统并追踪粒子的拉格朗日法,和将流体视为空间流场的欧拉法相继被引入水体模拟渲染。1990年,Kass与Miller首次提出用浅水方程来模拟水面,在当时获得了不错的效果。

本文主要介绍浅水方程的物理过程(虽然以上举例的游戏中未必在使用浅水方程),而不涉及计算机图形学水体模拟部分的光照计算、光栅化等渲染过程。先介绍流体静力平衡假设,再引入边界条件,最后分别用微分法和积分法推导2维浅水方程。此前,先给出NS方程的一般形式用于后续计算,众多流体力学、计算流体力学参考书给出了NS方程本身的具体推导过程,不再赘述。
由质量守恒得出的连续性方程:
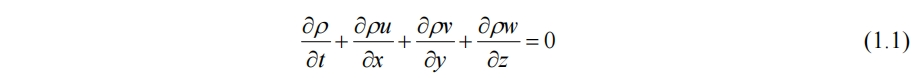
由牛顿第二定律得出的三方向动量方程:

其中考虑了地球自转产生的科氏力的影响。未用矢量或张量表示便于后续对非定常项、对流项等进行分析和变形。动量方程中的科氏力项为
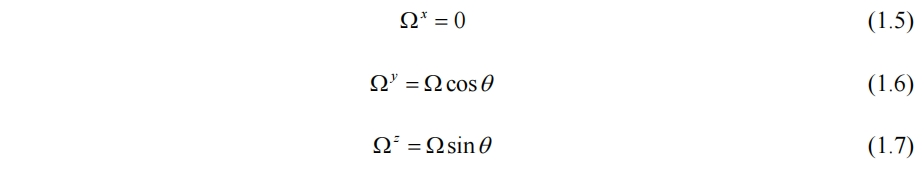
其中θ为当地纬度,Ω为星球自转角速度。当考虑与星球半径一个数量级的大尺度洋流运动或风暴、气旋运动等,科氏力项通常不可忽略。本文中不考虑这种极大尺度。如质量效应2(Mass Effect 2, BioWare 2010)中在不同星球上采矿时,如果需要模拟海洋或气旋流动(当然可能直接做个动画贴图更省事还节省性能开销)。看评价褒贬不一还没入星空(Starfield, Bethesda 2023),不知道里面是否需要模拟行星级别的流动。

粘性力中,切应力项由广义牛顿内摩擦定律给出:

正应力项由斯托克斯假设给出(ii非哑标)

2 基本假设
2.1 流体密度不变
与气体相比,固体和液体的可压缩性要小得多,在温度没有剧烈变化的情况下通常可视为恒密度。对于海洋等研究对象,其含盐量、温度、含沙量等会对密度造成一定影响,但暂时不考虑,也认为具有恒定的密度。在2.6.3节中有布辛尼斯克(Boussinesq)假设供修正。在密度为常数的情况下,(1.1)~(1.4)式的密度可以提到括号外。(1.1)式退化成
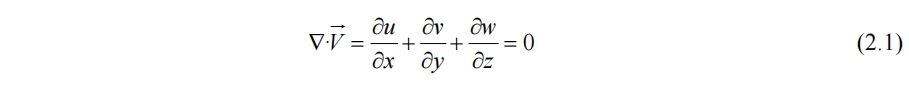
2.2 切平面近似
在流体尺度与地球尺度相比较小的情况下,流体在地球表面上的运动可看作是在与地球接触处的切平面上的运动。此时对切平面上物体的运动而言,起主导作用的是垂直于运动平面方向的Ωz,而忽略Ωy。
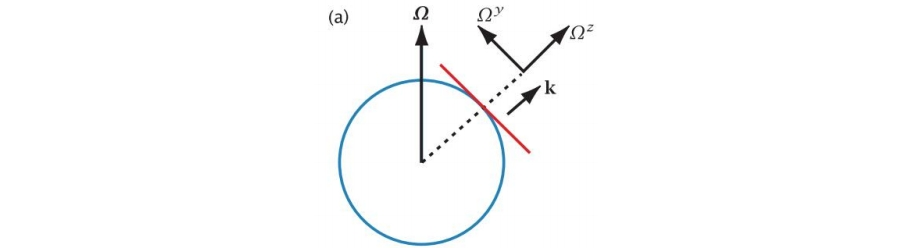
2.3 浅水近似
浅水方程要求流体深度(z)方向尺度远小于长度和宽度(x-y)方向尺度,具体原因见2.7节。
2.4 平面高度函数假设
认为水面与水底的高度可表示为x y t的函数。见(3.1)和(3.2)式。
2.5 拉格朗日假设
拉格朗日假设流体微元一旦进入水面或水底,将永远保持在该曲面上。
2.6 流体静力平衡近似
流体静力平衡近似认为流体在竖直方向的加速度可以忽略不计。从最简单的角度看,在(1.4)式中忽略科氏力、粘性力,等式左边为z方向的加速度Dw/Dt,右边只剩压力项和浮力项。当竖直方向的加速度与重力相比很小时,Dw/Dt≈0,所以在静力平衡状态下流体的压力梯度与浮力项平衡。定量分析如下:
2.6.1 量纲分析
考虑z方向动量方程(1.4)式的各项相对大小。有如下特征尺度:x、y方向的长度尺度L,速度尺度U;z方向深度尺度H<<L,速度未知;地球自传角速度尺度Ω,则根据(2.1)式可知w方向速度尺度为
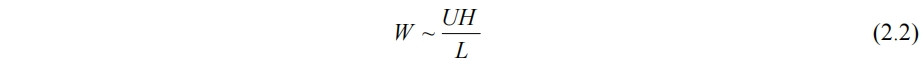
对于(1.4)式中各项,统一除以密度再分析有

如果根据特征速度和特征长度构造特征时间尺度,则
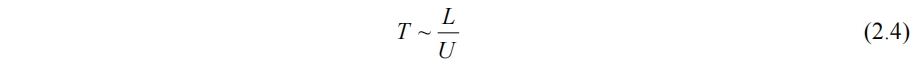
将(2.2)和(2.4)带入(2.3),得到非定常项和对流项相同,正应力和切应力相同。U~L二者一个量级,W很小,非定常项和对流项为小量。地球自转角速度很慢而U不大,科氏力项也非常小。粘性项中由于运动粘度ν在10-3量级远小于H,故正应力项也是小量。所以,只有压力梯度项能够跟浮力项平衡,其他项都可忽略。
如果引入3个无量纲数,分别为惯性力与粘性力之比、与科氏力之比、与压力梯度项之比:
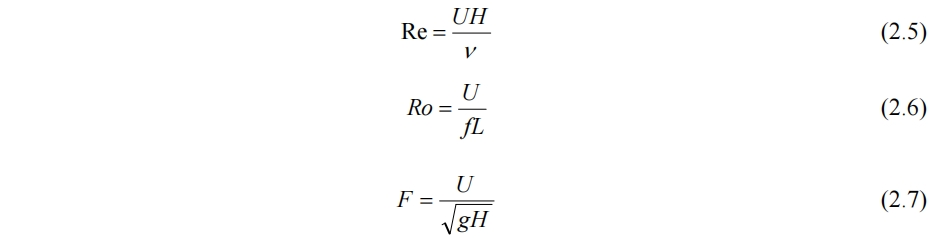
其中f=2Ωsinθ,再用浅水波内的“声速”,即特征信号传递时间(见2.6.4节)当作时间尺度,

对(2.3)各项再除以g,可化为

其中Re数在100~1000量级。Ro数在河流、海岸附近为1左右,研究地球大尺度洋流时Ro在10-3量级(此时不可忽略,文中不考虑)。F数很难超过0.2。各值带入(2.9)也能发现只有压力梯度项能与浮力项相当。
综上,在流体静力平衡的假设下,z方向动量方程(1.4)退化为
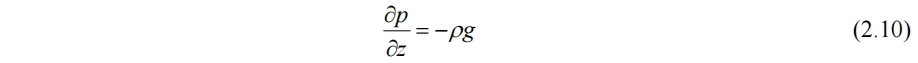
式(2.10)也称静水压平衡方程或欧拉静平衡方程。如果将水压分为两部分

其中p'为修正压力,而ph有
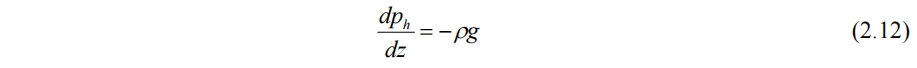
带入无粘无科氏力的动量方程得
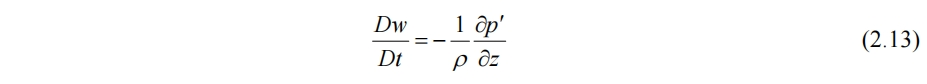
因此对于常密度流体而言,重力加速度等效于对压力分布进行修正,使原动量方程的浮力项消失,而重力本身不会产生动力学效应。
如果认为水面压力ps为常量并取为参考点,ps=0,Zs为水面高度,是x、y、t的函数。积分(2.10)得

2.6.2 水平速度与深度无关
式(2.14)对x求偏导得
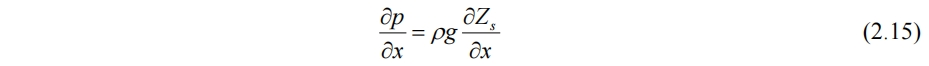
可见(2.15)式与z无关。带入x方向动量方程(1.2),可见x方向加速度与z无关(z方向粘性项通过量纲分析可忽略)。y方向同理。因此u、v与z无关。
2.6.3 布辛尼斯克假设
流体静力近似在很多情况下较为准确,但误差随海水密度变化而增加,尤其是海洋含盐量等有一定变化时。由于整体流体的密度变化量一般要小于百分之几的量级,这样的改变量对于惯性项和粘性项而言几乎没有影响,但对浮力项有较大影响。布辛尼斯克(Boussinesq)提出,在动量方程中,可以认为除了浮力项之外的密度为常数,而浮力项本身的密度会受到其他因素影响。此时密度视为一个常量加变化量
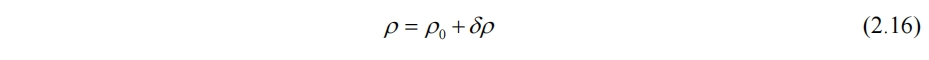
其中ρ0为常量,而变化量δρ<<ρ0。带入z方向动量方程(1.4)
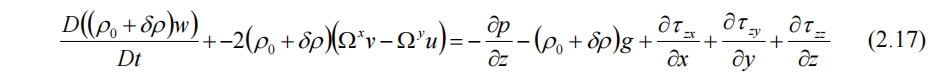
根据假设,左侧密度仍视为ρ0,而右侧不变,再忽略科氏力和粘性项,得到

对p也进行拆分,

其中p0对应静力平衡、密度为ρ0时的压力梯度,δp为密度波动导致的压力波动
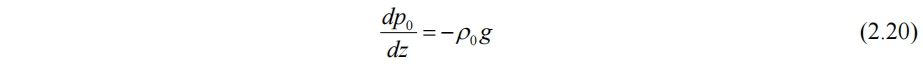
(2.19)和(2.20)带入(2.18)得

其中
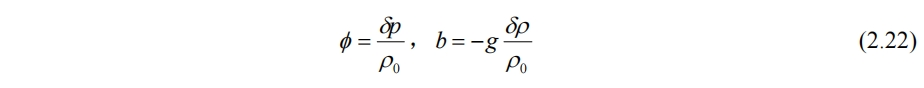
在该假设下,x方向动量方程为
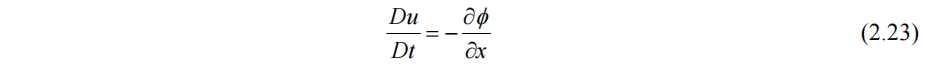
y方向同理。前有δρ<<ρ0,而式(2.22)中不忽略b的原因是g相对来说比较大(从量纲分析中也可看出),因此b未必很小,不可忽略。而b就是在布辛尼斯克假设下的浮力项,修正了纯静力平衡时浮力项缺失的问题。
浮力项密度改变的情况下,对(2.10)积分,水面压强仍认为相等且为0,得

带入(2.16)得
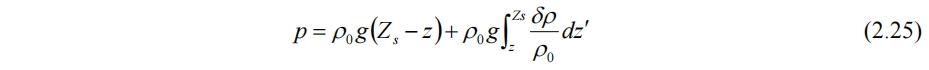
流体密度的变化量可用有效示踪剂的浓度来表示,如含盐量、含沙量等,温度也可包含在内,有

其中β为膨胀系数,为恒压下密度变化率与原密度之比

对(2.27)线性近似得

有多个量同时变化时累加即为(2.26)。
后续不考虑在竖直方向上流体密度的变化,因为一旦这样,会在静力平衡方程中引入z,使得x、y方向速度与z有关。因此认为流体在竖直方向没有密度变化,而允许在水平方向有密度变化,且仍可用膨胀系数来描述。
2.6.4 气体等效
流体密度不变时,引入单位面积密度和单位长度压力

Zs(x, y, t)为海面高度,Zb(x, y)为海底高度,不考虑海底移动的情况。(2.29)对时间的导数为

带入(2.14)得
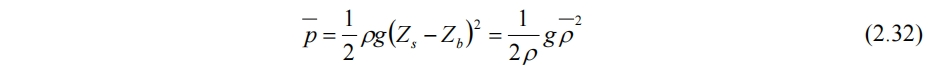
(2.32)满足绝热关系,且绝热指数γ=2。根据气体动力学声速公式可得
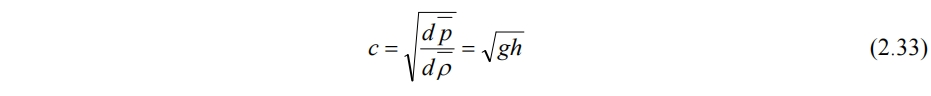
h为水深,h=Zs-Zb。
式(2.33)也可从浅水方程得到的波动方程线性化后求解特征值得出。
2.7 再看浅水近似
在(2.23)中由量纲分析有(T取L/U)

带入(2.21)得
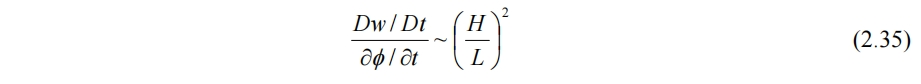
因此若要忽略z方向的加速度,满足流体静力平衡假设,就需要H<<L,这也是叫浅水方程的一个原因。另外z方向密度不变也是后续积分的前提,浅水近似也能使该假设更合理。
2.7.1 z方向密度不变
为能得到深度平均的2维浅水方程,密度在z方向的变化会破坏深度平均的简洁。因此不考虑布辛尼斯克对于竖直z方向密度的变化相关假设,而允许密度在水平xy方向有改变。此时对于式(2.10)积分得
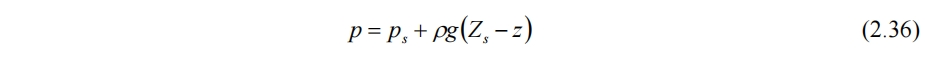
其中ps为水面大气压。对上式求x方向偏导得

y方向同理。可见其中出现了密度在x方向的导数项,如有必要可用(2.26)式带入膨胀系数具体计算。
2.7.2 z方向加速度和速度很小
由于静力平衡假设,流体在z方向认为无加速度,但这并不意味流体在z方向无速度,而是z方向速度变化很慢;更严谨应该是z方向流体的加速度与g相比非常小,即使认为z方向加速度为0,也能满足静力平衡近似得到的结果。
另外还有浅水近似、平面高度函数假设和拉格朗日假设,流体在z方向的速度必须非常小才能不破坏表面。而u、v与z无关,水深h又很小,通常可认为u、v在z方向是均匀的,但不均匀也可以,后续具体讨论。
2.8 3维浅水方程
综上,3维密度xy可变下静力平衡切平面近似的x方向动量方程为

其中ps为水面大气压力,这里认为其在xy方向也有变化。密度由前述也允许在xy方向有变化。y方向动量方程同理得
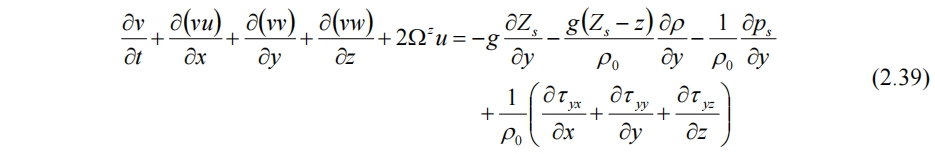
z方向动量方程已退化进xy方向。连续方程仍为(2.1)。

3 边界条件
3.1 数学
浅水方程在数学上要求,水面ζs和水底ζb光滑且没有洞,它们的运动是一个与时间有关的连续拓扑变形。还认为,水面和水底的高度能够看作x y t的函数,即
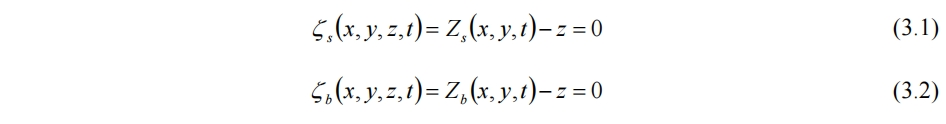
其中Zs与Zb为水面与水底的高度函数。由(3.1)可得
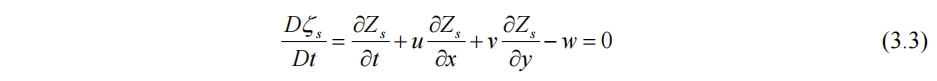
即为水面的边界条件。
若流动无旋,有速度势函数ψ满足
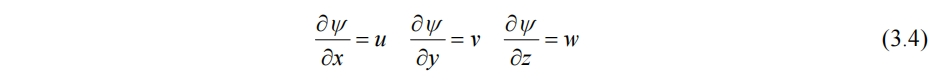
在水底速度势函数在底面法向方向的偏导应为0,即
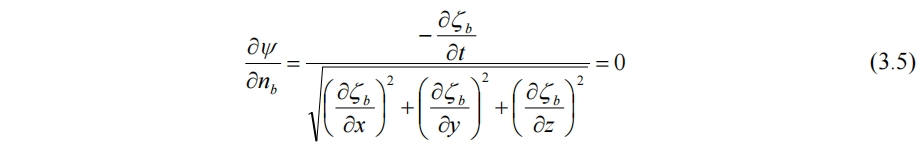
因此水底的边界条件为
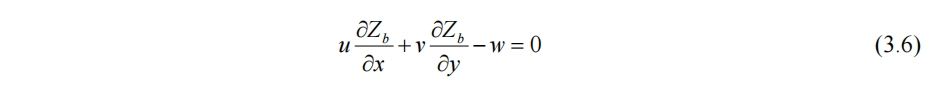
若水底可能移动,则水底边界条件与水面相同,将(3.3)式中的Zs换Zb即可。
3.2 物理
拉格朗日假设即对应3.1节数学上对水面与水底的要求。
从物理约束上看,对于不可穿透的水底,应该有流体垂直于底面方向的速度分量为0,即

其中V为流体速度矢量,而空间曲面ζ的法向量为
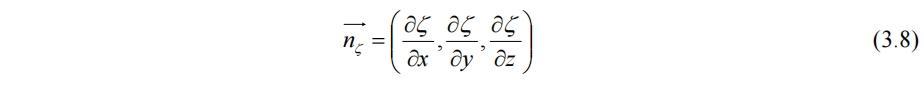
带入(3.7)即可得到(3.6)的结果。对于水底还有无滑移条件
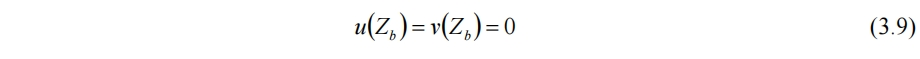
对于水面,为保证平面高度函数假设,需要使水面流体微元相对于水面的法向速度为0,即为(3.3)式。
水面的物理约束不够清晰,提供两种不够严谨(甚至错误)的“民科”思路:
3.2.1 时空速度?
空间中运动的曲面ζ(x, y, z, t)上面一点的坐标为
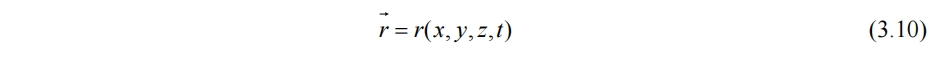
该点在时空中的速度
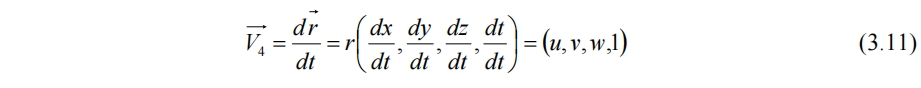
运动曲面的时空法向量

水面的相对不可穿透性有
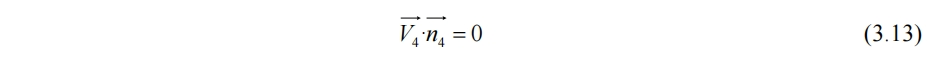
得到(3.3)的约束式。
3.2.2 表面守恒?
如果将表面流体微元的高度h=(Zs-Zb)进行积分,得到的是整个流场内流体的体积。又因为不可压缩性,质量守恒就是体积保持不变,因此该积分为定值,有

但是因为积分区域Zs在随时间变化,导数不能直接与积分交换顺序。考虑三维莱布尼茨积分法则:

其中Vs为运动表面的速度矢量由于表面并不是整个在空间平动,而是各部分有各自的速度还带弯曲,无法确定Vs。而且(3.15)式内被积分量为矢量,但h是标量,也许可以指定h方向竖直向上构造出h矢量,但后面也不知道能不能算。
感觉这种方法应该是可以,对应于控制体的积分法,只是数学不好算不来。
3.2.3 水面剪切外力?
如果有风,对表面还有剪切力约束

其中τsx为风产生的剪切力,可认为已知。(图中a为水深h,h为表面高度Zs)
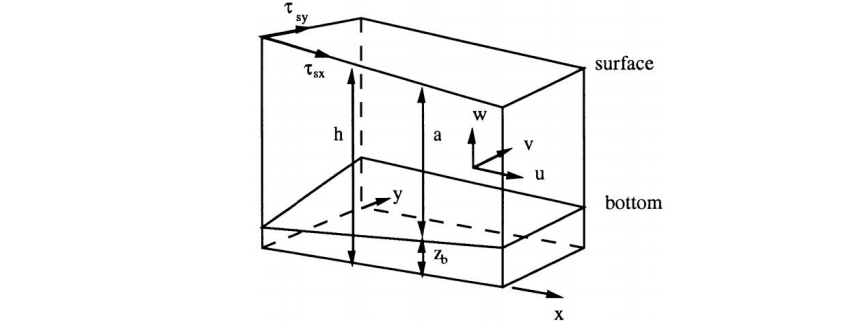
没有发现(3.16)是如何得出的。能看出右侧为微元体x平面的切应力矢量,点乘表面法向量,但是为什么它就等于风吹产生的剪切外力?
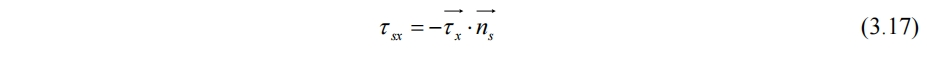

4 2维浅水方程:微分法
4.1 连续性方程
取水中任一微元控制体分析:
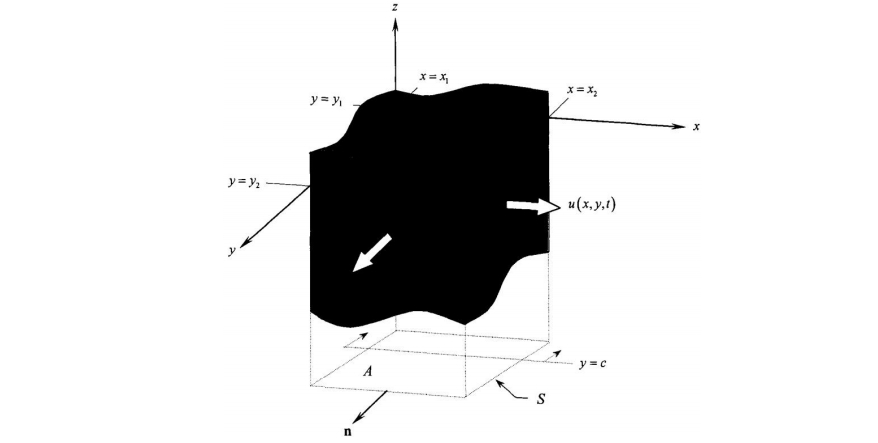
A为底面面积,S为侧面面积,n为对应面的法向量。流入为负流出为正。
4.1.1 uv在z方向均匀
单位时间内净流入控制体的质量为

其中V2=(u,v)为流体在xy平面的速度,h=Zs-Zb为水深,dl为底边线元。由格林公式

而控制体内质量变化率为

由(4.1)~(4.3)得
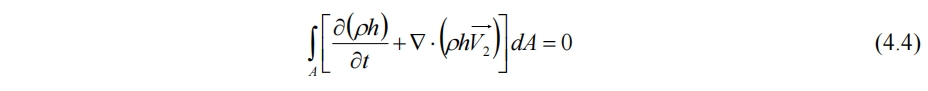
所以
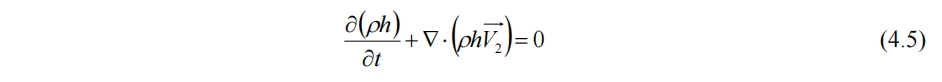
对于不可压流体,有
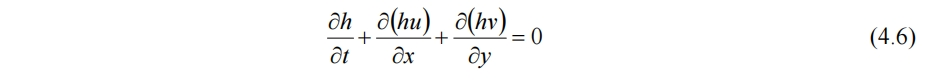
4.1.2 uv在z方向不均匀
若u和v在z方向不均匀,记深度平均速度为
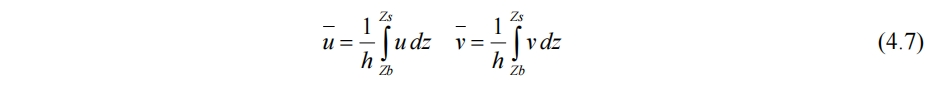
将u和v可分解为平均量和脉动量
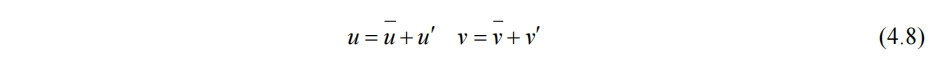
带入(4.2),应该还有一个假设,速度脉动量的积分为0,才能在积分中消去速度脉动,只剩平均值。步骤同上,不可压的结果为

4.2 动量方程,uv均匀
x方向,控制体内动量的时间变化率为

x方向受力分析如下(水面和水底仍用Zs和Zb表示,而非ζ和h;不考虑粘性力和水面力):
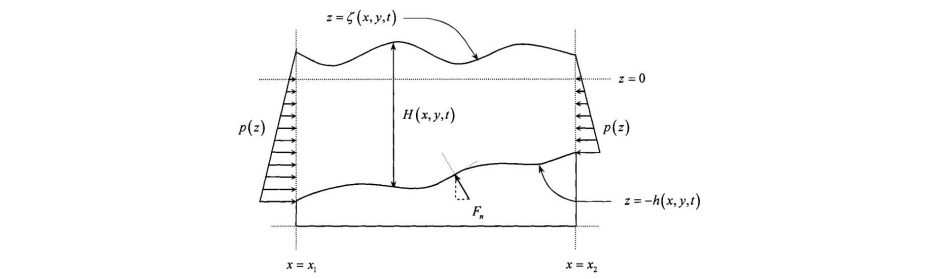
4.2.1 x方向侧压力
截面上单位宽度压力为竖直方向压力的积分,取水面压力为0,有

控制体x方向侧压力为
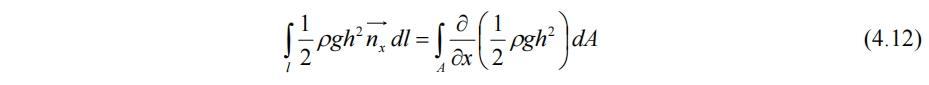
4.2.2 x方向海底力
海底对控制体的力为水压的反作用力,有
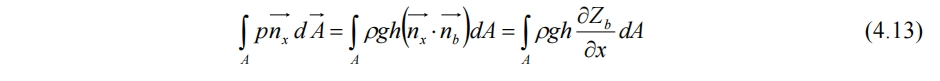
其中nb为Zb的法向量,见(3.8)式。
4.2.3 x方向流入量
x方向净流入控制体的动量为
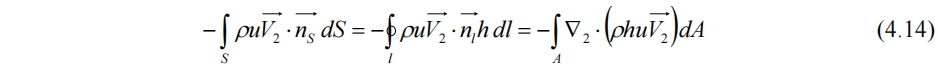
4.2.4 x方向动量方程
综上各式去掉积分号,得
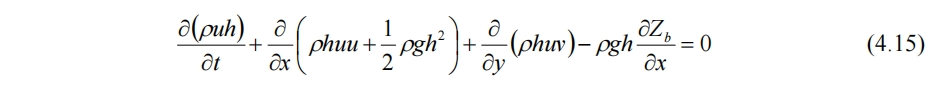
不可压时有

此即为无粘、无科氏力、无水表面力的x方向动量方程。y方向同理。
uv不均匀时同连续性方程,将平均量和脉动量替换原速度,以及脉动量积分为0的假设,应该能得出(4.16)式同样的形式,其中各速度均换成平均量。
5 2维浅水方程:积分法
5.1 连续性方程,uv均匀
积分法通过将3维浅水方程中的连续方程在z方向积分得到。对不可压缩的连续性方程(2.1)在z方向积分,有

其中
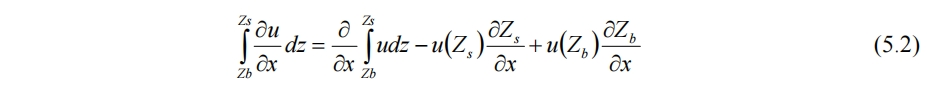
使用了莱布尼茨积分法则。第二项同理得

第三项无需使用莱布尼兹积分法则,直接积分得
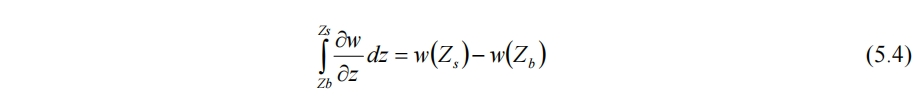
将(5.2)~(5.4)代入(5.1),结合水面和水底的边界条件(3.3)式,可得到(4.6)式。

如果uv分解为平均量和脉动量,同样假设脉动量的积分为0即可得到(4.9)式。
5.2 动量方程,uv不均匀
对3维浅水方程中的x方向动量方程(2.38)在z方向积分,有
5.2.1 非定常项

5.2.2 对流项
对流项第二项积分为

而其中
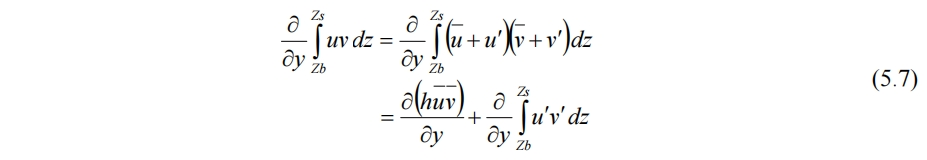
等号右侧第二项为速度空间分布不均引起的额外附加项,称微分对流项或色散项,类似雷诺应力。
对流项中第一项同理,
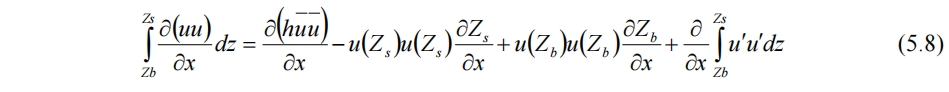
而第三项为

对流项三项之和结合水面和底面的边界条件(3.3)又可进一步化简,同(5.2)~(5.4)。
5.2.3 科氏力项
非大尺度流动情况下,纬度几乎不变,科氏力可视为常量
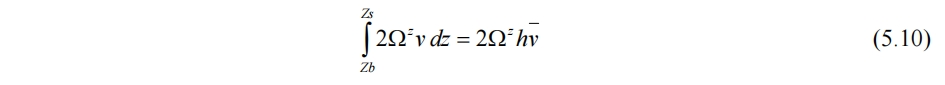
5.2.4 浮力项与大气压力项
与z无关
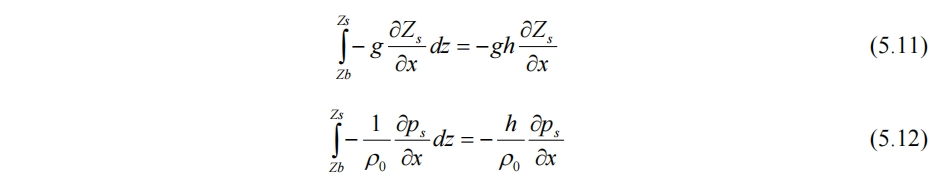
5.2.5 密度项

5.2.6 粘性项
密度倒数为常数,积分中先不考虑
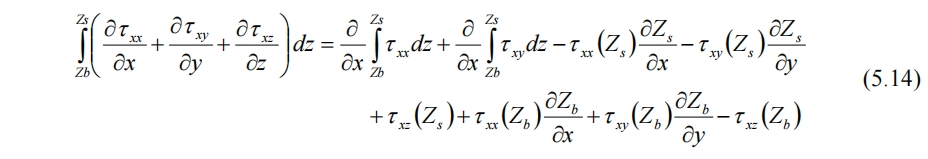
与(3.16)式类似,令
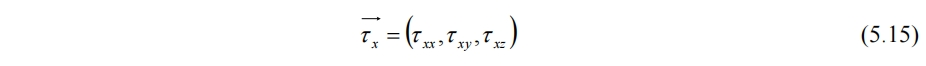
ns与nb分别为Zs与Zb的法向量,τxs与τxb为Zs与Zb面x方向的切应力,则(5.14)式可化为
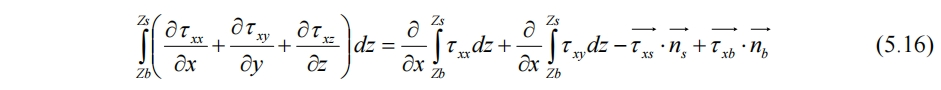
所以(3.16)式的边界条件确实是x方向的剪切力
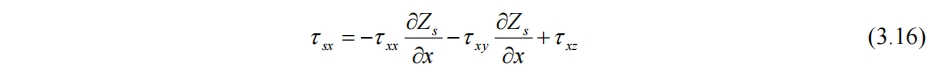
但是这是从积分结果得出的结论,而如何通过对微元体受力(有风吹提供的外部剪切力)的角度出发得出这一边界条件?
5.2.7 源项
由于认为z方向无外力,故如果有外力,任何xy方向的外力均可直接积分
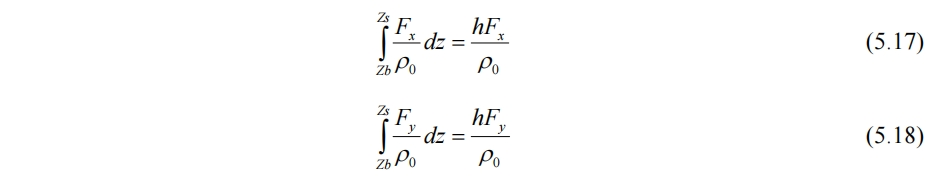
5.2.8 综合
将以上积分结果对应原动量方程位置替换,即可得到动量方程。
5.3 2维浅水方程
连续性方程由(4.6)给出
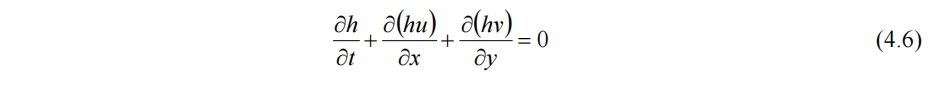
动量方程为
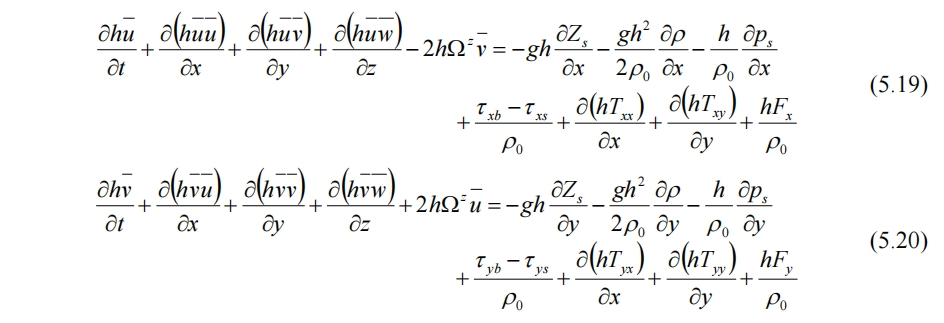
其中
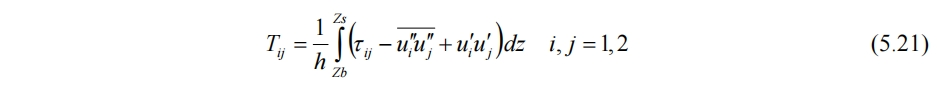
而(5.21)式中的τij又可由(1.8)和(1.9)给出。(5.21)式中还包含雷诺应力项,可认为是在(1.2)~(1.4)式进行了时间平均后进行的后续浅水方程推导。整体流程不受影响,只是粘性应力项的公式(1.8)和(1.9)中需要额外增加雷诺应力项。而在最后的(5.19)和(5.20)式中,雷诺应力项被放入了Tij里。
记
浅水方程介绍完毕,现在能把“引”中的文字渲染成画面吗?
浅水方程不觉浅,曾是惊鸿照影来。惊鸿不仅是游戏、影视作品中水面映出的惊艳角色,也是在探索流体性质乃至世界奥秘道路上无数的前辈。他们的成果并未消散,而是化作天上的星星璀璨世间,也算飞升星域了吧。而游戏,一定是科学与艺术、理性与感性最前沿、最成熟的曼妙融合。它的价值还远未被发掘完全。

惊鸿一面
做水体模拟真需要搞这些物理公式吗?显然并不需要。虽然行星级流动可能需要含科氏力的NS方程,但也如概述中所说,流体模拟与计算流体力学最根本的差别在于目的不同。算力时间有限,对游戏和影视用极高精度的仿真是一种不必要的浪费。如文明6(Civilization VI, Firaxis Games 2016)的海洋和河流模拟大概率是非物理的,这丝毫不影响游戏内容。而一些简化到不能再简化甚至从本质上说是错误的模型,却可能在水体模拟领域内有奇效。

Fournier和Reeves对此一针见血地评论道:
"We do not expect any 'physical' answer from our model. In fact, we do not ask any question except 'does it look like the real thing'. So a model which might be useless to an oceanographer might turn out to be good for our purposes. By the same token, we will feel free to adjust coefficients to achieve the needed effect, even if we are not quite sure if doing so has a physical meaning. This is of course extremely bad form when building physical models."
自己直言“糟糕的物理模型”恰好是对费米批评戴森直截了当的回应。而“随心所欲调整系数”这一点又精准踩在费米雷点上——序中费米与戴森的谈话还有后续:
Fermi asked him(Dyson) how many free parameters he had used to obtain the fit.
Smiling after being told "Four," Fermi remarked,
"I remember my old friend Johnny von Neumann used to say, with four parameters I can fit an elephant, and with five I can make him wiggle his trunk."
用四个参数冯·诺依曼都能拟合一个大象,再多给1个参数能让大象鼻子扭起来,你们水体模拟又用了多少个参数呢?当然还是因为两者目的不同,无关对错。
但以上“复杂”的浅水方程真的正确吗?注意在浅水方程的简化里有一个关键假设,是海面高度能被视为x、y、t的函数。这意味在一个确定的x、y、t下,海面高度唯一确定。但显然海浪卷起的情况就不是这样,Fournier和Reeves还使用神奈川冲浪里来形象地说明这一点(想必FGO玩家对于这张图不会陌生)。而这不仅仅是浅水方程的假设,很多其他方法也采用了这一假设。所以是复杂的模型也不一定正确,还是以上的模型远不够复杂?
就浅水方程而言以上也只是入门,还有很多内容如旋度势守恒、能量方程、线性非线性浅水波等根本看不懂,非专业方向,上述内容也几乎一定有错误的地方。为了学习这些入门内容已经好几天没开过steam。有兴趣的玩家可以继续深入探究。
打游戏去了。
尾
“夏,你知道吗?
这世上的路有许多条,
每个人都有属于自己的那条。”
参考
[1] 《十日终焉》, 杀虫队队员
[2] Jeff Bezos, 偏微分方程:浇灭了杰夫·贝索斯的物理梦
[3] Segre G., Hoerlin B. The Pope of Physics: Enrico Fermi and the Birth of the Atomic Age.
[4] Mehra J., Rechenberg H. The historical development of Quantum Theory
[5] 王洪伟, 我所理解的流体力学
[6] 陈懋章, 粘性流体力学基础
[7] 刘沛清, 空气动力学
[8] Wilcox D C .Turbulence Modeling for CFD
[9] Lamb S H .Hydrodynamics
[10] De-Leon Y, Linear waves in midlatitudes on the rotating spherical earth.
[11] J.J. Stoker. Water waves: the Mathematical Theory with Applications
[12] Arakawa, A. Computational design for long-term numerical integration of the equations for fluid motion: two-dimensional incompressible flow
[13] Heaps, N.S. Three-dimensional coastal ocean models
[14] Wubs, F.W. Numerical solution of the shallow-water equations
[15] Peachey D R .Modeling waves and surf
[16] Fedotova Z I , Khakimzyanov G S .Nonlinear dispersive equations of the shallow water on the rotating sphere
[17] Paldor N. Shallow Water Waves on the Rotating Earth
[18] Vreugdenhil C. B. Numerical Methods for Shallow-Water Flow
[19] Bates P. D. A New Method for Moving-Boundary Hydrodynamic Problems in Shallow Water.
[20] Li B., Fleming C., Three-dimensional Model of Navier-Stokes Equations for Water Waves.
[21] Vallis G K .Essentials of Atmospheric and Oceanic Dynamics
[22] Khakimzyanov G S Dispersive Shallow Water Waves: Theory, Modeling, and Numerical Methods
[23] Kubatko E .Development, implementation, and verification of hp discontinuous Galerkin models for shallow water hydrodynamics and transport.
[24] Fournier A , Reeves W T .A Simple Model of Ocean Waves.
[25] D.R. Lynch, A wave equation model for finite element tidal computations
[26] A. Oliveiria, Mass balance in Eulerian-Lagrangian transport simulations in estuaries
[27] University O .Waves, Tides & Shallow-Water Processes
[28] Deutsch.The Shallow Water Wave Equations: Formulation, Analysis and Application
[29] Roe, P. L. , Upwind Schemes Using Various Formulations of the Euler Equations, Numerical Methods for the Euler Equations of Fluid Dynamics
[30] Ouazar, D. , Computer Methods and Water Resources