
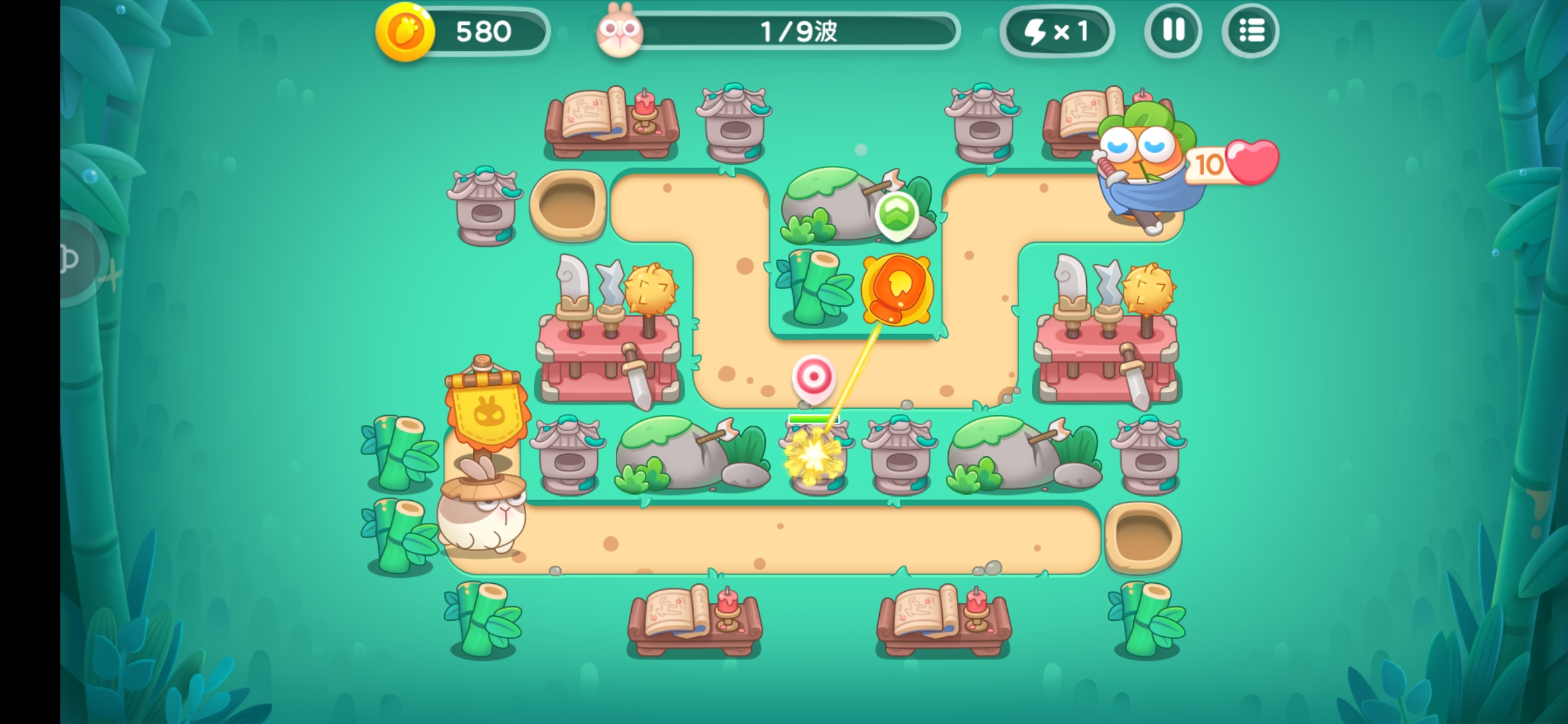
↑ ↑ ↑ 火瓶子 ↑ ↑ ↑
------分割線------
Part1:對建築物的攻擊範圍
1.算法分析:
鑑於建築物為靜態存在,我們可以近似地使用Dijkstra算法來判定攻擊範圍。Dijkstra算法是從一個頂點到其餘各頂點的最短路徑算法,解決的是有權圖中最短路徑問題,主要特點是從起始點開始,採用貪心算法的策略,每次遍歷到始點距離最近且未訪問過的頂點的鄰接節點,直到擴展到終點為止。
每一個地圖,可以看成一個已知大小的二維矩陣,只要確定了中心點(塔的位置),然後向上下左右四個方向展開搜索,規定中心點的數值為0,下一個格子的數值為本格子的數值加1。對於地圖上的每一個格子,算出到達這個格子的最短路徑,最終遍歷完所有的格子之後,獲得最短的路線。
2.實例演示:
↓ ↓ ↓ 一級火瓶子 ↓ ↓ ↓


↓ ↓ ↓ 二級火瓶子 ↓ ↓ ↓

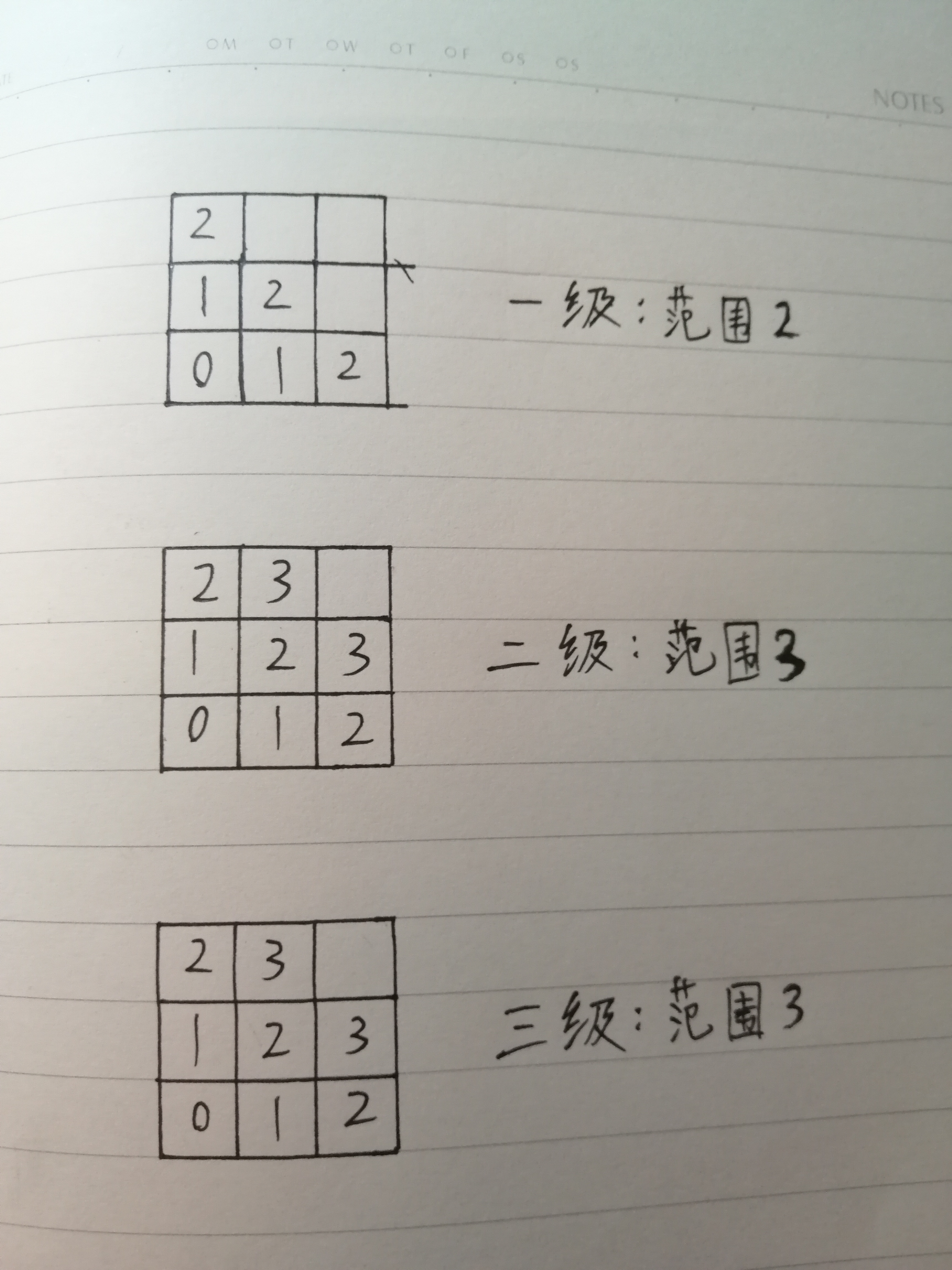
↓ ↓ ↓ 三級火瓶子 ↓ ↓ ↓


3.建模總結:
限定直線 y=0 和 y=x 在第一象限所圍成的區域(含邊界),各等級火瓶子有以下攻擊範圍。一級火瓶子:(1,0),(1,1),(2,0)。二級火瓶子:(1,0),(1,1),(2,0),(2,1)。三級火瓶子:(1,0),(1,1),(2,0),(2,1)。
Part2:對兔子的攻擊範圍
1.算法分析:
由於兔子會在路徑上勻速移動,我們可以使用碰撞檢測算法來判定攻擊範圍。碰撞檢測是建立在碰撞體上的,而碰撞體是對一個物體“邊界”的確切描述。它描述了每個需要進行碰撞檢測的物體的邊界,並依靠數學方法判斷這些邊界是否相交,進而產生碰撞檢測的結果。
兔子的碰撞體可近似看成一個圓(或者是一個圓角的正方形),火瓶子的攻擊範圍也是一個圓,恰好構成了最簡單的一類碰撞體——圓形碰撞體。根據初中數學的勾股定理,以及兩圓相交的判定定理,即可獲取其有效的攻擊範圍。
2.實例演示:
↓ ↓ ↓ 一級火瓶子 ↓ ↓ ↓

↓ ↓ ↓ 二級火瓶子 ↓ ↓ ↓

↓ ↓ ↓ 三級火瓶子 ↓ ↓ ↓

↓ ↓ ↓ 2D碰撞檢測 ↓ ↓ ↓
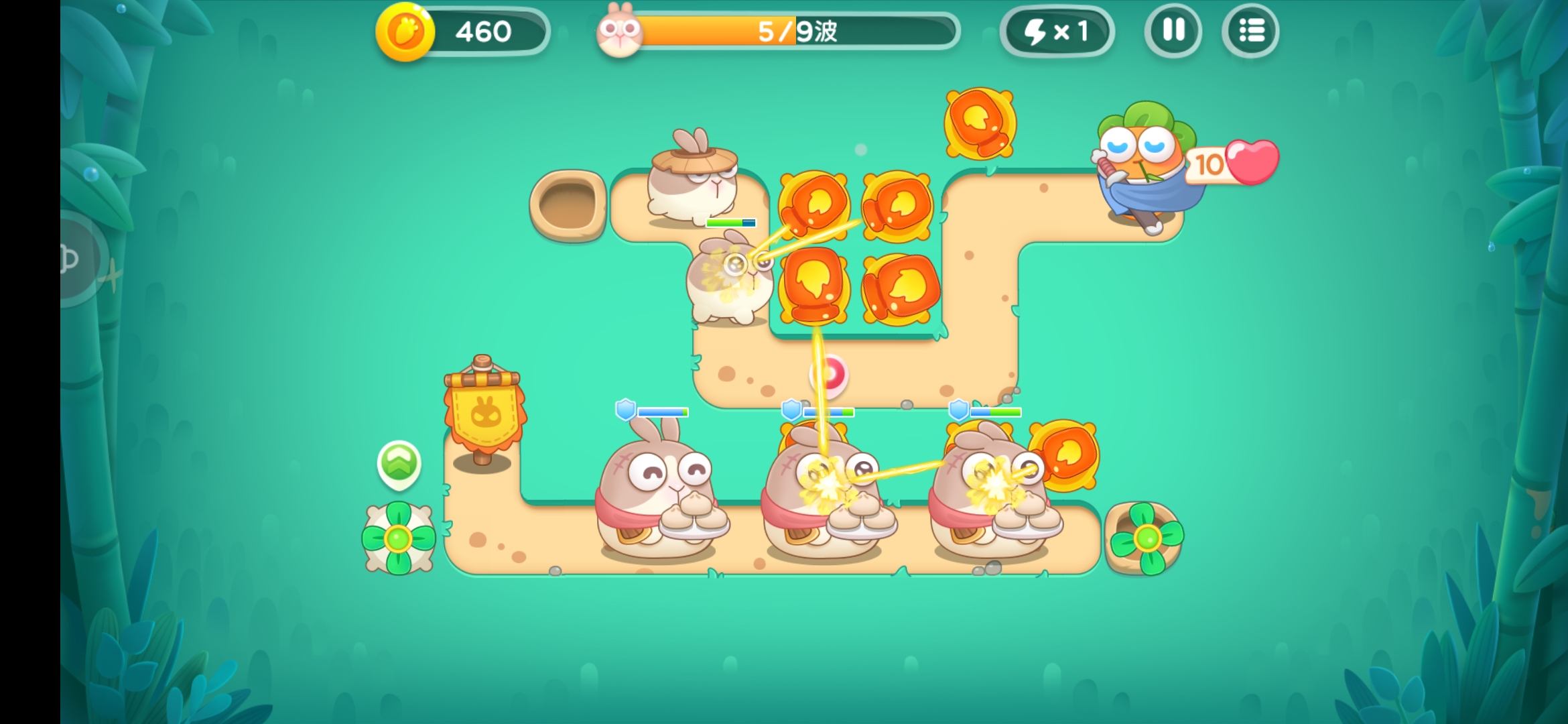
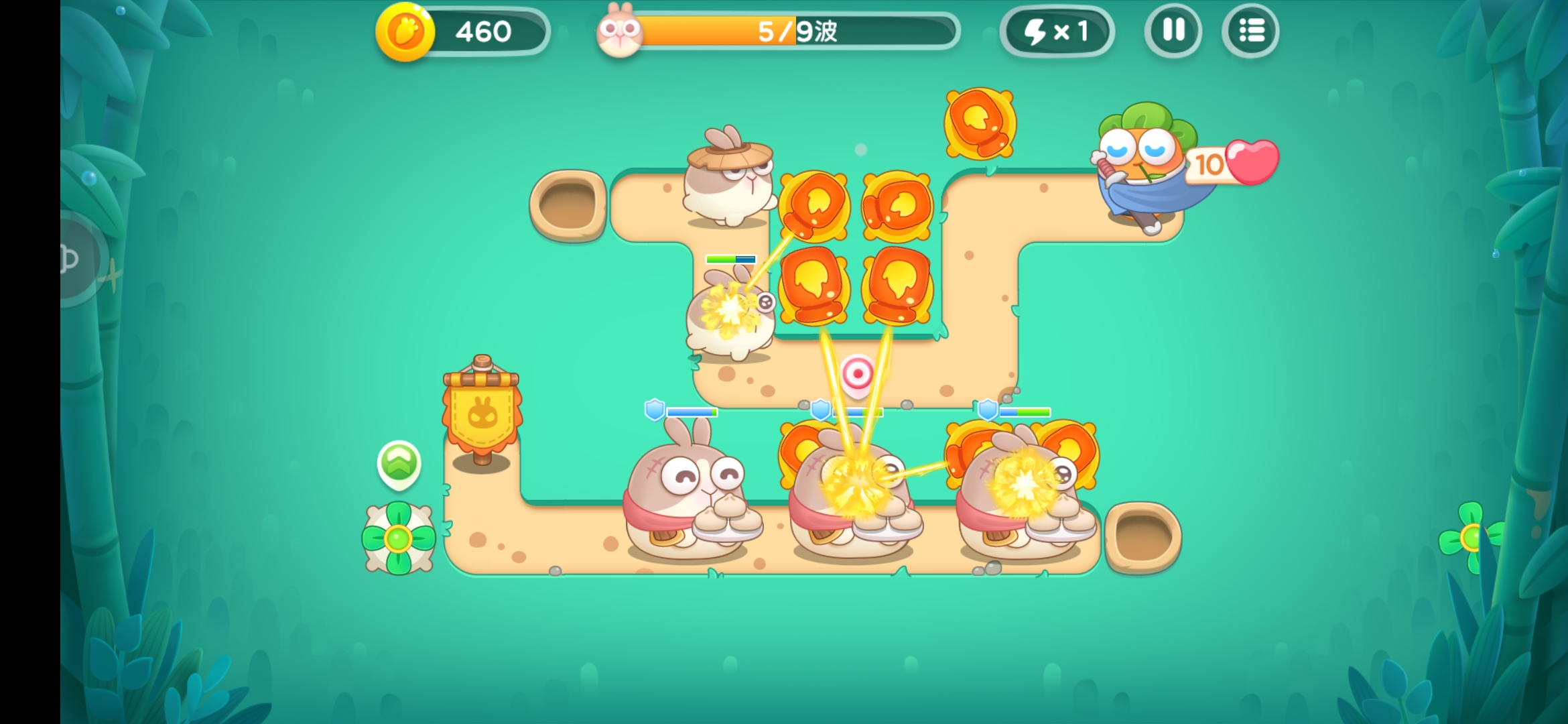
↓ ↓ ↓ 巨呆兔和呆萌兔的對比 ↓ ↓ ↓
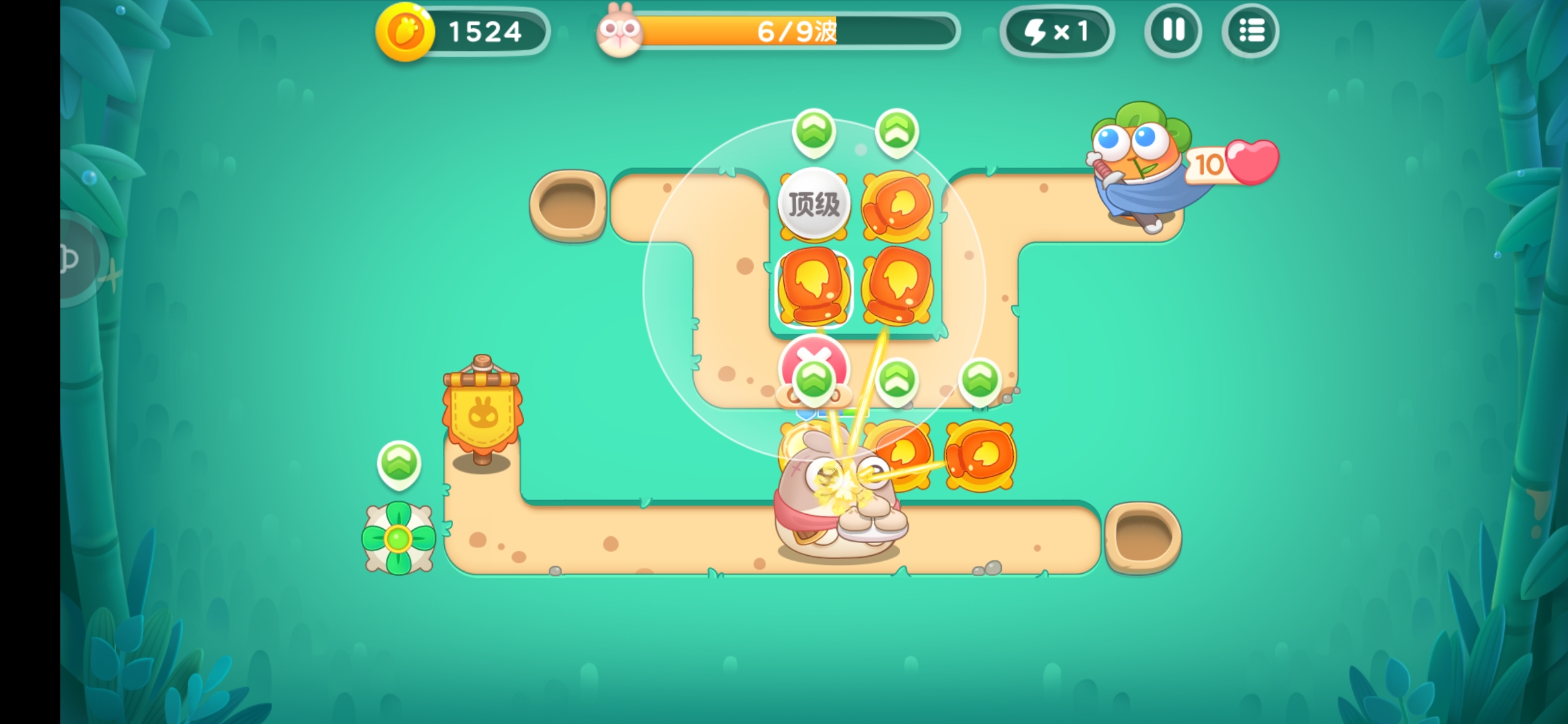
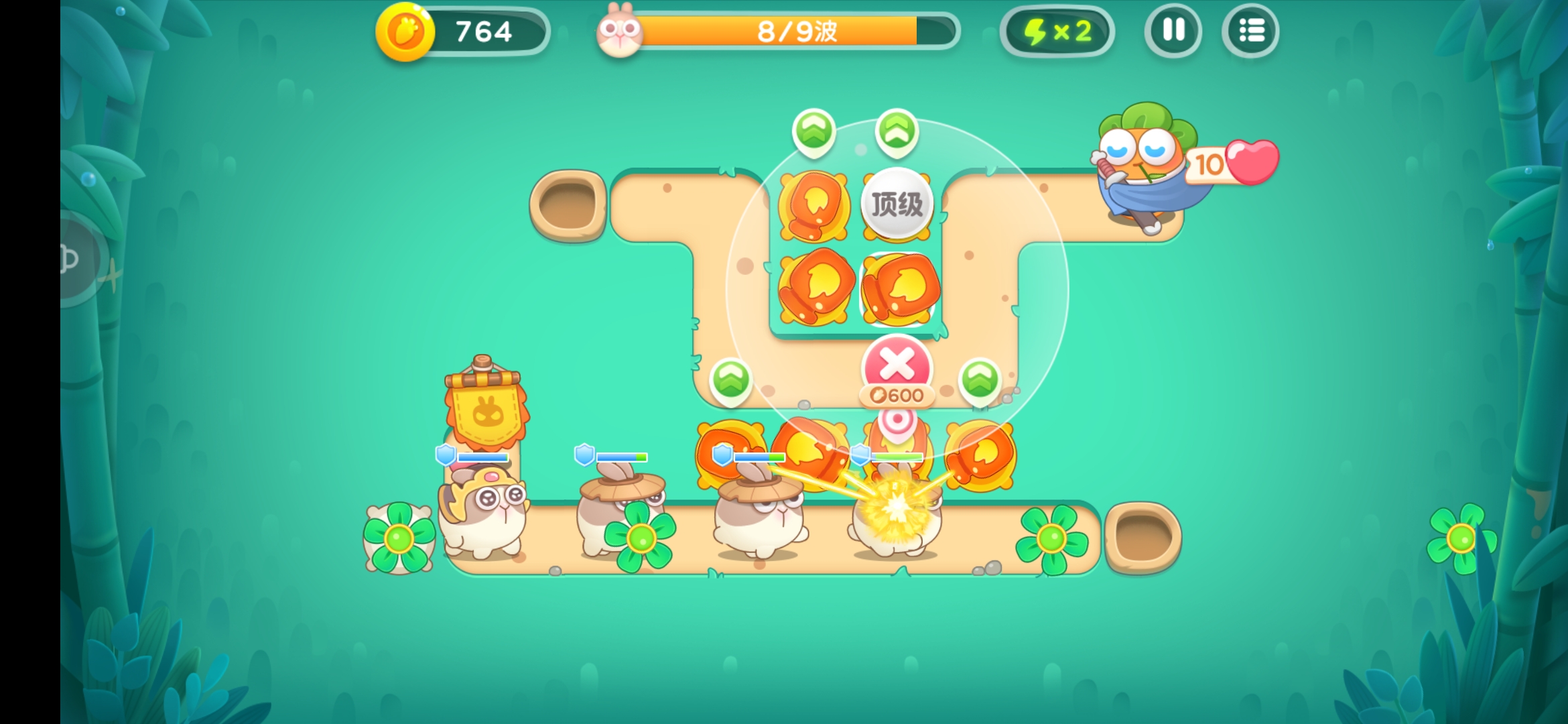
↓ ↓ ↓ 模型高度對比 ↓ ↓ ↓
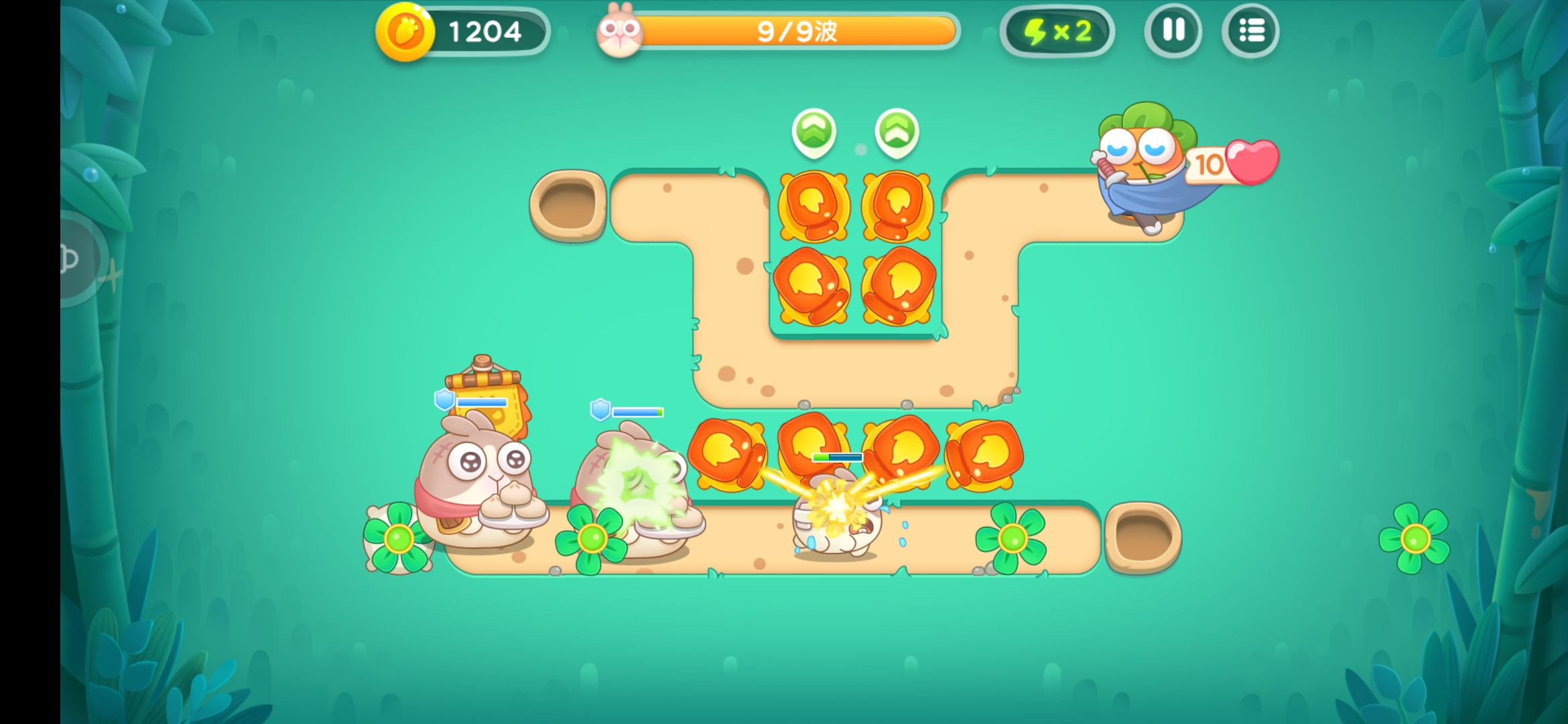
3.建模總結
圓形碰撞體擁有最簡單的計算過程,在運動速度夠快(或形狀夠圓)的情況下也不會有太大的違和感,所以這種碰撞體在彈幕遊戲和塔防遊戲中應用廣泛。對於巨呆兔而言,它所在的路徑 並不在火瓶子的攻擊範圍內,但它的2D模型中心點卻在路徑上方,且其半徑比呆萌兔的模型半徑大,所以火瓶子完成了“不可能”做到的降維打擊,呆萌兔幸運地逃過一劫(笑)。

------分割線------
如果有小夥伴對本文感到疑惑,或者想與樓主作進一步的探討,歡迎在評論區留言哦~