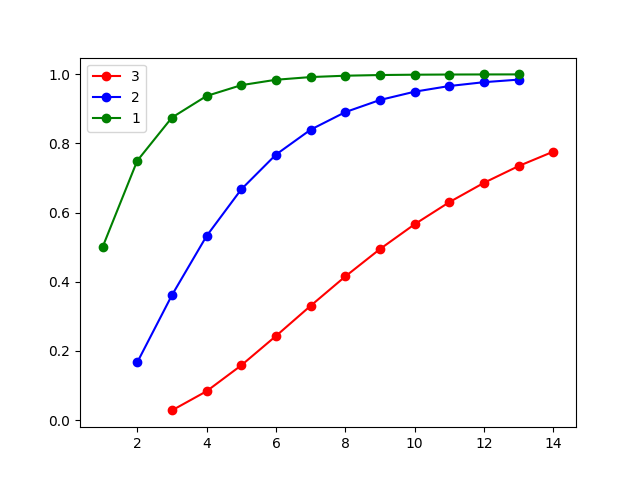
横坐标是出五星刻印的n次数，纵坐标是y概率，321分别指刷出x个合适刻印。合起来就是n次内刷出来x个刻印的概率y。x实际上横坐标超过7就没意义了
。然后就是不需要算就可以得出的结论：是欧狗就3%的概率3次出货，运气一般就5次出货，实在倒霉就7次拿大保底。一般人刷二换一就行了，刷一换二也不是不行，毕竟狗粮那么缺。
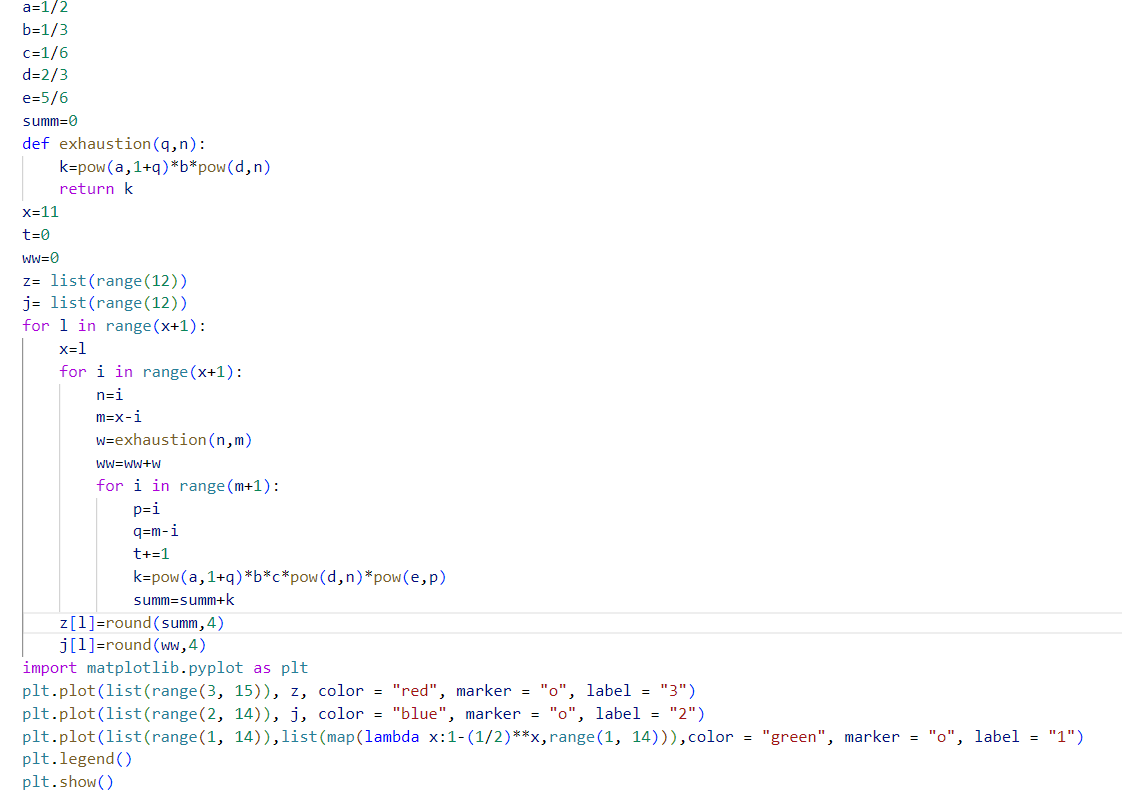先是套娃穷举，加到一起放到数组里再作图希望没算错
。a=1/2
b=1/3
c=1/6
d=2/3
e=5/6
summ=0
def exhaustion(q,n):
k=pow(a,1+q)*b*pow(d,n)
return k
x=11
t=0
ww=0
z= list(range(12))
j= list(range(12))
for l in range(x+1):
x=l
for i in range(x+1):
n=i
m=x-i
w=exhaustion(n,m)
ww=ww+w
for i in range(m+1):
p=i
q=m-i
t+=1
k=pow(a,1+q)*b*c*pow(d,n)*pow(e,p)
summ=summ+k
z[l]=round(summ,4)
j[l]=round(ww,4)
import matplotlib.pyplot as plt
plt.plot(list(range(3, 15)), z, color = "red", marker = "o", label = "3")
plt.plot(list(range(2, 14)), j, color = "blue", marker = "o", label = "2")
plt.plot(list(range(1, 14)),list(map(lambda x:1-(1/2)**x,range(1, 14))),color = "green", marker = "o", label = "1")
plt.legend()
plt.show()